Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark

Abstract Previous lecture Next lecture Index References Contents

In this lecture we first introduce the main programming paradigms. Next we introduce the functional programming paradigm using the programming language Scheme. In this lecture We cover expressions, types, lists, definitions, and the basic function concept. A number of examples are given, when possible from the web domain. The introduction to the paradigm and Scheme is continued in the next lecture which covers name binding, recursion and iteration.

Lisp is the next oldest programming language - only Fortran is older.

Lisp characteristics: Invented for symbolic computations Superficially inspired by mathematical function theory Is syntactically and uniformly based on parenthesized prefix notation Parsing a Lisp program is trivial Programming goes hand in hand with language development It is easy to access and manipulate programs from programs Calls for tool making in Lisp

References Foldoc: Lisp Foldoc: prefix notation

Program = Data = Lists

Scheme Slide Annotated slide Contents Index References Textbook

Scheme is a small, yet powerful language in the Lisp family

Scheme characteristics: Supports functional programming - but not on an exclusive basis Functions are first class data objects Uses static binding of free names in procedures and functions Types are checked and handled at run time - no static type checking Parameters are evaluated before being passed - no lazyness

Scheme is an attractive alternative to Common Lisp (a big monster) and Emacs Lisp (the rather primitive extension language of the Emacs text editor).

References Schemers.org home page The Scheme Language Report Foldoc: Scheme

Exercise 2.2. Getting started with Scheme and LAML

The purpose of this exercises is learn the most important practical details of using a Scheme system on Unix. In case you insist to use Windows we will assume that you install the necessary software in your spare time. There is no time available to do that during the course exercises. Further details on installation of Scheme and LAML on Windows. You will have to choose between DrScheme and MzScheme. DrScheme is a user friendly environment for creating and running Scheme programs, with lots of menus and lots of help. However, it is somewhat awkward to use DrScheme with LAML. Only use DrScheme in this course if you cannot use Emacs, or if you are afraid of textually, command based tools. Follow this link for further details. MzScheme is the underlying engine of DrScheme. MzScheme is a simple read-eval-print loop, which let you enter an expression, evaluate and print the result. MzScheme is not very good for debugging and error tracing. MzScheme works well together with Emacs, and there is a nice connection between MzScheme and LAML. MzScheme used with Emacs is preferred on this course. Please go through the following steps: Insert the following line in your .emacs file in your home dir, and then restart Emacs: (load "/pack/laml/emacs-support/dot-emacs-contribution.el") Have a session with a naked Scheme system by issuing the following command in Emacs: M-x run-scheme-interactively Define a couple of simple functions ( odd and even, for instance) and call them. Split the window in two parts with C-x 2 and make a buffer in the topmost one named sources.scm ( C-x b ). Bring the Scheme interpreter started above into the lower part of the window. The buffer with the Scheme process is called *inferior-lisp*. Put the sources.scm buffer in Scheme mode ( M-x scheme-mode ). Define the functions odd and even in the buffer and use the Scheme menu (or the keyboard shortcuts) to define them in the running Scheme process. Have a similar session with a Scheme+LAML system by issuing the following command in Emacs: M-x run-laml-interactively (You may have to confirm that a previously started Scheme process is allowed to be killed). All you did in item 2 can also be done here. Evaluate a simple HTML expression, such as (html (head (title "A title")) (body (p "A body"))) Use the function xml-render to make a textual rendering of the HTML expression. Make a deliberate grammatical error in the LAML expression and find out what happens. Make a file 'try.laml'. Control that Emacs brings the buffer in Laml mode. Issue a M-x laml-mode explicitly, if necessary. Use the menu 'Laml > Insert LAML template' to insert an XHTML template. Fill in some details in the head and body. Process the file via the LAML menu in Emacs: Process asynchronously. The file try.html will be defined. Play with simple changes to the HTML expression, and re-process. You can just hit C-o on the keyboard for processing. You can get good inspiration from the tutorial Getting started with LAML at this point.

Evaluation of an expression yields a value which belongs to a type

Expressions Written by the programmer Will typically involve one or more function calls A Function - as written by the programmer - is itself an expression Values Primitive as well as composite A function expression is evaluated to a function object Types A set of values with common properties Type checking can be used to validate a program for certain errors before it is executed Expressions are part of the source program, as written by the programmer. A function expression is called a lambda expression. We will encounter these important expressions later in this material. The primitive values are those which cannot be decomposed into more primitive parts. Some of the important primitive values are numbers, the two boolean values (true and false), and the characters of some character set. Primitive values stand as a contrast to composite values, such as lists and arrays, which are aggregations of parts, each of which are compositive or primitive values themselves.

Examples of expressions and their values Slide Annotated slide Contents Index References Textbook

Let us assume that x has the value 3 Simple expressions 7    has the value 7 (+ x 5)    has the value 8 Conditional expressions (if (even? x) 7 (+ x 5))    has the value 8 Lambda expressions (lambda (x) (+ x 1))    has the value 'the function that adds one to its parameter' HTML mirror expressions (html (head (title "PP")) (body (p "A body paragraph")) ) The value of this expression can be rendered as a string in HTML which can be presented in an Internet browser. The conditional expression is evaluated in two steps. First the boolean expression (even? x) is evaluated. If x is even, the boolean expression (even? x) evaluates to true and the trivial expression 7 is evaluated. Because x is 3 and therefore odd, the other expression (+ x 5) is evaluated, giving us the final value 8. It is important to realize that an if form does not evaluate all three constituent expressions at the outset. It first evaluates the boolean expression, and based on the outcome, it either evaluates the 'then part' or the 'else part'. Not both! We have much more to say about the order of evaluation of an if form in a later part of this material Regarding the lambda expression, the x in parentheses after lambda is the formal parameter of the function. the expression (+ x 1) is the body. In functions, the body is an expression - not a command. The HTML mirror expressions stem from the LAML libraries. The functions html, body, title, head, and p correspond to the HTML elements of the same names. In the LAML software, the HTML elements are mirrored as functions in Scheme.

This material includes a lecture that explains the important and relevant details about LAML. Not least, this lecture explains the calling conventions of the so-called HTML mirror functions.

LAML and HTML mirror functions

Reference Conditional expressions and the order of evaluation

Evaluation of parenthesized expressions Slide Annotated slide Contents Index References Textbook

Here we will emphasize the rules of evaluating a form like (a b c d e) in Scheme

How is the form (a b c d e) evaluated in Scheme? The form (a b c d e) appears as a pair of parentheses with a number of entities inside. The question is how the parenthesized expression is evaluated, and which constraints apply to the evaluation.

Evaluation rules The evaluation of the empty pair of parentheses ( ) is in principle an error If a is the name of a special form, such as lambda, if, cond, or define special rules apply In all other cases: Evaluate all subforms uniformly and recursively. The value of the first constituent a must be a function object. The function object is called with the values of b, c, d, and e as actual parameters. The evaluation of the empty pair of parentheses ( ) is often - in concrete Scheme systems - considered as the same as '( ), which returns the empty list. However, you should always quote the empty pair of parentheses to denote the empty list.

References R5RS: Procedure calls Beta Reduction - calling a function

Arithmetic expressions Slide Annotated slide Contents Index References Textbook

We will here point out that arithmetic expressions are written as fully parenthesized expressions with prefix notation

Scheme uses fully parenthesized arithmetic expressions with prefix notation

The concept prefix notation: Using prefix notation the operator is given before the operands

Prefix notation stands as a contrast to infix and postfix notation. Infix notation is 'standard notation' in which the operand is found in between the operands.

Table. Examples of arithmetic expressions. The prefix notation can be seen to the left, and the values of the expressions appear to the right.

Expression Value (+ 4 (* 5 6)) 34 (define x 6) (+ (* 5 x x) (* 4 x) 3) 207 (/ 21 5) 21/5 (/ 21.0 5) 4.2 (define (fak n) (if (= n 0) 1 (* n (fak (- n 1))))) (fak 50) 30414093201713378043612608166064768 844377641568960512000000000000

There is no need for priorities - operator precedence rules - of operators in fully parenthesized expressions

References R5RS: Numbers in Scheme R5RS: Numerical operations

Reference Foldoc: prefix notation

Equality in Scheme Slide Annotated slide Contents Index References Textbook

On this page we will discuss equality functions in Scheme

As most other programming languages, Scheme supports a number of different equivalence predicates

The most discriminating eq? The least discriminating - structural equivalence equal? Exact numerical equality = Others eqv? is close to eq? string=? is structural equivalence on strings

Program: A sample interaction using and demonstrating the equivalence functions in Scheme.

1> (eq? (list 'a 'b) (list 'a 'b)) #f 2> (eqv? (list 'a 'b) (list 'a 'b)) #f 3> (equal? (list 'a 'b) (list 'a 'b)) #t 4> (= (list 'a 'b) (list 'a 'b)) =: expects type <number> as 2nd argument, given: (a b); other arguments were: (a b) 5> (string=? "abe" "abe") #t 6> (equal? "abe" "abe") #t 7> (eq? "abe" "abe") #f 8> (eqv? "abe" "abe") #f

Reference Equivalence predicates in R5RS

The read-eval-print loop Slide Annotated slide Contents Index References Textbook

On this page we will explain the idea and virtues of the so-called read-eval-print loop of Lisp and Scheme systems.

The 'read-eval-print loop' allows you to interact with a Scheme system in terms of evaluation of individual expressions Some authors talk about a REPL - Read Eval Print Loop.

Program: A sample session with Scheme using a read eval print loop.

1> (+ 4 (* 5 6)) 34 2> (define x 6) 3> (+ (* 5 x x) (* 4 x) 3) 207 4> (/ 21 5) 21/5 5> (/ 21.0 5) 4.2 6> (define (fak n) (if (= n 0) 1 (* n (fak (- n 1))))) 7> (fak 50) 30414093201713378043612608166064768844377641568960512000000000000

The notion of type is used to make programs more readable, make them run more efficient, and to detect certain errors before they cause errors in the calculation.

Readability Explicitly typed variables, parameters and function serve as important documentation, which enhances the program understanding. Efficiency Knowledge of the properties of data makes it possible to generate more efficient code Correctness Explicit information about types in a program is a kind of redundancy against which it is possible to check expressions and values Programmers usually wish to identify type errors as early as possible in the development process

Reference Foldoc: type

Type checking Slide Annotated slide Contents Index References Textbook

As already mentioned the use of types in source programs makes it possible to deal with program correctness - at least in some simple sense. In this context, correctness is not relative to the overall intention or specification of the program. Rather, it is in relation to the legal use of values as input to operators and functions.

Type checking is the processes of identifying errors in a program based on explicitly or implicitly stated type information

Weak typing Type errors can lead to erroneous calculations Strong typing Type errors cannot cause erroneous calculations The type check is done at compile time or run time Static typing The types of all expressions are determined before the program is executed The type check is typically carried out in an early phase of the compilation Comes in two flavors: explicit type decoration and implicit type inference Static typing implies strong typing According to section 1.1 the Scheme Report (R5RS) 'Scheme has latent as opposed to manifest types. Types are associated with values (also called objects) rather than with variables.' In our categorization, Scheme is strongly typed and types are dealt with at run time (on values) as a contrast to compile time (on variables).

Reference R5RS: Semantics (Types in Scheme)

References Foldoc: strong typing Foldoc: weak typing

Static type checking Slide Annotated slide Contents Index References Textbook

We here make the distinction between explicit type decoration and implicit type inference, and explain the principled difference.

There are two main kinds of static type checking: explicit type decoration and implicit type inference

Eksempel. Let us study the expression (+ x (string-length y))

 

Explicit type decoration Variables, parameters, and others are explicitly declared of a given type in the source program It is checked that y is a string and that x is a number Implicit type inference Variables and parameters are not decorated with type information By studying the body of string-length it is concluded that y must be a string and that the type of (string-length y) has to be an integer Because + adds numbers, it is concluded that x must be a number

An example of type checking Slide Annotated slide Contents Index References Textbook

Is the expression   (+ 1 (if (even? x) 5 "five"))   correct with respect to types? The example shows an arithmetic expression that will cause a type error with most type checkers. However, if x is even the sum can be evaluated to 6. If x is odd, we encounter a type error because we cannot add the integer 1 to the string "five".

Weak typing It is not realized that the expression (+ 1 "five") is illegal. We can imagine that it returns the erroneous value 47 Strong typing If, for instance, x is 2, the expression (+ 1 (if (even? x) 5 "five")) is OK, and has the value 6 If x is odd, it is necessary to identify this as a problem which must be reported before an evaluation of the expression is attempted Static typing (+ 1 (if (even x) 5 "five"))   fails to pass the type check, because the type of the expression cannot be statically determined Static type checking is rather conservative

Types in functional programming languages Slide Annotated slide Contents Index References Textbook

Before we proceed we will compare the handling of types in Scheme with the handling of types in other functional programming languages. Specifically, we compare with Haskell and ML.

Scheme is not representative for the handling of types in most contemporary functional programming languages

ML and Haskell Uses static typing ala implicit type inference Some meaningful programs cannot make their way through the type checker There will be no type related surprises at run time Scheme Is strongly typed with late reporting of errors Type errors in branches of the program, which are never executed, do not prevent program execution There may be corners of the program which eventually causes type problems

Due to the handling of types, Scheme and Lisp are elastic and flexible compared with ML, Haskell, and other similar language which are quite stiff and rigid.

A list is recursively composed of a head and a tail, which is a (possibly empty) list itself The building blocks of lists are the cons cells Every such cell is allocated by an activation of the cons function

An illustration list construction and list selection. We first construct a list (d c b a) and we bind it to the variable lst. Next we select the first element, the tail of lst, the second element, and the second tail of lst.

Construction of the list structure which we here call x (cons e f) Selection: (car x) => e (cdr x) => f The constructor function cons takes an element e and a list f and constructs a new list. As illustrated above cons makes exactly one new cons cell, and no kind of list copying is involved at all. The selector car returns the first element of the list. A better name of car would be head . The selector cdr returns the list consisting of all but the first element in the list. A better name of cdr would be tail .

A proper list is always terminated by the empty list In Scheme the empty list is denoted '(). When we in this context talk about the termination of the list we mean the value we get by following the cdr references to the end of the list structure.

References R5RS: List and pair functions in Scheme Foldoc: list Foldoc: cons

Symbolic expressions and improper lists Slide Annotated slide Contents Index References Textbook

The cons function is suitable for definition of binary trees with 'data' in the leaves

Figure. A symbolic expression which illustrates the most general form it can take - a binary tree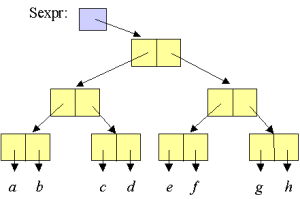

Figure. The same symbolic expression laid out as a list. The expressions is a proper list if and only if h is the empty list. If h is not the empty list, the symbolic expression is an improper list.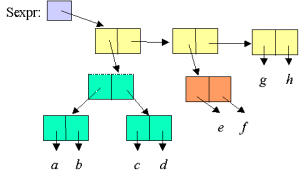

Exercise 2.3. Construction of symbolic expressions

Construct the symbolic expressions illustrated on this page via the cons primitive in Scheme. The entities named a through h should be symbols. As a help, the rightmost part of the structure is made by (cons 'g 'h). 'g is equivalent to (quote g), meaning that g is not evaluated, but taken for face value. Experiment with h being the empty list. Try to use a proper list function, such as length, on your structures.

Practical list construction Slide Annotated slide Contents Index References Textbook

cons is the basic list constructor function - but it can be applied through a number of other means as well

List and S-expression construction: Deep cons expressions Using the list function Using quote or quasiquote also known as backquote

Table. Examples of list construction by use of cons , list and quoted list expressions.

Expression Value (cons 1 (cons 2 (cons (+ 1 2) '()))) (1 2 3) (list 1 2 (+ 1 2)) (1 2 3) (quote (1 2 (+ 1 2))) (1 2 (+ 1 2)) '(1 2 (+ 1 2)) (1 2 (+ 1 2)) (quasiquote (1 2 (unquote (+ 1 2)))) (1 2 3) `(1 2 ,(+ 1 2)) (1 2 3)

Exercise 2.4. Every second element of a list

Write a function, every-second-element, that returns every second element of a list. As examples (every-second-element '(a b c)) => (a c) (every-second-element '(a b c d)) => (a c) It is recommended that you formulate a recursive solution. Be sure to consider the basis case(s) carefully. It is often worthwhile to go for a more general solution than actually needed. Sometimes, in fact, the general solution is simpler than one of the more specialized solutions. Discuss possible generalizations of every-second-element, and implement the one you find most appropriate.

Reference R5RS: Quasiquotation

List functions Slide Annotated slide Contents Index References Textbook

There exists a number of important List functions in Scheme, and we often write other such functions ourselves We will here take a look at some of the most important list functions, as defined by the language itself. You are encouraged to read about them in the Scheme Report, to which we make a reference below.

(null? lst)     A predicate that returns whether lst is empty (list? lst)     A predicate that returns whether lst is a proper list (length lst)     Returns the number of elements in the proper list lst (append lst1 lst2)     Concatenates the elements of two or more lists (reverse lst)     Returns the elements in lst in reverse order (list-ref lst k)     Accesses element number k of the list lst (list-tail lst k)     Returns the k'th tail of the list lst It should be noticed that the first element is designated as element number 0. Thus (list-ref '(a b c) 1) returns b

References R5RS: Pairs and Lists List functions in the general LAML library

Association lists Slide Annotated slide Contents Index References Textbook

An association list is a list of cons pairs Association lists are used in the same way as associative arrays

Table. Examples of association lists. The function assq uses eq? to compare the first parameter with the first element - the key element - in the pairs. As an alternative, we could use the function assoc, which uses equal? for comparison. A better and more general solution would be to pass the comparison function as parameter. Notice in this context, that both assq and assoc are 'traditional Lisp functions' and part of Scheme, as defined in the language report.

Expression Value (define computer-prefs '((peter . windows) (lars . mac) (paw . linux) (kurt . unix))) (assq 'lars computer-prefs) (lars . mac) (assq 'kurt computer-prefs) (kurt . unix) (define computer-prefs-1 (cons (cons 'lene 'windows) computer-prefs)) computer-prefs-1 ((lene . windows) (peter . windows) (lars . mac) (paw . linux) (kurt . unix))

Exercise 2.6. Creation of association lists

Program a function pair-up that constructs an association list from a list of keys and a list of values. As an example (pair-up '(a b c) (list 1 2 3)) should return ((a . 1) (b . 2) (c . 3)) Think of a reasonable solution in case the length of the key list is different from the length of the value list.

Exercise 2.6. Association list and property lists

Association lists have been introduced at this page. An association list is a list of keyword-value pairs (a list of cons cells). Property lists are closely related to association lists. A property list is a 'flat list' of even length with alternating keys and values. The property list corresponding to the following association list ((a . 1) (b . 2) (c . 3)) is (a 1 b 2 c 3) Program a function that converts an association list to a property list. Next, program the function that converts a property list to an association list.

Reference Associative arrays - OOP (in Danish)

Property lists Slide Annotated slide Contents Index References Textbook

A property list is a flat, even length list of associations The HTML/XML/CSS attributes are represented as property lists in LAML documents

Table. A comparison between association lists and property lists. In this example we associate keys (represented as symbols) to string values.

Association list Property list ((peter . "windows") (lars . "mac") (paw . "linux") (kurt . "unix")) (peter "windows" lars "mac" paw "linux" kurt "unix")

Program: A simple LAML document with emphasis on the attributes, represented as property lists. There are four attribute lists (property lists, each with its own color). Notice the CSS attribute css:text-decoration, given inline in the document .

(load (string-append laml-dir "laml.scm")) (laml-style "simple-xhtml1.0-transitional-validating") (write-html 'raw (html 'xmlns "http://www.w3.org/1999/xhtml" (head (meta 'http-equiv "Content-Type" 'content "text/html; charset=iso-8859-1") (title "Attribute Demo")) (body 'id "KN" 'class "generic" (p "Here comes a camouflaged link:") (p (a 'href "http://www.cs.auc.dk" 'css:text-decoration "none" 'target "main" "Link to the CS Department")) (p "End of document.")))) (end-laml)

In the LAML general library there are functions ( alist-to-propertylist and propertylist-to-alist ) that convert between association lists and property lists

References The HTML document that illustrates the property list representation of attributes Manual entry of propertylist-to-alist Manual entry of alist-to-propertylist CSS attributes in HTML mirrors

Tables as lists of rows Slide Annotated slide Contents Index References Textbook

It is natural to represent tables as lists of rows, and to represent a row as a list Tables play an important roles in many web documents LAML has a strong support of tables

Table. Examples of table transposing, row elimination, and column elimination. We will program and illustrate these functions in a later exercise of this material. The function show-table is similar to table-0 from a LAML convenience library. Using higher-order functions it is rather easy to program the show-table function. We will come back to this later in these notes.

Expression Value tab1 (("This" "is" "first" "row") ("This" "is" "second" "row") ("This" "is" "third" "row") ("This" "is" "fourth" "row") ) (show-table tab1) This is first row This is second row This is third row This is fourth row (show-table (transpose-1 tab1)) This This This This is is is is first second third fourth row row row row (show-table (eliminate-row 2 tab1)) This is first row This is third row This is fourth row (show-table (eliminate-column 4 tab1)) This is first This is second This is third This is fourth

Later in this material we will study possible implementations of the function show-table

References Table functions in the HTML4.0 convenience library Future exercise about transposing, row elimination and column elimination Another simple HTML table function

Programs represented as lists Slide Annotated slide Contents Index References Textbook

It is a unique property of Lisp that programs are represented as data, using the main data structure of the language: the list

A sample Scheme program from the LAML library:

Program: The function from the general library that converts different kinds of data to a number.

(define (as-number x) (cond ((string? x) (string->number x)) ((number? x) x) ((char? x) (char->integer x)) ((boolean? x) (if x 1 0)) ; false -> 0, true -> 1 (else (error (string-append "Cannot convert to number " (as-string x))))

In Scheme it is not intended that the program source should be introspected by the running program But in other Lisp systems there is easy access to self reflection

Reference R5RS: Vectors

Besides numbers, Scheme also supports booleans, characters, and symbols

Booleans True is denoted by #t and false by #f Every non-false values count as true in if and cond Characters Characters are denoted as #\a, #\b, ... Some characters have symbolic names, such as #\space, #\newline Symbols Symbols are denoted by quoting their names: 'a , 'symbol , ... Two symbols are identical in the sense of eqv? if and only if their names are spelled the same way

References R5RS: Booleans R5RS: Characters R5RS: Symbols R5RS: Equivalence predicates

Vectors Slide Annotated slide Contents Index References Textbook

Vectors in Scheme are heterogeneous array-like data structures of a fixed size

Vectors are denoted in a similar way as list Example: #(0 a (1 2 3)) Vectors must be quoted in the same way as list when their external representations are used directly The function vector is similar to the function list There are functions that convert a vector to a list and vice versa vector->list list->vector

The main difference between lists and vectors is the mode of access and the mode of construction There is direct access to the elements of a vector. List elements are accessed by traversing a chain of references. This reflects the basic differences between arrays and linked lists. The mode of construction for list is recursive, using the cons function. Lists are created incrementally: New elements can be created when needed, and prepended to the list. Vectors are allocated in one chunck, and cannot be enlarged or decreased incrementally.

References R5RS: Vectors Future exercise about binary search in vectors

Strings Slide Annotated slide Contents Index References Textbook

String is an array-like data structure of fixed size with elements of type character.

The string and vector types have many similar functions A number of functions allow lexicographic comparisons of strings: string=?, string<?, string<=?, ... There are case-independent, ci, versions of the comparison functions. The substring function extracts a substring of a string

Like lists, strings are important for many practical purposes, and it is therefore important to familiarize yourself with the string functions in Scheme

References R5RS: Strings LAML String predicates Other LAML String functions

The concept definition: A definition binds a name to a value

Syntax: A name is first introduced and the name is bound to the value of the expression

(define name expression)

About Scheme define forms Appears normally at top level in a program Creates a new location named name and binds the value of expression to that location In case the location already exists we have a redefinition, and the define form is equivalent to the assignment (set! name expr) Does not allow for imperative programming, because define cannot appear in selections, iterations, etc. Can also appear at certain positions in bodies, but only as syntactic sugar for local binding forms (letrec)

Reference R5RS: Definitions

The conceptual starting point is the well-known mathematical concept of functions The notational starting point is lambda calculus

The mathematical function concept A mapping from a domain to a range A function transfers values from the domain to values in the range A value in the domain has at most a single corresponding value in the range Totally or partially defined functions Extensionally or intensionally defined functions Lambda calculus A very terse notation of functions and function application An extensionally defined function is defined by a set of pairs, enumerating corresponding elements in the domain and range. Notice that this causes practical problems if there are many different values in the domain of the function. An intensionally defined function is based on an algorithm that describes how to bring a value from the domain to the similar value in the range. This is a much more effective technique to definition of most the functions, we program in the functional paradigm.

Reference Foldoc: function

Lambda calculus Slide Annotated slide Contents Index References Textbook

We will here introduce the notation of the lambda calculus, mainly in order to understand the inspiration which led to the concept of lambda expressions in Lisp and Scheme.

Lambda calculus is a more dense notation than the similar Scheme notation

Table. A comparison of the notations of abstraction and combination (application) in the lambda calculus and Lisp. In some variants of lambda calculus there are more parentheses than shown here: (λ v . E). However, mathematicians tend to like ultra brief notation, and they often eliminate the parentheses. This stands as a contrast to Lisp and Scheme programmers.

Lambda calculus Scheme Abstraction λ v . E (lambda (v) E) Combination E1 E2 (E1 E2)

Reference Foldoc: lambda calculus

Functions in Scheme Slide Annotated slide Contents Index References Textbook

Functions are represented as lambda expressions in a source program At run time, functions are represented as first class function objects

Program: A sample read-eval-print session with lambda expressions and function objects. In a context where we define x to the number 6 we first evaluate a lambda expression. Scheme acknowledges this by returning the function object, which prints like ' #<procedure> '. As a contrast to numbers, lists, and other simple values, there is no good surface representation of function values (function objects). Next we bind the name inc to the same function object. More about name binding in a later part of this material. The expression (if (even? x) inc fac) returns inc because the value of x is 6, and as such it is even. Therefore the value of ((if (even? x) inc fac) 5) is the same as the value of (inc 5), namely 6.

> (define x 6) > (lambda (x) (+ x 1)) #<procedure> > (define inc (lambda (x) (+ x 1))) > inc #<procedure:inc> > (if (even? x) inc fac) #<procedure:inc> > ((if (even? x) inc fac) 5) 6

Reference R5RS: Procedures (Functions)

Function objects Slide Annotated slide Contents Index References Textbook

The concept function object: A function object represents a function at run time. A function object is created as the value of a lambda expression		A function object is a first class value at run time, in the same way as numbers, lists and other data are values. This is different from more traditional programming languages, where procedural and functional abstractions have another status than ordinary data.
The concept closure: A function object is also known as a closure.		The name 'closure' is related to the interpretation of free names in the body expression of the function. Free names are used, but not defined in the body. In a function object (or closure) the free names are bound in the context of the lambda expression. This is a contrast to the case where the free names are bound in the context of the application of the function.

Characteristics of function objects: First class objects Does not necessarily have a name A function object can be bound to a name in a definition Functions as closures: Capturing of free names in the context of the lambda expression Static binding of free names A closure is represented as a pair of function syntax and values of free names A function object can be applied on actual parameters, passed as a parameter to a function, returned as the result from another function, and organized as a constituent of a data structure

Functions as first class values Slide Annotated slide Contents Index References Textbook

A function object is a first class citizen

The concept first class citizen: A first class citizen is an entity which can be passed as parameter to functions, returned as a result from a function, and organized as parts of data structures

Program: A few interactions which illustrate the first class properties of function objects. We bind the variable toplevel-html-elements to the list of the two functions html and frameset. Both are HTML mirror functions defined in the LAML general library. We illustrate next that the value of the variable indeed is a list of two functions. Thus, we have seen that we can organized functions as elements in lists. The function cadr returns the second element of a list. It is equivalent to (compose car cdr), where compose is functional composition. In the third evaluation we apply the mirror function frameset on a single frame. The last interaction shows the HTML rendering of the this. xml-render is a function defined in the LAML general library.

1> (define toplevel-html-elements (list html frameset)) 2> overall-html-elements (#<procedure> #<procedure>) 3> ((cadr toplevel-html-elements) (frame 'src "sss")) (ast "frameset" ((ast "frame" () (src "sss") single)) () double) 4> (xml-render ((cadr toplevel-html-elements) (frame 'src "sss"))) "<frameset><frame src = \"sss\"></frameset>"

Reference Foldoc: first class

Anonymous functions Slide Annotated slide Contents Index References Textbook

A function object does not have a name, and a function object is not necessarily bound to a name

Program: An illustration of anonymous functions. The function (lambda(x) (+ x 1)) is the function that adds one (to its parameter). It is organized in a list side by side with the function that multiplies by five. Notice in this context that none of these two functions are named. In the last interaction we apply the latter to the number 6.

1> ((lambda(x) (+ x 1)) 3) 4 2> (define fu-lst (list (lambda (x) (+ x 1)) (lambda (x) (* x 5)))) 3> fu-lst (#<procedure> #<procedure>) 4> ((second fu-lst) 6) 30

Lambda expressions in Scheme Slide Annotated slide Contents Index References Textbook

Syntax:

(lambda (formal-parameter-list) expression)

Syntax:

(lambda formal-parameters-name expression)

Lambda expression characteristics in Scheme: No type declaration of formal parameter names Call by value parameters In reality passing of references to lists and other structures Positional and required parameters (lambda (x y z) expr) accepts exactly three parameters Required and rest parameters (lambda (x y z . r) expr) accepts three or more parameters Rest parameters only (lambda r expr) accepts an arbitrary number of parameters

Exercise 2.7. Parameter passing in Scheme

Familiarize yourself with the parameter passing rules of Scheme by trying out the following calls: ((lambda (x y z) (list x y z)) 1 2 3) ((lambda (x y z) (list x y z)) 1 2) ((lambda (x y z) (list x y z)) 1 2 3 4) ((lambda (x y z . r) (list x y z r)) 1 2 3) ((lambda (x y z . r) (list x y z r)) 1 2) ((lambda (x y z . r) (list x y z r)) 1 2 3 4) ((lambda r r) 1 2 3) ((lambda r r) 1 2) ((lambda r r) 1 2 3 4) Be sure that you can explain all the results

Optional parameters of Scheme functions (1) Slide Annotated slide Contents Index References Textbook

It is often useful to pass one or more optional parameters to a function In case an optional parameter is not passed explicitly, a default value should apply

Program: A example of a function f that accepts optional-parameters. Besides the required parameter rp, the function accepts an arbitrary number of additional parameters, the list of which are bound to the formal parameter optional-parameter-list. The function optional-parameter from the LAML general library accesses information from optional-parameter-list. In case an optional parameter is not passed, the default value (the last parameter of optional-parameter) applies.

(define (f rp . optional-parameter-list) (let ((op1 (optional-parameter 1 optional-parameter-list 1)) (op2 (optional-parameter 2 optional-parameter-list "a")) (op3 (optional-parameter 3 optional-parameter-list #f))) (list rp op1 op2 op3)))

Program: A number of calls of the function f. For clarity we define f as the first interaction.

0> (define (f rp . optional-parameter-list) (let ((op1 (optional-parameter 1 optional-parameter-list 1)) (op2 (optional-parameter 2 optional-parameter-list "a")) (op3 (optional-parameter 3 optional-parameter-list #f))) (list rp op1 op2 op3))) 1> (f 7) (7 1 "a" #f) 2> (f 7 "c") (7 "c" "a" #f) 3> (f 7 8) (7 8 "a" #f) 4> (f 7 8 9) (7 8 9 #f) 5> (f 7 8 9 10) (f 7 8 9 10) 6> (f 7 8 9 10 11) (7 8 9 10)

References Manual entry of optional-parameter HTML mirror functions in LAML

Optional parameters of Scheme functions (2) Slide Annotated slide Contents Index References Textbook

Observations about optional parameters: The function optional-parameter is a LAML function from the general library The optional parameter idea works well if there is a natural ordering of the relevance of the parameters If parameter n is passed, it is also natural to pass parameter 1 to n-1 The idea does not work well if we need to pass optional parameter number n, but not number 1 .. n-1

Keyword parameters is a good alternative to optional parameter lists in case many, 'unordered' parameters need to passed to a function We have demonstrated how we simulate optional parameter via the 'rest parameter list' mechanism in Scheme. It is also possible to simulate a keyword parameter mechanism. In a LAML context, this is done with respect to the passing of attributes to the HTML mirror functions.

Closures Slide Annotated slide Contents Index References Textbook

Functions capture the free names in the context of the lambda expression

An illustration of a closure, as formed by the syntactical lambda expression together with the necessary free names

Reference Function objects

Function definition in Scheme Slide Annotated slide Contents Index References Textbook

A function object can be bound to a name via define like any other kind of value. But we often use a slightly different, equivalent syntax for function definitions, where the 'lambda' is implicitly specified

Syntax: The ordinary way to bind f to the value of a lambda expressions

(define f (lambda (p1 p2) ...))

Syntax: An equivalent syntactic sugaring with a more shallow parenthesis structure. Whenever Scheme identifies a list at the 'name place' in a define form, it carries out the transformation (define (f p1 p2) ...) => (define f (lambda (p1 p2) ...)) . Some Scheme programmers like the form (define (f p1 p2) ...) because the calling form (f p1 p2) is a constituent of the form (define (f p1 p2) ...)

(define (f p1 p2) ...)

Simple web-related functions (1) Slide Annotated slide Contents Index References Textbook

We will here give a simple example of a web-related function. Much more interesting examples will appear later in the material.

Program: The definition of a www-document function. The www-document function is useful if you want to abstract the HTML envelope formed by the elements html, head, title, and body. If you need to pass attributes to html or body the proposed function is not adequate.

(define (www-document the-title . body-forms) (html (head (title the-title)) (body body-forms)))

Program: A sample application of the function www-document. Notice the way we pass a number of body contributions, which - as a list - are bound to the formal parameter body-forms.

(www-document "This is the document title" (h1 "Document title") (p "Here is the first paragraph of the document") (p "The second paragraph has an" (em "emphasized item") "and a" (em "bold face item")_"."))

Program: The whole story - including the LAML context.

(load (string-append laml-dir "laml.scm")) (laml-style "simple-xhtml1.0-transitional-validating") (define (www-document the-title . body-forms) (html (head (title the-title)) (body body-forms))) (www-document "This is the document title" (h1 "Document title") (p "Here is the first paragraph of the document") (p "The second paragraph has an" (em "emphasized item") "and a" (em "bold face item")_"."))

Simple web-related functions (2) Slide Annotated slide Contents Index References Textbook

We will here show another simple function.

Program: The definition of the indent-pixel function. This is a function which we use in many web documents to indent the contents a number of pixels relative to its context. Here we implement the indentation by use of a table, in which the first column cell is empty. As we will se, other possibilities exist.

(define (indent-pixels p . contents) (table 'border "0" (tbody (tr (td 'width (as-string p) "") (td 'width "*" contents)))))

Program: An alternative version of theindent-pixel function. This version uses Cascading Style Sheets expressiveness. As it appears, this is a more compact, and more direct way of achieving our indentation goal.

Program: A sample application of indent-pixel with some initial LAML context (software loading). Notice the use of the XHTML mirror.

References The first version of the indent-pixels document The second version of the indent-pixels document

Function exercises Slide Annotated slide Contents Index References Textbook

Exercise 2.9. Colors in HTML

In HTML we define colors as text strings of length 7:     "#rstuvw" The symbols r, s, t, u, v, and w are all hexadecimal numbers between 0 and f (15). rs is in that way the hexadecimal representation for red, tu is the code for green, and vw is the code for blue. As an example, the text string     "#ffffff" represents white and     "#ff0000" is red. In Scheme we wish to represent a color as the list     (color r g b) where color is a symbol, r is number between 0 and 255 which represents the amount of red, and g and b in a similar way the amount of green and blue in the color. Write a Scheme function that transforms a Scheme color to a HTML color string. It is a good training to program the function that converts decimal numbers to hexa decimal numbers. I suggest that you do that - I did it in fact in my solution! If you want to make life a little easier, the Scheme function (number->string n radix) is helpful (pass radix 16 as second parameter).

Exercise 2.9. Letter case conversion

In many web documents it is desirable to control the letter case of selected words. This allows us to present documents with consistent appearances. Therefore it is helpful to be able to capitalize a string, to transform a string to consist of upper case letters only, and to lower case letters only. Be sure to leave non-alphabetic characters untouched. Also, be sure to handle the Danish characters 'æ', 'ø', and 'å' (ASCII 230, 248, and 229 respectively). In addition, let us emphasize that we want functions that do not mutate the input string by any means. (It means that you are not allowed to modify the strings passed as input to your functions). Write functions capitalize-a-string, upcase-a-string, downcase-a-string for these purposes. As examples of their use, please study the following:     (capitalize-a-string "monkey") => "Monkey"     (upcase-a-string "monkey") => "MONKEY"     (downcase-a-string "MONkey") => "monkey" Hint: I suggest that you program the necessary functions yourself. Convert the string to a list of ASCII codes, do the necessary transformations on this list, and convert the list of modified ASCII codes back to a string. The Scheme functions list->string and string->list are useful. Hint: If you want to make life a little easier (and learn less from this exercise...) you can use the Scheme functions char-upcase and char-downcase, which work on characters. But these functions do maybe not work on the Danish letters, so you you probably need some patches.

Chapter 2: Expressions, Types, and Functions
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: July 2, 2013, 09:14:42