Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark

Abstract Previous lecture Next lecture Index References Contents

In this lecture we will study the impact of the order of evaluation.

Two equal expressions can substitute each other without affecting the meaning of a functional program

Referential transparency provides for easy equational reasoning about a program does not rely on a particular notion of equality Reference equality, shallow equality and deep equality cannot be distinguished by functional means is a major contrast to imperative programming

Equals can be replaced by equals

References Foldoc: referential transparency Equality in Scheme

An illustration of referential transparency Slide Annotated slide Contents Index References Textbook

With referential transparency it is possible to perform natural program transformations without any concern of side effects

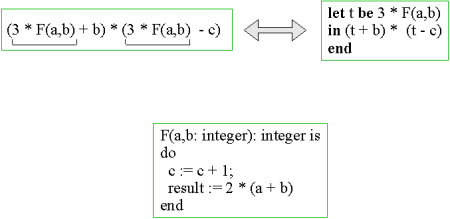
Figure. It is possible to rewrite one of the expressions above to the other, provided that F is a function. Below, we have illustrated an example where F is of procedural nature. Notice that F assigns the variable c, such that it becomes critical to know how many times F is called.

In a functional program an expression is evaluated with the purpose of producing a value An expression is composed of subexpressions

Figure. An illustration of an expression with subexpressions.

Subexpressions can be evaluated in an arbitrary order provided that no errors occur in subexpressions the evaluation of all subexpressions terminates It is possible, and without problems, to evaluate subexpressions in parallel

A motivating example Slide Annotated slide Contents Index References Textbook

What is the value of the following expression?

Program: A constant function with an actual parameter expression, the evaluation of which never terminates.

((lambda (x) 1) some-infinite-calculation)

Program: A more concrete version of the expression from above. The function infinite-calculation just calls itself without ever terminating.

(define (infinite-calculation) (infinite-calculation)) ((lambda (x) 1) (infinite-calculation))

A motivating example - clarification Slide Annotated slide Contents Index References Textbook

What is the value of the following expression?

Program: A constant function with an actual parameter expression, the evaluation of which never terminates.

((lambda (x) 1) some-infinite-calculation)

Program: A variation of the example in Scheme.

(define (infinite-calculation) (infinite-calculation)) ((lambda (x) 1) (infinite-calculation))

Different evaluation orders give different 'results' The number 1 A non-terminating calculation Two different semantics of function application are involved: Strict: A function call is well-defined if and only if all actual parameters are well-defined Non-strict: A function call can be well-defined even if one or more actual parameters cause an error or an infinite calculation

The rewrite rules define semantics preserving transformations of expressions The goal of applying the rewrite rules is normally to reduce an expression to the simplest possible form, called a normal form.

Overview of rewrite rules Alpha conversion: rewrites a lambda expression Beta conversion: rewrites general function calls Expresses the idea of substitution, as described by the substitution model Eta conversion: rewrites certain lambda expressions to a simpler form

The alpha rewrite rule Slide Annotated slide Contents Index References Textbook

An alpha conversion changes the names of lambda expression formal parameters

The concept alpha conversion: Formal parameters of a lambda expression can be substituted by other names, which are not used as free names in the body

Legal conversion:

Table. An example of an alpha rewriting. The name a replaces x and the name b replaces y.

Expression Converted Expression (lambda (x y) (f x y)) (lambda (a b) (f a b))

Illegal conversion:

Table. Examples of an illegal alpha conversion. f is a free name in the lambda expression. A free name is used, but not defined (bound) in the lambda expression. In case we rename one of the parameters to f, the free name will be bound, hereby causing an erroneous name binding.

Expression Converted Expression (lambda (x y) (f x y)) (lambda (a f) (f a f))

Reference Foldoc: alpha conversion

The beta rewrite rule Slide Annotated slide Contents Index References Textbook

A beta conversion tells how to evaluate a function call

The concept beta conversion: An application of a function can be substituted by the function body, in which formal parameters are substituted by the corresponding actual parameters

Legal conversions:

Table. Examples of beta conversions. In all the three examples the function calls are replaced by the bodies. In the bodies, the formal parameters are replaced by actual parameters.

Expression Converted Expression ((lambda(x) (f x)) a) (f a) ((lambda(x y) (* x (+ x y))) (+ 3 4) 5) (* 7 (+ 7 5)) ((lambda(x y) (* x (+ x y))) (+ 3 4) 5) (* (+ 3 4) (+ (+ 3 4) 5))

Reference Foldoc: beta conversion

The eta rewrite rule Slide Annotated slide Contents Index References Textbook

An eta conversion lifts certain function calls out of a lambda convolute

The concept eta conversion: A function f, which only passes its parameters on to another function e, can be substituted by e

(lambda(x) (e x)) <=> e   provided that x is not free in the expression e

Legal conversion:

Table. An example of an eta rewriting.

Expression Converted Expression (lambda (x) (square x)) square

Illegal conversion:

Table. An example of an illegal eta conversion. The eta conversion rule says in general how 'e' is lifted out of the lambda expressions. In this example, e corresponds to the emphasized inner lambda expression (which is blue on a color medium.) However, x is a free name in the inner lambda expression, and therefore the application of the eta rewrite rule is illegal.

Expression Converted Expression (lambda(x) ((lambda(y) (f x y)) x)) (lambda(y) (f x y))

Reference Foldoc: eta conversion

Normal forms Slide Annotated slide Contents Index References Textbook

Normal forms represent our intuition of the value of an expression

The concept normal form: An expressions is on normal form if it cannot be reduced further by use of beta and eta conversions

About normal forms Alpha conversions can be used infinitely, and as such they do not play any role in the formulation of a normal form A normal form is a particular simple expression, which is equivalent to the original expression, due to the application of the conversions

Is a normal form always unique?

Reference Foldoc: normal form

The ordering of reductions Slide Annotated slide Contents Index References Textbook

Given a complex expression, there are many different orderings of the applicable reductions

The concept normal-order reduction: Using normal-order reduction, the first reduction to perform is the one at the outer level of the expression
The concept applicative-order reduction: Using applicative-order reduction, the first reduction to perform is the inner leftmost reduction

Normal-order reduction represents evaluation by need Applicative-order reduction evaluates all constituent expressions, some of which are unnecessary or perhaps even harmful. As such, there is often a need to control the evaluation process withspecial formsthat use a non-standard evaluation strategy

An example of normal versus applicative evaluation Slide Annotated slide Contents Index References Textbook

Reduction of the expression ((lambda(x y) (+ (* x x) (* y y))) (fak 5) (fib 10))

Figure. Normal vs. applicative reduction of a Scheme expression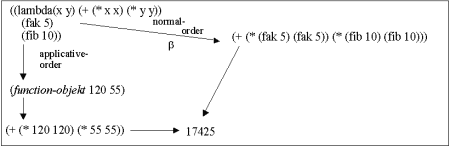

Program: The necessary Scheme stuff to evaluate the expression.

(define (fak n) (if (= n 0) 1 (* n (fak (- n 1))))) (define (fib n) (cond ((= n 0) 0) ((= n 1) 1) (else (+ (fib (- n 1)) (fib (- n 2)))))) ((lambda(x y) (+ (* x x) (* y y))) (fak 5) (fib 10))

It appears to be the case that normal order reduction can lead to repeated evaluation of the same subexpression

Theoretical results Slide Annotated slide Contents Index References Textbook

The theoretical results mentioned on this page assure some very satisfactory properties of functional programming

Figure. The rewriting => is confluent if for all e, e1 and e2, for which e => e1 and e => e2, there exists an e3 such that e1 => e3 and e2 => e3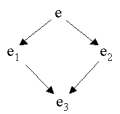

The first Church-Rosser theorem. Rewriting with beta and eta conversions are confluent.

The second Church-Rosser theorem. If e0 => ... => e1, and if e1 is on normal form, then there exists a normal order reduction of e0 to e1

Reference Foldoc: church-rosser

Practical implications Slide Annotated slide Contents Index References Textbook

We will here describe the practical consequences of the theoretical results mentioned on the previous page

During the evaluation of an expression, it will never be necessary to backtrack the evaluation process in order to reach a normal form. An expression cannot be converted to two different normal forms (modulo alpha conversions, of course). If an expression e somehow can be reduced to f in one or more steps, f can be reached by normal order reduction - but not necessarily by applicative order reduction

Normal-order reduction is more powerful than the applicative-order reduction Scheme and ML uses applicative-order reduction Haskell is an example of a functional programming language with normal-order reduction

Conditionals and sequential boolean operators Slide Annotated slide Contents Index References Textbook

There are functional language constructs - special forms - for which applicative order reduction would not make sense

(if b x y) Depending on the value of b, either x or y are evaluated It would often be harmful to evaluate both x and y before the selection (define (fak n) (if (= n 0) 1 (* n (fak (- n 1)))))

(and x y z) and evaluates its parameter from left to right In case x is false, there is no need to evaluate y and z Often, it would be harmful to evaluate y and z (and (not (= y 0)) (even? (quotient x y)))

Lazy evaluation Slide Annotated slide Contents Index References Textbook

We will now deal with a practical variant of normal-order reduction

The concept lazy evaluation: Lazy evaluation is an implementation of normal-order reduction which avoids repeated calculation of subexpressions

Figure. An illustration of lazy evaluation of a Scheme expression. Notice, that Scheme does not evaluate the expression in this way. Scheme uses applicative-order reduction.

Reference Foldoc: lazy evaluation

Scheme does not support normal-order reduction nor lazy evaluation Scheme has an explicit primitive which delays an evaluation

Syntax:

(delay expr) => promise

Syntax:

(force promise) => value

Program: A principled implementation of delay and force in Scheme.

Program: Real implementations of delay. The first definition uses the R5RS macro facility, whereas the last one uses a more primitive macro facility, which happens to be supported in MzScheme.

References R5RS: delay R5RS: force

Examples of delayed evaluation Slide Annotated slide Contents Index References Textbook

Table. Examples of use of delay and force.

Expression Value (delay (+ 5 6)) #<promise> (force 11) error (let ((delayed (delay (+ 5 6)))) (force delayed)) 11

Infinite lists in Scheme: Streams Slide Annotated slide Contents Index References Textbook

We can work with lists of infinite length by delaying the evaluation of every list tail using delay As an invariant, every list tail will be delayed

Program: Stream primitives. Notice the way head is defined to be an alias of car.

Program: An implementation of cons-stream in R5RS Scheme.

The functions mentioned above stem from the book Structure and Interpretation of Computer Programs

Reference SICP: Streams

Example streams Slide Annotated slide Contents Index References Textbook

Table. Examples of streams. ones is an infinite streams of the element 1. stream-section is a function that returns a finite section of a potentially infinite stream. nat-nums is stream of all the natural numbers, made by use of the recursive function integers-starting-from. The fourth row shows an alternative definition of nat-nums. Finally, fibs is the infinite stream of Fibonacci numbers.

Expression Value (define ones (cons-stream 1 ones)) (1 . #<promise>) (stream-section 7 ones) (1 1 1 1 1 1 1) (define (integers-starting-from n) (cons-stream n (integers-starting-from (+ n 1)))) (define nat-nums (integers-starting-from 1)) (stream-section 10 nat-nums) (1 2 3 4 5 6 7 8 9 10) (define nat-nums (cons-stream 1 (add-streams ones nat-nums))) (stream-section 10 nat-nums) (1 2 3 4 5 6 7 8 9 10) (define fibs (cons-stream 0 (cons-stream 1 (add-streams (tail fibs) fibs)))) (stream-section 15 fibs) (0 1 1 2 3 5 8 13 21 34 55 89 144 233 377)

Program: The functions stream-section and add-streams.

Program: All Scheme stream stuff collected in one file.

Stream example: The sieve of Eratosthenes Slide Annotated slide Contents Index References Textbook

The Sieve of Eratosthenes is a more sophisticated example of the use of streams

Program: The sieve stream function.

(define (sieve stream) (cons-stream (head stream) (sieve (filter-stream (lambda (x) (not (divisible? x (head stream)))) (tail stream)))))

Figure. An illustration of the generation of prime numbers in The Sieve of Eratosthenes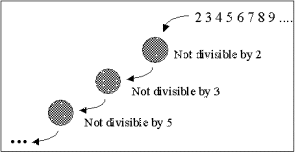

Applications of The sieve of Eratosthenes Slide Annotated slide Contents Index References Textbook

The sieve process produces the stream of all prime numbers

Table. The first 25 prime numbers made by sieving a sufficiently long prefix of the integers starting from 2.

Expression Value (define primes (sieve (integers-starting-from 2))) (stream-section 25 primes) (2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97)

Program: All the functions necessary to use the Sieve of Eratosthenes. In addition, however, you must load the Scheme stream stuff. The most remarkable function is filter-streams, which illustrates that it is necessary to rewrite all our classical higher order function to stream variants. This is clearly a drawback!

(define (sieve stream) (cons-stream (head stream) (sieve (filter-stream (lambda (x) (not (divisible? x (head stream)))) (tail stream))))) (define (divisible? x y) (= (remainder x y) 0)) (define (filter-stream p lst) (cond ((empty-stream? lst) the-empty-stream) ((p (head lst)) (cons-stream (head lst) (filter-stream p (tail lst)))) (else (filter-stream p (tail lst))))) (define (integers-starting-from n) (cons-stream n (integers-starting-from (+ n 1)))) (define primes (sieve (integers-starting-from 2)))

Chapter 5: The Order of Evaluation
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: January 3, 2014, 09:34:07