Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark

Abstract Previous lecture Next lecture Index References Contents

In this lecture we continue the introduction to functional programming in Scheme. We start with name binding issues, and proceed with conditional expressions, and recursion and iteration.

The concept name binding expression: A name binding expression establishes a number of local name bindings in order to ease the evaluation of a body expression

In a name binding construct a number of names are bound to values. The name bindings can be used in the body, which must be an expression when we are working in the functional paradigm. There are a number of variations in the way the names can refer to each other mutually. We will meet some of them on the following pages.

Syntax: The names n 1 ... n k are bound to the respective values e 1 ... e k , and the body expression is evaluated relative to these name bindings. Free names in the body expression are bound to names defined in the surround of the let construct.

(let ((n1 e1) ... (nk ek)) body-expr)

Characteristics of a let construct: In body-expr n1 refers to the value of e1, ..., and nk refers to the value of ek Syntactic sugar for an immediate call of a lambda expression To be illustrated on the next page As a consequence, the names are bound simultaneously relative to the name bindings in effect in the context of the let construct.

References R5RS: Binding Constructs (let, let*, letrec) Foldoc: let

The equivalent meaning of let Slide Annotated slide Contents Index References Textbook

We will here understand the underlying, equivalent form of a let name binding construct

Syntax:

(let ((n1 e1) ... (nk ek)) body-expr)

Syntax:

((lambda (n1 ... nk) body-expr) e1 ... ek)

Examples with let name binding Slide Annotated slide Contents Index References Textbook

Table. Examples of namebindings with let. The first example shows that all constituents of a function call can be bound to local names - in the example both the function object referred to by a, and two string parameters. The second example illustrates that alternative names, aliases, can be defined for a couple of functions. Notice in particular that g is bound to b (the bold face function), not em (the emphasis function). This can also be seen in the second column. The third example is a little more advanced, and it can first be understood fully on the ground of the material in the lecture about higher-order functions. We bind the name phrase-elements to a list of ten functions. Via mapping, we apply each function to foo, and we present the results in an ul list.

Expression Value after rendering (let ((anchor "An anchor text") (url "http://www.cs.auc.dk") (tag a) ) (tag 'href url anchor)) An anchor text (let ((f b)) (let ((f em) (g f)) (p (f "Text 1") (g "Text 2")))) Text 1 Text 2 (let ((phrase-elements (list em strong dfn code samp kbd var cite abbr acronym)) ) (ul (map (lambda (f) (li (f "foo"))) phrase-elements))) foo foo foo foo foo foo foo foo foo foo

The let* name binding construct Slide Annotated slide Contents Index References Textbook

It is often useful to be able to use previous name bindings in a let construct, which binds several names

Syntax:

(let* ((n1 e1) ... (ni-1 ei-1) (ni ei) ... (nk ek)) body-expr)

Characteristics of let*: It is possible to refer to n1 through ni-1 from the expression ei Syntactic sugar for k nested let name bindings

An example with let* Slide Annotated slide Contents Index References Textbook

Program: A typical example using sequential name binding. The task is to calculate the number of days, hours, minutes, and seconds given a number of seconds. We subsequently calculate a number of quotients and rest. While doing so we find the desired results. In this example we would not be able to use let; let* is essential because a given calculation depends on previous name bindings. The full example, including the definition of the constants, can be found in the accompanying elucidative program. The function is part of the LAML time library in lib/time.scm of the LAML distribution. The time library is used whenever we need to display time information, such as 'the time of generation' of some HTML files.

(define (how-many-days-hours-minutes-seconds n) (let* ((days (quotient n seconds-in-a-day)) (n-rest-1 (modulo n seconds-in-a-day)) (hours (quotient n-rest-1 seconds-in-an-hour)) (n-rest-2 (modulo n-rest-1 seconds-in-an-hour)) (minutes (quotient n-rest-2 60)) (seconds (modulo n-rest-2 60)) ) (list days hours minutes seconds)))

A set of functions for handling of time. The set of functions elucidated here is only a subset of the LAML time library.

A set of functions for handling of time.

Reference Manual of the LAML time library

The letrec namebinding construct Slide Annotated slide Contents Index References Textbook

The letrec name binding construct allows for definition of mutually recursive functions

Syntax:

(letrec ((n1 e1) ... (nk ek)) body-expr)

Program: An schematic example of a typical application of letrec for local definition of two mutually recursive functions.

(letrec ((f1 (lambda (...) ... (f2 ...))) (f2 (lambda (...) ... (f1 ...))) ) body-expr)

Characteristics of letrec Each of the name bindings have effect in the entire letrec construct, including e1 to ek

LAML time functions Slide Annotated slide Contents Index References Textbook

The function how-many-days-hours-minutes-seconds is part of the LAML time library, which we here illustrate by means of a number of examples.

Table. Example use of some of the LAML time library functions

Expression Value (current-time) 999789132 (time-decode 1000000000) (2001 9 9 3 46 40) (time-decode 0) (1970 1 1 2 0 0) (time-interval 1000000000) (31 8 2 5 1 46 40) (weekday (current-time)) Thursday (danish-week-number (current-time)) 36

if and cond are special forms which evaluate their expressions according to the value of one or more boolean selectors if and cond are not control structures when applied in the functional paradigm Control structures belong to the imperative paradigm. In the functional paradigm, if and cond are used in conditional expressions. By that we mean expressions, of which subexpressions are selected for evaluation based on one or or more boolean selectors.

Syntax:

(if bool-expr expr1 expr2)

Syntax:

(cond (bool-expr1 expr1) ... (bool-exprk exprk) (else exprk+1))

if evaluates expr1 if bool-expr is true, and expr2 if bool-expr is false cond evaluates the first expression expri whose guarding bool-expri is true. If bool-expr1, ..., bool-exprkare all false, the value of cond becomes the value of exprk+1

Exercise 3.2. HTML Header functions

This is a small exercise that aims at construction of slightly different header functions than those provided by the native header functions h1, ..., h6. Define a function (header level) which takes a parameter level. The header function should return the similar basic header function provided that n is between one and six. If n is outside this interval, we want header to return the identity function of one parameter. It means that ((header 3) "Header text") is equal to (h3 "Header text") and that ((h 0) "Header text") is just "Header text". Hint: Arrange the header functions in a list, and let header select the appropriate header function from this list. Define a variant of header which returns a native header function if it receives a single parameter (level), and which returns the value, such as, ((header 3) "Header text"), if it receives both a level parameter and a header text string.

References R5RS: if R5RS: cond

Examples with if Slide Annotated slide Contents Index References Textbook

Table. Examples using an if conditional expression on a Wednesday. In both examples we extract the weekday (a string) from the current time. If it is a Wednesday we emit a paragraph which serves as a reminder of a meeting the following day. If not executed on a Wednesday, we do not want any special text. We achieve this by returning the empty list, which is spliced into the the body context (in the first example) and into the paragraph context (in the second example). The splicing is a result of the handling of lists by the HTML mirror functions in LAML. The two examples differ slightly. In the first example the if is placed on the outer level, feeding information to body. In the second row, the if is placed at an inner level, feeding information to the p function. The two examples also give slightly different results. Can you characterize the results?

Expression Value (body (if (string=? (weekday (current-time)) "Wednesday") (p (em "Remember Thursday meeting!")) '( )) (h1 "Schedule") (p "...")) Remember the Thursday meeting tomorrow! Schedule ... (body (p (if (string=? (weekday (current-time)) "Wednesday") (em "Remember Thursday meeting!") '( ))) (h1 "Schedule") (p "...")) Remember the Thursday meeting tomorrow! Schedule ...

Reference HTML mirror functions and lists

Example with cond: leap-year? Slide Annotated slide Contents Index References Textbook

Program: The function leap-year?. The function returns whether a year y is a leap year. For clarity we have programmed the function with a conditional. In this case, we can express the leap year condition as a simple boolean expression using and and or. We refer to this variation below, and we leave it to you to decide which version you prefer.

(define (leap-year? y) (cond ((= (modulo y 400) 0) #t) ((= (modulo y 100) 0) #f) ((= (modulo y 4) 0) #t) (else #f)))

Program: The function leap year programmed without a conditional. To ease comparison, the original version is shown below the new version.

(define (leap-year? y) (or (= (modulo y 400) 0) (and (= (modulo y 4) 0) (not (= (modulo y 100) 0))))) (define (original-leap-year? y) (cond ((= (modulo y 400) 0) #t) ((= (modulo y 100) 0) #f) ((= (modulo y 4) 0) #t) (else #f)))

A complete program for handling of time

A complete program for handling of time

Example with cond: american-time Slide Annotated slide Contents Index References Textbook

Program: The function american-time. The function returns a string displaying the 'am/pm/noon' time given hour h, minute m, and seconds s.

(define (american-time h m s) (cond ((< h 0) (laml-error "Cannot handle this hour:" h)) ((and (= h 12) (= m 0) (= s 0)) "noon") ((< h 12) (string-append (format-hour-minutes-seconds h m s) " " "am")) ((= h 12) (string-append (format-hour-minutes-seconds h m s) " " "pm")) ((and (= h 24) (= m 0) (= s 0)) "midnight") ((<= h 24) (string-append (format-hour-minutes-seconds (- h 12) m s) " " "pm")) (else (laml-error "Cannot handle this hour:" h))))

Program: The function american-time with helping functions.

(define (american-time h m s) (cond ((< h 0) (laml-error "Cannot handle this hour:" h)) ((and (= h 12) (= m 0) (= s 0)) "noon") ((< h 12) (string-append (format-hour-minutes-seconds h m s) " " "am")) ((= h 12) (string-append (format-hour-minutes-seconds h m s) " " "pm")) ((and (= h 24) (= m 0) (= s 0)) "midnight") ((<= h 24) (string-append (format-hour-minutes-seconds (- h 12) m s) " " "pm")) (else (laml-error "Cannot handle this hour:" h)))) (define (format-hour-minutes-seconds h m s) (string-append (zero-pad-string (number->string h)) ":" (zero-pad-string (number->string m)) ":" (zero-pad-string (number->string s)))) (define (zero-pad-string str) (if (= 1 (string-length str)) (string-append "0" str) str))

Example with cond: as-string Slide Annotated slide Contents Index References Textbook

Program: The function as-string converts a variety of Scheme data types to a string. This function makes use of the fact that any kind of data can be passed to the function, without intervening static type check. At run time we dispatch on the type of x. The function string-merge is discussed later in this section, cf. the reference from this page. The function as-string, and its sibling functions as-number, as-char, as-symbol, and as-list are used heavily in all LAML software. The functions are convenient because they do not need to know the type of the input data. In functional languages with static type checking, we cannot program these functions as shown above. In these language we could overload the function name as-string, and underneath define a number of individual functions each taking a particular type of input.

(define (as-string x) (cond ((number? x) (number->string x)) ((symbol? x) (symbol->string x)) ((string? x) x) ((boolean? x) (if x "true" "false")) ; consider "#t" and "#f" as alternatives ((char? x) (char->string x)) ((list? x) (string-append "(" (string-merge (map as-string x) (make-list (- (length x) 1) " ")) ")")) ((vector? x) (let ((lst (vector->list x))) (string-append "#(" (string-merge (map as-string lst) (make-list (- (length lst) 1) " ")) ")"))) ((pair? x) (string-append "(" (apply string-append (map (lambda (y) (string-append (as-string y) " ")) (proper-part x)) ) " . " (as-string (first-improper-part x)) ")")) (else "??")))

References string-merge example Manual of the LAML general library

Recursive functions are indispensable for the processing of recursive data structures

The concept recursion: Recursion is an algorithmic program solving idea that involves solution of subproblems of the same nature as the overall problem

Given a problem P If P is trivial then solve it immediately If P is non-trivial, divide P into subproblems P1 ,..., Pn Observe if Pi (i=1..n) are of the same nature as P If so, use the overall problem solving idea on each of P1 ... Pn Combine solutions of the subproblems P1 ... Pn to a solution of the overall problem P The problem solving technique sketched here is called divide and conquer. It is not all divide and conquer problems that involve recursion. But many do in fact. Recursion comes into play when the subproblems P1 ... Pn turn out to be of the same nature as the overall problem, and as such they can be solved by the same 'medicine' as used for the overall problem P.

References Foldoc: recursion Recursion - an ECIU material

List processing Slide Annotated slide Contents Index References Textbook

A list is a recursive data structure As a consequence list processing is done via recursive functions We illustrate list processing by extracting attribute values from a LAML attribute property list

Program: A function for extraction of the href attribute from a property list.

; Return the href attribute value from a property list ; Return #f if no href attribute is found. ; Pre-condition: attr-p-list is a property list - ; of even length. (define (find-href-attribute attr-p-list) (if (null? attr-p-list) #f (let ((attr-name (car attr-p-list)) (attr-value (cadr attr-p-list)) (attr-rest (cddr attr-p-list))) (if (eq? attr-name 'href) attr-value (find-href-attribute attr-rest)))))

Program: An example with property lists that represent HTML attributes in LAML. As the last interaction, we see the function find-href-attribute in play.

1> (define a-clause (a 'id "myid" 'class "myclass" 'href "http://www.cs.auc.dk")) 2> a-clause (ast "a" () (id "myid" class "myclass" href "http://www.cs.auc.dk" shape "rect") double xhtml10-strict) 3> (render a-clause) "<a id = \"myid\" class = \"myclass\" href = \"http://www.cs.auc.dk\"></a>" 4> (define attr-list (ast-attributes a-clause)) 5> attr-list (id "myid" class "myclass" href "http://www.cs.auc.dk" shape "rect") 6> (find-href-attribute attr-list) "http://www.cs.auc.dk" >

References AST functions in LAML Property lists Lists in Scheme

Tree processing (1) Slide Annotated slide Contents Index References Textbook

A tree is a recursive data structure We illustrate how to extract information from an HTML syntax tree

Program: A sample web document with a number of links. The link forms - represented by a elements - are highlighted.

(load (string-append laml-dir "laml.scm")) (laml-style "simple-xhtml1.0-strict-validating") (write-html '(prolog pp) (html (head (title "Demo Links")) (body (p "ACM has a useful" (a 'href "http://www.acm.org/dl" "digital library") ) (p "The following places are also of interest:") (ul (li (a 'href "http://www.ieee.org/ieeexplore/" "The IEEE")) (li "The" (a 'href "http://www.w3c.org" "W3C") "site") (li (a 'href "http://link.springer.de/link/service/series/0558/" "Lecture Notes in Computer Science"))) (p "Kurt Nørmark" (br) (a 'href "http://www.cs.auc.dk" "Dept. of Comp. Science") (br) (a 'href "http://www.auc.dk" "Aalborg University"))))) (end-laml)

Program: The abstract syntax tree represented as nested lists. It is hard to read and understand this representation of the tree structure. It is not really oriented towards human reading.

(ast "html" ((ast "head" ((ast "title" ("Demo Links") () double xhtml10-strict)) () double xhtml10-strict) #t (ast "body" ((ast "p" ("ACM has a useful" #t (ast "a" ("digital library") (href "http://www.acm.org/dl" shape "rect") double xhtml10-strict)) () double xhtml10-strict) #t (ast "p" ("The following places are also of interest:") () double xhtml10-strict) #t (ast "ul" ((ast "li" ((ast "a" ("The IEEE") (href "http://www.ieee.org/ieeexplore/" shape "rect") double xhtml10-strict)) () double xhtml10-strict) #t (ast "li" ("The" #t (ast "a" ("W3C") (href "http://www.w3c.org" shape "rect") double xhtml10-strict) #t "for web standards") () double xhtml10-strict) #t (ast "li" ((ast "a" ("Lecture Notes in Computer Science") (href "http://link.springer.de/link/service/series/0558/" shape "rect") double xhtml10-strict)) () double xhtml10-strict)) () double xhtml10-strict) #t (ast "p" ("Kurt Nørmark" #t (ast "br" () () single xhtml10-strict) #t (ast "a" ("Department of Computer Science") (href "http://www.cs.auc.dk" shape "rect") double xhtml10-strict) #t (ast "br" () () single xhtml10-strict) #t (ast "a" ("Aalborg University") (href "http://www.auc.dk" shape "rect") double xhtml10-strict)) () double xhtml10-strict)) () double xhtml10-strict)) (xmlns "http://www.w3.org/1999/xhtml") double xhtml10-strict)

Figure. The syntax tree of the web document with the root made up by the html element.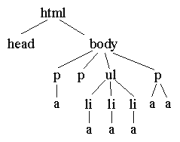

Reference The HTML version of the web document that illustrates tree traversal

Tree processing (2) Slide Annotated slide Contents Index References Textbook

Tree processing is done via recursive functions We illustrate how to extract all URLs from the a elements

Program: The link extraction functions.

; Return a list of URLS as located in the a elements of ast. (define (extract-links ast) (if (ast? ast) (let ((name (ast-element-name ast)) (subtrees (ast-subtrees ast)) ) (if (equal? name "a") (let ((href-attr-value (find-href-attribute (ast-attributes ast)))) (if href-attr-value (list href-attr-value) '())) (extract-links-ast-list subtrees))) '())) ; Return a list of URLS as located in the a elements of ; the list of ast's as passed in ast-list. (define (extract-links-ast-list ast-list) (if (null? ast-list) '() (append (extract-links (car ast-list)) (extract-links-ast-list (cdr ast-list)))))

Program: A link extraction dialogue.

1> (define doc-ast (html (head (title "Demo Links")) (body ...))) 2 > (extract-links doc-ast) ("http://www.acm.org/dl" "http://www.ieee.org/ieeexplore/" "http://www.w3c.org" "http://link.springer.de/link/service/series/0558/" "http://www.cs.auc.dk" "http://www.auc.dk")

Exercise 3.3. The function outline-copy

Program a function outline-copy which makes a deep copy of a list structure. Non-list data in the list should all be translated to a symbol, such as '-. You should be able to handle both proper lists and improper lists. As an example: (outline-copy '((a b c) (d e . f) (h i))) => ((- - -) (- - . -) (- -))

Reference AST functions in LAML

Recursion versus iteration Slide Annotated slide Contents Index References Textbook

Recursive functions are - modulo use of memory resources - sufficient for any iterative need Tail recursive functions in Scheme are memory efficient for programming of any iterative process

The concept tail recursion: Tail recursion is a variant of recursion in which the recursive call takes place without contextual, surrounding calculations in the recursive function.

A tail call is the last 'thing' to be done before the function returns. Therefore there is no need to maintain any activation record of such a call - we can reuse the previous activation record. The image series below will illustrate this.

Image series: A recursive formulation of the function fak and the accompanying recursive process

A recursive formulation of the function fak and the accompanying recursive process

Image no. 1. The recursion is developed - activation records are stacked

 

Image no. 2. The recursion is developed - activation records are stacked

 

Image no. 3. The recursion is developed - activation records are stacked

 

Image no. 4. The recursion is developed - activation records are stacked

 

Image no. 5. The turning point is reached - now on to actual multiplication

 

Image no. 6. Trivial multiplication with 1

 

Image no. 7. Yet another time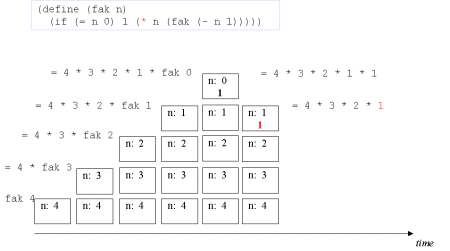

 

Image no. 8. Multiplication with 2

 

Image no. 9. Multiplication with 3

 

Image no. 10. Multiplication with 4

 

Image series: A tail recursive formulation of the function fak and the accompanying iterative process without memory optimization

A tail recursive formulation of the function fak and the accompanying iterative process without memory optimization

Image no. 1. The recursion develops - multiplication with 4

 

Image no. 2. The recursion develops - multiplication with 3

 

Image no. 3. The recursion develops - multiplication with 2

 

Image no. 4. The recursion develops - multiplication with 1

 

Image no. 5. Turning point - we have the result in r

 

Image no. 6. Non-productive unstacking

 

Image no. 7. Non-productive unstacking

 

Image no. 8. Non-productive unstacking

 

Image no. 9. Non-productive unstacking

 

Image no. 10. Non-productive unstacking

 

Image series: A tail recursive formulation of the function fak and the accompanying, memory optimized iterative process

A tail recursive formulation of the function fak and the accompanying, memory optimized iterative process

Image no. 1. Multiplication with 4

 

Image no. 2. Multiplication with 3 - frame reused

 

Image no. 3. Multiplication with 2 - frame reused

 

Image no. 4. Multiplication with 1 - frame reused

 

Image no. 5. Done - the result is in r

 

References R5RS: Proper tail recursion Foldoc: iteration Foldoc: recursion

Example of recursion: number-interval Slide Annotated slide Contents Index References Textbook

The function number-interval returns a list of integers from a lower bound to an upper bound

Program: The function number-interval from the general LAML library. This function returns a list of t-f+1 numbers from f to t .Try it out!.

(define (number-interval f t) (if (<= f t) (cons f (number-interval (+ f 1) t)) '()))

Program: The function number-interval-iter is an iterative, tail recursive variant of number-interval.

(define (number-interval-iter f t) (reverse (number-interval-iter-help f t '()))) (define (number-interval-iter-help f t res) (if (<= f t) (number-interval-iter-help (+ f 1) t (cons f res)) res))

Program: A sample dialogue with the number interval functions.

1> (number-interval 1 10) (1 2 3 4 5 6 7 8 9 10) 2> (number-interval-iter 10 20) (10 11 12 13 14 15 16 17 18 19 20) 3> (number-interval-iter 20 10) ()

Exercise 3.5. The append function

The function append, which is a standard Scheme function, concatenates two or more lists. Let us here show a version which appends two lists: (define (my-append lst1 lst2) (cond ((null? lst1) lst2) (else (cons (car lst1) (my-append (cdr lst1) lst2))))) We will now challenge ourselves by programming an iterative solution, by means of tail recursion. We start with the standard setup: (define (my-next-append lst1 lst2) (my-next-append-1 lst1 lst2 ...)) where my-next-append-1 is going to be the tail recursive function: (define (my-next-append-1 lst1 lst2 res) (cond ((null? lst1) ...) (else (my-next-append-1 (cdr lst1) lst2 ...)))) Fill out the details, and try out your solution. Most likely, you will encounter a couple of problems! Now, do your best to work around these problems, maybe by changing aspects of the templates I have given above. One common problem with iterative solutions and tail recursive functions is that lists will be built in the wrong order. This is due to our use of cons to construct lists, and the fact that cons operates on the front end of the list. The common medicine is to reverse a list, using the function reverse, either on of the input, or on the output.

Exercise 3.5. A list replication function

Write a tail recursive function called replicate-to-length, which in a cyclic way (if necessary) replicates the elements in a list until the resulting list is of certain exact length. The following serves as an example: (replicate-to-length '(a b c) 8) => (a b c a b c a b) (replicate-to-length '(a b c) 2) => (a b) In other words, in (replicate-to-length lst n), take elements out of lst, cyclically if necessary, until you reach n elements.

Examples of recursion: string-merge Slide Annotated slide Contents Index References Textbook

The function string-merge zips two lists of strings to a single string. The lists are not necessarily of equal lengths

Program: The recursive function string-merge. Notice that this function is a general recursive function. The recursive call, emphasized above, is not in a tail position, because of the embedding in string-append.

(define (string-merge str-list-1 str-list-2) (cond ((null? str-list-1) (apply string-append str-list-2)) ((null? str-list-2) (apply string-append str-list-1)) (else (string-append (car str-list-1) (car str-list-2) (string-merge (cdr str-list-1) (cdr str-list-2))))))

Program: An application of string-merge which converts a list of strings to a string with a given separator. This is a typical task in a web program, where a list of elements needs to be aggregated for HTML presentation purposes. Notice the merging of a list of n elements with a list of length n-1. The function make-list is another LAML function; (make-list n el) makes a list of n occurrences of el.

Program: A tail recursive version of string-merge.

(define (string-merge-iter str-list-1 str-list-2) (merge-iter-helper str-list-1 str-list-2 "")) (define (merge-iter-helper str-list-1 str-list-2 res) (cond ((null? str-list-1) (string-append res (apply string-append str-list-2))) ((null? str-list-2) (string-append res (apply string-append str-list-1))) (else (merge-iter-helper (cdr str-list-1) (cdr str-list-2) (string-append res (car str-list-1) (car str-list-2))))))

Examples with recursion: string-of-char-list? Slide Annotated slide Contents Index References Textbook

The function string-of-char-list? is a predicate (a boolean function) that finds out if a string is formed exclusively by characters from a particular alphabet.

Program: The function string-of-char-list? which relies on the tail recursive function string-of-char-list-1?. The function string-of-char-list-1? iterates through the characters in str, via the controlling parameters i and lst.

(define (string-of-char-list? str char-list) (string-of-char-list-1? str char-list 0 (string-length str))) (define (string-of-char-list-1? str char-list i lgt) (if (= i lgt) #t (and (memv (string-ref str i) char-list) (string-of-char-list-1? str char-list (+ i 1) lgt))))

Program: Applications of string-of-char-list?. The function blank-string? determines if a string is formed entirely of white space characters. The function numeric-string? is a predicate that returns true if the string consists exclusively of decimal digits. This is, for instance, useful to check the form input of dates and time in some server-based web applications. The version of numeric-string? in the lib/general.scm of LAML is slightly more general than the version shown above (it allows + or - signs as well, depending on an optional parameter).

;; A list of characters considered as blank space characters (define white-space-char-list (list #\space (as-char 13) (as-char 10) #\tab)) ;; Is the string str empty or blank (consists of white space) (define (blank-string? str) (or (empty-string? str) (string-of-char-list? str white-space-char-list))) ;; Returns if the string str is numeric. ;; More specifically, does str consist exclusively of the ;; ciffers 0 through 9. (define (numeric-string? str) (string-of-char-list? str (list #\0 #\1 #\2 #\3 #\4 #\5 #\6 #\7 #\8 #\9 )))

Exercises Slide Annotated slide Contents Index References

On this page we present an exercise related to recursive processing of lists

Exercise 3.6. Sublists of a list

In this exercise we will program a function front-sublist which returns the first n elements of a list. The signature (the head) of the function should be (front-sublist lst n) where lst is a list and n is a number. As a precondition it can be assumed that lst is a proper list and that n is a non-negative integer. As a postcondition we want to guarantee that the length of the result is n. As an example (front-sublist '(a b c d e) 3) => (a b c) (front-sublist '(a b c d e) 6) => ERROR First, identify the extreme, border cases and be sure that you know how to handle these. Next, program the function with due respect to both the precondition and the postcondition. Next, test the function carefully in a dialogue with your Scheme system. Given the function front-sublist we will program the function sublists, which breaks a proper list into a list of sublists of some given size. As an example (sublists '(a b c d e f) 3) => ((a b c) (d e f)) Program the function sublists with use of front-sublist. Be careful to prepare you solution by recursive thinking. It means that you should be able to break the overall problem into a smaller problem of the same nature, as the original problem. You should feel free to formulate both preconditions and postconditions of the function sublists, such that the existing function front-sublist fits well. Hint: The Scheme function list-tail is probably useful when you program the function sublists. A table can be represented as a list of rows. This is, in fact, the way tables are represented in HTML. The tr tag is used to mark each row; the td tag is used to mark each cell. The table tag is used to mark the overall table. Thus, the list of rows ((a b c) (d e f)) will be marked up as: <table> <tr> <td>a</td> <td>b</td> <td>c</td> </tr> <tr> <td>d</td> <td>e</td> <td>f</td> </tr> </table> Write a Scheme function called table-render that takes a list of rows as input (as returned by the function sublists, which we programmed above) and returns the appropriate HTML rendering of the rows. Use the LAML mirror functions table, tr, and td. Be sure to call the LAML function xml-render to see the textual HTML rendering of the result, as opposed to LAML's internal representation. Notice: During the course we will see better and better ways to program table-render. Nevertheless, it is a good idea already now to program a first version of it.

The concept Hilbert Curve: The Hilbert Curve is a space filling curve that visits every point in a square grid

A hilbert curve of order 5 which is traversed repeatedly to emphasize the maze. The view enforced on you through this picture is an iterative one: We traverse the curve one edge after the other. Needless to tell, this gives a very confusing and complicated understanding of the curve. Below, we will explain the curve in recursive terms. It turns out that this will be key to understanding the curve. Relative to the Scheme program shown later, this curve is produced by the call (hilbert 5 'up) .

The path taken by a Hilbert Curve appears as a sequence - or a certain iteration - of up, down, left, and right.

Reference Recursion - an ECIU material

Building Hilbert Curves of order 1 Slide Annotated slide Contents Index References Textbook

Here we will study the recursive composition of the most simple Hilbert Curve.

A Hilbert Curve of order 1 is composed of four Hilbert Curves of order 0 connected by three connector lines. A Hilbert Curve of order 0 is empty

In the starting point we have a Hilbert Curve of order 0 - that is nothing. It is empty. For illustrative purpose, the empty Hilbert Curve of order 0 is shown as a small circle. We see how four instances (which in the starting point are overlapping in the middle of the picture) are moved to the four corners. Finally the four Curves of order 0 are connected by three connector lines. This makes up a Hilbert Curve of order 1. Relative to the Scheme program shown later, this curve can be produced by the call (hilbert 1 'up) .

Building Hilbert Curves of order 2 Slide Annotated slide Contents Index References Textbook

Here will study the recursive composition of Hilbert Curves in additional details.

A Hilbert Curve of order 2 is composed of four Hilbert Curves of order 1 connected by three connector lines.

In the starting point we have a Hilbert Curve of order 1, as constructed above. We see how four instances (which in the starting point are overlapping in the middle of the picture) are moved to the four corners. Two of them are rotated. Finally the four Curves of order 1 are connected by three connector lines. This makes up a Hilbert Curve of order 2. Relative to the Scheme program shown later, this curve is produced by the call (hilbert 2 'up) .

Building Hilbert Curves of order 3 Slide Annotated slide Contents Index References Textbook

In the same way we made a Hilbert Curve of order 2, we will here see how a Hilbert Curve of order 3 is made.

A Hilbert Curve of order 3 is composed of four Hilbert Curves of order 2 connected by three connector lines.

In the starting point we have a Hilbert Curve of order 2, as constructed above. We see how four instances (which in the starting point are overlapping in the middle of the picture) are moved to the four corners. Two of them are rotated. Finally the four Curves of order 2 are connected by three connector lines. This makes up a Hilbert Curve of order 3. Relative to the Scheme program shown later, this curve can be produced by the call (hilbert 3 'up) .

Building Hilbert Curves of order 4 Slide Annotated slide Contents Index References Textbook

In the same way we made a Hilbert Curve of order 3, we will here see how a Hilbert Curve of order 4 is made. This is the final development along these lines in this material.

A Hilbert Curve of order 4 is composed of four Hilbert Curves of order 3 connected by three connector lines.

In the starting point we have a Hilbert Curve of order 3, as constructed above. We see how four instances (which in the starting point are overlapping in the middle of the picture) are moved to the four corners. Two of them are rotated. Finally the four Curves of order 3 are connected by three connector lines. This makes up a Hilbert Curve of order 4. Relative to the Scheme program shown later, this curve is produced by the call (hilbert 4 'up) .

A program making Hilbert Curves Slide Annotated slide Contents Index References Textbook

Given our understanding of Hilbert Curves obtained from the previous pages, we will now study a computer program that generates Hilbert Curves of order n, where n is any non-negative number.

We will here discuss a concrete program which draws Hilbert Curves of order n

Program: The function hilbert programmed in Scheme as a functional program. The function returns the path of the Hilbert Curver of order n. The parameter turn determines the rotation of the curve. In the top level call we ask for an upward Hilbert Curve: As an example, (hilbert 3 'up) produces an upward Hilbert Curve of order 3. The red fragments are responsible for all line drawing. The blue fragments represent all the recursive calls of the hilbert function. Finally, the green fragment represent the level 0 'basis' case. The level 0 case returns the empty Hilbert Curve, which is literally empty (no drawing at all - no contribution to the resulting path). What does it mean that the the program is a functional program? Well, it basically means that hilbert returns a value which can be rendered somehow by another function or procedure. The value returned is a path, composed by concat-path. The hilbert function does not carry out any action itself.

(define (hilbert n turn) (cond ((= n 0) (empty-hilbert-curve)) ((> n 0) (cond ((eq? turn 'up) (concat-path (hilbert (- n 1) 'right) (up-line) (hilbert (- n 1) 'up) (right-line) (hilbert (- n 1) 'up) (down-line) (hilbert (- n 1) 'left) )) ((eq? turn 'left) (concat-path (hilbert (- n 1) 'down) (left-line) (hilbert (- n 1) 'left) (down-line) (hilbert (- n 1) 'left) (right-line) (hilbert (- n 1) 'up))) ((eq? turn 'right) (concat-path (hilbert (- n 1) 'up) (right-line) (hilbert (- n 1) 'right) (up-line) (hilbert (- n 1) 'right) (left-line) (hilbert (- n 1) 'down))) ((eq? turn 'down) (concat-path (hilbert (- n 1) 'left) (down-line) (hilbert (- n 1) 'down) (left-line) (hilbert (- n 1) 'down) (up-line) (hilbert (- n 1) 'right))) ))))

Program: The complete Hilbert programs including SVG details.

Program: A simple Scheme path library developed for SVG.

References SVG SVG Tutorial

It is sometimes necessary to escape from a deep expression, for instance in an exceptional case We are interested in a primitive which allows us to control the remaining part of a calculation - a so-called continuation.

Exit or exception mechanism: The need to abandon some deep evaluation Continuation Capturing of continuations Exploring new control mechanisms by use of continuations

Scheme support first class continuations dressed as functions

The catch and throw idea Slide Annotated slide Contents Index References Textbook

Catch and throw provides for an intuitively simple escape mechanism on functional ground

Syntax:

(catch id catch-expr)

Syntax:

(throw id throw-expression)

Scheme does not support catch and throw Rather Scheme supports a much more powerful mechanisms based on continuations

References Common Lisp the Language, 2nd Edition. Dynamic Non-local exists (Common Lisp)

A catch and throw example Slide Annotated slide Contents Index References Textbook

We now give a Common Lisp like example of catch and throw.

Exit from a list length function in case it discovers a non-empty tail of the list

Program: An example using catch and throw. Please notice that the example is not a proper Scheme program. Catch and throw are not defined in Scheme.

(define (list-length lst) (catch 'exit (letrec ((list-length1 (lambda (lst) (cond ((null? lst) 0) ((pair? lst) (+ 1 (list-length1 (cdr lst)))) (else (throw 'exit 'improper-list)))))) (list-length1 lst))))

Catch and throw are not available in standard Scheme

The intuition behind continuations Slide Annotated slide Contents Index References Textbook

The concept continuation: A continuation of the evaluation of an expression E in a surrounding context C represents the future of the computation, which waits for, and depends on, the value of E

Table. An intuitive understanding of continuations of an expression in some context.

Context C and expression E Intuitive continuation of E in C (+ 5 (* 4 3)) The adding of 5 to the value of E (cons 1 (cons 2 (cons 3 '()))) The consing of 3, 2 and 1 to the value of E (define x 5) (if (= 0 x) 'undefined (remainder (* (+ x 1) (- x 1)) x)) The multiplication of E by x - 1 followed by a division by x

Being more precise Slide Annotated slide Contents Index References Textbook

Instead of relying of an informal understanding of continuations we will now introduce lambda expressions that represent the continuations.

We can form a lambda expression that to some degree represents a continuation

Table. A more precise notation of the continuations of E

Context C and expression E The continuation of E in C (+ 5 (* 4 3)) (lambda (e) (+ 5 e)) (cons 1 (cons 2 (cons 3 '()))) (lambda (e) (cons 1 (cons 2 (cons 3 e)))) (define x 5) (if (= 0 x) 'undefined (remainder (* (+ x 1) (- x 1)) x)) (lambda (e) (remainder (* e (- x 1)) x))

The capturing of continuations Slide Annotated slide Contents Index References Textbook

It is now time to introduce the Scheme primitive that allows us to capture a continuation.

Scheme provides a primitive that captures a continuation of an expression E in a context C The primitive is called call-with-current-continuation, or call/cc as a short alias call/cc takes a parameter, which is a function of one parameter. The parameter of the function is bound to the continuation, and the body of the function is E

Table. Use of call/cc and capturing of continuations.

Context C and the capturing (+ 5 (call/cc (lambda (e) (* 4 3)) )) (cons 1 (cons 2 (cons 3 (call/cc (lambda (e) '()) )))) (define x 5) (if (= 0 x) 'undefined (remainder (* (call/cc (lambda (e) (+ x 1)) ) (- x 1)) x))

Capturing, storing, and applying continuations Slide Annotated slide Contents Index References Textbook

We here show capturing, imperative assignment, and a subsequent application of a continuation

Table. Capturing and applying continuations. The captured continuations are stored in a global variable. The application of the continuation is shown in the third column, and the result of the application of the continuation is shown in the fourth column.

Context C and expression E Value of C Application of continuation Value (+ 5 (call/cc (lambda (e) (set! cont-remember e) (* 4 3)))) 17 (cont-remember 3) 8 (cons 1 (cons 2 (cons 3 (call/cc (lambda (e) (set! cont-remember e) '()))))) (1 2 3) (cont-remember '(7 8)) (1 2 3 7 8) (define x 5) (if (= 0 x) 'undefined (remainder (* (call/cc (lambda (e) (set! cont-remember e) (+ x 1) )) (- x 1)) x)) 4 (cont-remember 3) 2

Use of continuations for escaping purposes Slide Annotated slide Contents Index References Textbook

We here illustrate applications of the continuations for escaping purposes

Table. Capturing and use of a continuation for escaping purposes

Context C, capturing, and escape call Value (+ 5 (call/cc (lambda (e) (* 4 (e 10)))) ) 15 (cons 1 (call/cc (lambda (e) (cons 2 (cons 3 (e 'x))))) ) (1 . x) (define x 5) (if (= 0 x) 'undefined (call/cc (lambda (e) (remainder (* (+ x 1) (- x (e 111))) x))) ) 111

Practical example: Length of an improper list Slide Annotated slide Contents Index References Textbook

The length of an improper list is undefined We chose to return the symbol improper-list if list-length encounters an improper list This example is similar to the catch and throw example shown earlier in this section

Program: The function list-length, which returns the symbol 'improper-list in case it encounters an improper list.

(define (list-length l) (call-with-current-continuation (lambda (do-exit) (letrec ((list-length1 (lambda (l) (cond ((null? l) 0) ((pair? l) (+ 1 (list-length1 (cdr l)))) (else (do-exit 'improper-list)))))) (list-length1 l))) ))

Practical example: Searching a binary tree Slide Annotated slide Contents Index References Textbook

Searching a binary tree involves a recursively defined tree traversal If we find the node we are looking for it is convenient to throw the out of the tree traversal

Program: A tree search function which uses a continuation found if we find what we search for. Notice that this examples requires the function subtree-list, in order to work. The function returns #f in case we do not find node we are looking for. Notice that it makes sense in this example to have both the if expression and the #f value in sequence!

(define (find-in-tree tree pred) (call-with-current-continuation (lambda (found) (letrec ((find-in-tree1 (lambda (tree pred) (if (pred tree) (found tree) (let ((subtrees (subtree-list tree))) (for-each (lambda (subtree) (find-in-tree1 subtree pred)) subtrees))) #f))) (find-in-tree1 tree pred))) ))

Chapter 3: Name binding, Recursion, Iteration, and Continuations
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: July 2, 2013, 09:15:04