In the same style as our coverage of lists in Chapter 45 we will in this chapter discuss generic interfaces and classes for dictionaries. This covers the high-level concept of associative arrays and the low-level concept of hash tables.

46.1 Overview of Generic Dictionaries in C# 46.4 Sample use of class Dictionary<K,V> 46.2 The interface IDictionary<K,V> 46.5 Notes about Dictionary Classes 46.3 Overview of the class Dictionary<K,V> 46.6 Time complexity overview: Dictionary classes

 

46.1.  Overview of Generic Dictionaries in C#
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

A dictionary is a data structure that maps keys to values. A given key can have at most one value in the dictionary. In other words, the key of a key-value pair must be unique in the dictionary. A given value can be associated with many different keys.

At the conceptual level, a dictionary can be understood as an associative array (see Section 19.2) or as a collection of key-value pairs. In principle the collection classes from Chapter 45 can be used as an underlying representation. It is, however, convenient to provide a specialized interface to dictionaries which sets them apart from collections in general. In addition we often need good performance (fast lookup), and therefore it is more than justified to have special support for dictionaries in the C# libraries.

Figure 46.1 gives an overview of the generic interfaces and the generic classes of dictionaries. The figure is comparable with Figure 45.1 for collections. As such, the white boxes represent interfaces and the grey boxes represent classes. As it appears from Figure 46.1 we model dictionaries as IEnumerables (see Section 45.2) and ICollections (see Section 45.3) at the highest levels of abstractions. From the figure we can directly read that a dictionary is a ICollection of KeyValuePairs. (The is a relation is discussed in Section 25.2).

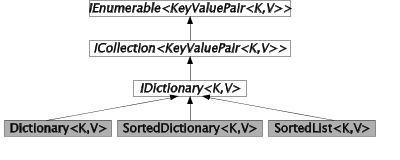
Figure 46.1    The class and interface inheritance tree related to Dictionaries

The symbol K stands for the type of keys, and the symbol V stands for the type of values. KeyValuePair<K,V> is a simple struct that aggregates a key and a value to a single object.

Dictinonary<K,V> is implemented in terms of a hashtable that maps objects of type K to objects of type V. SortedDictinonary<K,V> relies on binary search trees. SortedList<K,V> is based on a sorted arrays. More details can be found in Section 46.5. In Section 46.6 we review the time complexities of the operations of the three dictionary classes shown above.

46.2.  The interface IDictionary<K,V>
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

From Figure 46.1 we see that the interface IDictionary<K,V> is a subinterface of ICollection<KeyValuePair<K,V>>. We gave an overview of the generic interface ICollection<T> in Section 45.3. Because of this subinterface relationships we know that it is possible to use the operations Contains, Add, Remove on objects of type KeyValuePair<K,V>. Notice, however, that these operations are rather inconvenient because the generic class KeyValuePair is involved. Instead of Add(new KeyValuePair(k,v)) we prefer another overload of Add, namely Add(k,v). The mentioned operations Contains, Add, and Remove on KeyValuePairs are available in the Dictionary classes of Figure 46.1, but they are degraded to explicit interface implementations (see Section 31.8).

The following provides an overview of the operations in IDictionary<K,V>:

The operations prescribed in ICollection<KeyValuePair<K,V>> The operations prescribed in IEnumerable<KeyValuePair<K,V>> V this[K key]     - both getter and setter; the setter adds or mutates void Add(K key, V value)     - only possible if key is not already present bool Remove(K key) bool ContainsKey(K key) bool TryGetValue(K key, out V value) ICollection<K>Keys     - getter ICollection<V>Values     - getter

V this[K key] is an indexer via which we can set and get a value of a given key by means of array notation (see Section 19.1). If dict is declared of type IDictionary<K,V> then the indexer notation allows us to express

   valVar = dict[someKey];
   dict[someKey] = someValue;

The first line accesses (gets/reads) the value associated with someKey. If no value is associated with someKey an KeyNotFoundException is thrown. The second line adds (sets/writes) an association between someKey and someValue to dict. If the association is already in the dictionary, the setter mutates the value associated with someKey.

The operation Add(key,value) adds an association between key and value to the dictionary. If the key is already associated with (another) value in the dictionary an ArgumentException will be thrown.

Remove(key) removes the association of key and its associated value. Via the value returned, the Remove operation signals if the removal was successful. Remove returns false if key is not present in the dictionary.

ContainsKey(key) tells if key is present in the dictionary.

The operation call TryGetValue(key, valueVar) accesses the value of key, and it passes the value via an output parameter (see Section 20.7). If no value is associated with key, the default value of type V (see Section 12.3) is passed back in the output parameter. This method is added of convenience. Alternatively, the indexer can be used in combination with ContainsKey.

The properties Keys and Values return collections of the keys and the values of a dictionary.

46.3.  Overview of the class Dictionary<K,V>
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

The generic class Dictionary<K,V> is based on hashtables. Dictionary<K,V> implements the interface IDictionary<K,V> as described in Section 46.2. Almost all methods and properties of Dictionary<K,V> are prescribed by the direct and indirect interfaces of the class. Here is an overview of the most important operations in Dictionary<K,V>.

Constructors Dictionary(),   Dictionary(IDictionary<K,V>),   Dictionary(IEqualityComparer<K>),   Dictionary(int),   and more Value addition Add(K, V), this[K] = V         if K is not already in the dictionary Value mutation this[K] = V         if K is already in the dictionary Element removal Remove(K),   Clear() Value access this[K],   Values,   TryGetValue(K, out V) Key access Keys Boolean queries ContainsKey(K),   ContainsValue(V) Others Count Comparer

As it appears from the discussion of dictionaries above, it is necessary that two keys can be compared for equality. The equality comparison can be provided in several different ways. It is possible to pass an EqualityComparer object to the Dictionary constructor. Alternatively, we fall back on the default equality comparer of the key type K. The property Comparer of class Dictionary<K,V> returns the comparer used for key comparison in the current dictionary. See also the discussion of equality comparison in Section 42.9.

As already mentioned, a dictionary is implemented as a hash table. A hash table provides very fast access to the a value of a given key. Under normal circumstances - and with a good hash function - the run times of the access operations are constant (the run times do not depend on the size of the dictionary). Thus, the time complexity is O(1). Please consult Section 46.6 for more details on the efficiency of the dictionary operations.

46.4.  Sample use of class Dictionary<K,V>
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

In this section we will illustrate the use of dictionaries with a simple example. We go for a dictionary that maps objects of type Person to objects of type BankAccount. Given a Person object (the key) we wish to have efficient access to the person's BankAccount (the value).

The class Person is similar to Program 20.3. The class BankAccount is similar to Program 25.1, but without an owner. (The owner of a bank account is in this example handled via the bankMap dictionary). The exact versions of Person and BankAccount, as used in the dictionary example, can be accessed via the accompanying slide page, or via the program index of this lecture.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

using System;
using System.Collections.Generic;

class DictionaryDemo{

  public static void Main(){

    IDictionary<Person, BankAccount> bankMap =                       
      new Dictionary<Person,BankAccount>(new PersonComparer());      

    // Make bank accounts and person objects
    BankAccount ba1 =  new BankAccount(0.01),  
                ba2 =  new BankAccount(0.02),  
                ba3 =  new BankAccount(0.03),
                ba4 =  new BankAccount(0.04);

    Person p1 = new Person("Kurt"),  
           p2 = new Person("Maria"),
           p3 = new Person("Francoi");

    ba1.Deposit(100); ba2.Deposit(200); ba3.Deposit(300);   
                                                            
    // Populate the bankMap: 
    bankMap.Add(p1, ba1);                                   
    bankMap.Add(p2, ba2);                                   
    bankMap.Add(p3, ba3);                                   
    ReportDictionary("Initial map", bankMap);

    // Print Kurt's entry in the map:
    Console.WriteLine("{0}\n", bankMap[p1]);                

    // Mutate Kurt's entry in the map
    bankMap[p1] = ba4;                                      
    ReportDictionary("bankMap[p1] = ba4;", bankMap);

    // Mutate Maria's entry in the map. PersonComparer crucial!
    ba4.Deposit(400);
    bankMap[new Person("Maria")] = ba4;                     
    ReportDictionary("ba4.Deposit(400);  bankMap[new Person(\"Maria\")] = ba4;", bankMap);

    // Add p3 yet another time to the map
    // Run-time error: An item with the same key has already been added.
/*  bankMap.Add(p3, ba1);
    ReportDictionary("bankMap.Add(p3, ba1);", bankMap); 
 */

    // Try getting values of some given keys
    BankAccount ba1Res = null,
                ba2Res = null;
    bool res1 = false,
         res2 = false;
    res1 = bankMap.TryGetValue(p2, out ba1Res);                        
    res2 = bankMap.TryGetValue(new Person("Anders"), out ba2Res);          
    Console.WriteLine("Account: {0}. Boolean result {1}", ba1Res, res1);   
    Console.WriteLine("Account: {0}. Boolean result {1}", ba2Res, res2);   
    Console.WriteLine();

    // Remove an entry from the map
    bankMap.Remove(p1);                                                    
    ReportDictionary("bankMap.Remove(p1);", bankMap);

    // Remove another entry - works because of PersonComparer
    bankMap.Remove(new Person("Francoi"));                                   
    ReportDictionary("bankMap.Remove(new Person(\"Francoi\"));", bankMap);   
  }

  public static void ReportDictionary<K, V>(string explanation,              
                                            IDictionary<K,V> dict){          
    Console.WriteLine(explanation);
    foreach(KeyValuePair<K,V> kvp in dict)
      Console.WriteLine("{0}: {1}", kvp.Key, kvp.Value);
    Console.WriteLine(); 
  }
}

public class PersonComparer: IEqualityComparer<Person>{                      

  public bool Equals(Person p1, Person p2){   
    return (p1.Name == p2.Name);                                             
  }                                                                          

  public int GetHashCode(Person p){
    return p.Name.GetHashCode();
  }
}

In line 8-9 we make the dictionary bankMap of type Dictionary<Person,BankAccount>. We pass an instance of class PersonComparer, see line 76-86, which implements IEqualityComparer<Person>. In line 11-19 we make sample BankAccount and Person objects, and in line 24-26 we populate the dictionary bankMap.

In line 30 we see how to access the bank account of person p1 (Kurt). We use the provided indexer of the dictionary. In line 33 we mutate the bankMap: Kurt's bank account is changed from the one referenced by ba1 to the one referenced by ba4. In line 38 we mutate Maria's bank account in a similar way. Notice, however, that that the relative weak equality of Person objects (implemented in class PersonComparer) implies that the new person("Maria") in line 38 is equal to the person referenced by p2, and therefore line 38 mutates the dictionary entry for Maria.

In line 43 we attempt add yet another entry for Francoi. This is illegal because there is already an entry for Francoi in the dictionary. If the comments around line 43 are removed, a run time error will occur.

In line 52-53 we illustrate TryGetValue. First, in line 52, we attempt to access Maria's account. The out parameter baRes1 is assigned to Maria's account and true is returned from the method. In line 53 we attempt to access the account of a brand new Person object, which has no bank account in the dictionary. null is returned through ba2Res, and false is returned from the method.

Finally, in line 58-64 we remove entries from the dictionary by use of the Remove method. First Kurt's entry is removed after which Francoi's entry is removed.

The output of the program is shown in Listing 46.2 (only on web).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

Initial map
Person: Kurt : The account holds 100 kroner
Person: Maria : The account holds 200 kroner
Person: Francoi : The account holds 300 kroner

The account holds 100 kroner

bankMap[p1] = ba4;
Person: Kurt : The account holds 0 kroner
Person: Maria : The account holds 200 kroner
Person: Francoi : The account holds 300 kroner

ba4.Deposit(400);  bankMap[new Person("Maria")] = ba4;
Person: Kurt : The account holds 400 kroner
Person: Maria : The account holds 400 kroner
Person: Francoi : The account holds 300 kroner

Account: The account holds 400 kroner. Boolean result True
Account: . Boolean result False

bankMap.Remove(p1);
Person: Maria : The account holds 400 kroner
Person: Francoi : The account holds 300 kroner

bankMap.Remove(new Person("Francoi"));
Person: Maria : The account holds 400 kroner

46.5.  Notes about Dictionary Classes
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

As can be seen from Figure 46.1 several different generic classes implement the IDictionary<K,V> interface. Dictionary<K,V>, as discussed in Section 46.3 and Section 46.4 is based on a hash table representation. SortedDictionary<K,V> is based on a binary tree, and (as the name signals) SortedList<K,V> is based on an array of key/value pairs, sorted by keys.

The following provides an itemized overview of the three generic dictionary classes.

Class Dictionary<K,V> Based on a hash table Requires that the keys in type K can be compared by an Equals operation Key values should not be mutated The efficiency of class dictionary relies on a good hash function for the key type K Consider overriding the method GetHashCode in class K A dictionary is enumerated in terms of the struct KeyValuePair<K,V> Class SortedDictionary<K,V> Based on a binary search tree Requires an IComparer for keys of type K - for ordering purposes Provided when a sorted dictionary is constructed Class SortedList<K,V> Based on a sorted collection of key/value pairs A resizeable array Requires an IComparer for keys, just like SortedDictionary<K,V>. Requires less memory than SortedDictionary<K,V>.

When you have to chose between the three dictionary classes the most important concern is the different run time characteristics of the operations of the classes. The next section provides an overview of these.

46.6.  Time complexity overview: Dictionary classes
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

We will now review the time complexities of the most important dictionary operations. This is done in the same way as we did for collections (lists) in Section 45.17. We will assume that we work on a dictionary that holds n entries of key/value pairs.

As noticed in Section 46.5 an object of type Dictionary<K,V> is based on hash tables. Eventually, it will be necessary to enlarge the hashtable to hold new elements. It is good wisdom to enlarge the hashtable when it becomes half full. The O(1) or O(n) time complexity for Add reflects that a work proportional to n is needed when it becomes necessary to enlarge the hash table.

Most operations on the binary tree representation of SortedDictionary<K,V> are logarithmic in n. The only exception (among the operations listed in the table) is ContainsValue, which in the worst case requires a full tree traversal.

In SortedList<K,V> the indexer is efficient, O(log n) when an existing item is mutated. If use of the indexer causes addition of a new entry, the run time is the same as the run time of Add. Adding elements to a sorted list requires, in average, that half of the elements are pushed towards the end of the list in order to create free space for the new entry. This is an O(n) operation. Remove is symmetric, pulling elements towards the beginning of the list, and therefore also O(n). ContainsKey is efficient because we can do binary search on the sorted list. ContainsValue requires linear search, and therefore it is an O(n) operation.

Given the table in Table 46.1 it is tempting to conclude that Dictionary<K,V> is the best of the three classes. Notice, however, that the difference between a constant run time c1 and c2 log(n) is not necessarily significant. If the constant c1 is large and the constant c2 is small, the binary tree may be an attractive alternative. Furthermore, we know that the hashtable will be slow when it is almost full. In that case more and more collisions can be expected. At some point in time the hash table will stop working if it is not resized. This is not an issue if we work with balanced binary trees. Finally, the hashtable depends critically on a good hash function, preferable programmed specifically for the key type K. This is not an issue if we use binary trees.