   | Collection Classes |
| A complete PDF version of the text book is now available. The PDF version is an almost complete subset of the HTML version (where only a few, long program listings have been removed). See here. |
   | Collection Classes |
| A complete PDF version of the text book is now available. The PDF version is an almost complete subset of the HTML version (where only a few, long program listings have been removed). See here. |
In this chapter we will study different list interfaces and classes.
45.1. Overview of Generic Collections in C#
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We start by showing a type hierarchy of list-related types. The white boxes in Figure 45.1 are interfaces and the grey boxes are classes.
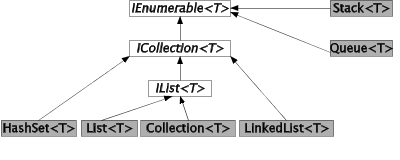
| Figure 45.1 The class and interface inheritance tree related to Lists |
All interfaces and classes seen in Figure 45.1, apart from Stack<T> and Queue<T>, will be discussed in the forthcoming sections of the current chapter.
The class System.Array (see Section 28.2 ) which conceptually is the superclass of all native array types in C#, also implements the generic interfaces IList<T>. Notice, however, that Array 's implementation of IList<T> is carried out by special means, and that it does not show up in the usual C# documentation. A more detailed discussion of the Array class is carried out in Section 47.1.
Version 3.5 of the .NET Framework contains a class, HashSet<T>, that supports the mathematical set concept. As such, it is similar to the class Set<T>, which we used as example for introduction of generic types in Section 42.1. HashSet<T> is, however, much more efficient than Set<T>.
45.2. The Interface IEnumerable<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
At the most general level of Figure 45.1 traversability is emphasized. This covers the ability to step through all elements of a collection. The interface IEnumerable<T> announces one parameterless method called GetEnumerator. The type parameter T is the type of the elements in the collection.
|
As the name indicates, GetEnumerator returns an enumerator, which offers the following interface:
|
We have discussed the non-generic versions of both interfaces in Section 31.6. An IEnumerator object is used as the basis of traversal in a foreach loop.
Without access to an IEnumerator object it would not be possible to traverse the elements of a collection in a foreach loop. You do not very often use the GetEnumerator operation explicitly in your own program, but you most probably rely on it implicitly! The reason is that many of your collections are traversed, from one end to the other, by use of foreach. The foreach control structure would not work without the operation GetEnumerator. As you can see from Figure 45.1 all of our collections implement the interface IEnumerable<T> and hereby they provide the operation GetEnumerator.
It is worth noticing that an object of type IEnumerator<T> does not support removal of elements from the collection. In C# it is therefore not allowed to remove elements during traversal of a collection in a foreach loop. In the Java counterpart to IEnumerator<T> (called Iterator in Java), there is a remove method. The remove method can be called once for each step forward in the collection. remove is an optional operation in the Java Iterator interface. Consequently, removal of elements is not necessarily supported by all implementations of the Java Iterator interface.
45.3. The Interface ICollection<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
At the next level of Figure 45.1 we encounter the ICollection<T> interface. It can be summarized as follows.
|
In addition to traversability, elements of type T can be added to and removed from objects of type ICollection<T>. At this level of abstraction, it is not specified where in the collection an element is added. As listed about, a few other operations are supported: Membership testing (Contains), resetting (Clear), copying of the collection to an array (CopyTo), and measuring of size (Count). Some collections cannot be mutated once they have been created. The IsReadOnly property allows us to find out if a given ICollection object is a read only collection.
45.4. The Interface IList<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
At the next level of interfaces in Figure 45.1 we meet IList<T>. This interface prescribes random access to elements.
|
In addition to ICollection<T>, the type IList<T> allows for indexed access to the T elements. The first mentioned operation (this) is an indexer, and IndexOf is its inverse operation. (See Chapter 19 for a general discussion of indexers). In addition, IList<T> has operations for inserting and removing elements at given index positions.
45.5. Overview of the class Collection<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We now encounter the first class in the collection hierarchy, namely Collection<T>. Most interfaces and classes discussed in this chapter belong to the namespace System.Collections.Generic, but of some odd reason the class Collection<T> belongs to System.Collections.ObjectModel.
As can be seen from Figure 45.1 the generic class Collection<T> implements the generic interface IList<T>. As such it supports all the operations of the three interfaces we discussed in Section 45.2 - Section 45.4. As it appears from Figure 45.1 the generic class List<T> implements the same interface. It turns out that Collection<T> is a minimal class which implements the three interfaces, and not much more. As we will see in Section 45.9, List<T> has many more operations, most of which are not prescribed by the interfaces it implement.
Basically, an instance of Collection<T> supports indexed access to its elements. Contrary to arrays, however, there is no limit on the number of elements in the collection. The generic class Collection<T> has another twist: It is well suited as a superclass for specialized (non-generic) collections. We will see why and how in Section 45.7.
Below we list the complete, public interface of Collection<T>:
|
Collection initializers are new in C# 3.0. Instead of initializing a collection via an IList, typically an array, such as in
Collection<int> lst = new Collection<int>(new int[]{1, 2, 3, 4});it is possible in C# 3.0 to make use of collection initializers:
Collection<int> lst = new Collection{1, 2, 3, 4};A collection initializer uses the Add method repeatedly to insert the elements within {...} into an empty list.
Collection initializers are often used in concert with object initializers, see Section 18.4, to provide for smooth creation of collection of objects, which are instances of our own types.
You may be interested to know details of the actual representation (data structure) used internally in the generic class Collection<T>. Is it an array? Is it a linked list? Or is it something else, such as a mix of arrays and lists, or a tree structure? Most likely, it is a resizeable array. Notice however that from an object-oriented programming point of view (implying encapsulation and visibility control) it is inappropriate to ask such a question. It is sufficient to know about the interface of Collection<T> together with the time complexities of the involved operations. (As an additional remark, the source code of the C# libraries written by Microsoft is not generally available for inspection. Therefore we cannot easily check the representation details of the class). The interface of Collection<T> includes details about the execution times of the operations of Collection<T> relative to the size of a collection. We deal with timing issues of the operations in the collection classes in Section 45.17.
45.6. Sample use of class Collection<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Let us now write a program that shows how to use the central operations in Collection<T>. In Program 45.1 we use an instance of the constructed class Collection<char>. Thus, we deal with a collection of character values. It is actually worth noticing that we in C# can deal with collections of value types (such as Collection<char>) as well as collections of reference types (such as Collection<Point>).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | using System;
using System.Collections.ObjectModel;
using System.Collections.Generic;
class BasicCollectionDemo{
public static void Main(){
// Initialization - use of a collection initializer. After that add 2 elements.
IList<char> lst = new Collection<char>{'a', 'b', 'c'};
lst.Add('d'); lst.Add('e');
ReportList("Initial List", lst);
// Mutate existing elements in the list:
lst[0] = 'z'; lst[1]++;
ReportList("lst[0] = 'z'; lst[1]++;", lst);
// Insert and push towards the end:
lst.Insert(0,'n');
ReportList("lst.Insert(0,'n');", lst);
// Insert at end - with Insert:
lst.Insert(lst.Count,'x'); // equivalent to lst.Add('x');
ReportList("lst.Insert(lst.Count,'x');", lst);
// Remove element 0 and pull toward the beginning:
lst.RemoveAt(0);
ReportList("lst.RemoveAt(0);", lst);
// Remove first occurrence of 'c':
lst.Remove('c');
ReportList("lst.Remove('c');", lst);
// Remove remaining elements:
lst.Clear();
ReportList("lst.Clear(); ", lst);
}
public static void ReportList<T>(string explanation, IList<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.Write("{0, 3}", el);
Console.WriteLine(); Console.WriteLine();
}
} | |||
|
The program shown above explains itself in the comments, and the program output in Listing 45.2 is also relatively self-contained. Notice the use of the collection initializer in line 9 of Program 45.1. As mentioned in Section 45.5 collection initializers have been introduced in C# 3.0. In earlier versions of C# it was necessary to initialize a collection by use or an array initializer (see the discussion of Program 6.7) via the second constructor mentioned above.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | Initial List
a b c d e
lst[0] = 'z'; lst[1]++;
z c c d e
lst.Insert(0,'n');
n z c c d e
lst.Insert(lst.Count,'x');
n z c c d e x
lst.RemoveAt(0);
z c c d e x
lst.Remove('c');
z c d e x
lst.Clear(); | |||
|
We make the following important observations about the operations in Collection<T>:
|
45.7. Specialization of Collections
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Let us now assume that we wish to make our own, specialized (non-generic) collection class of a particular type of objects. Below we will - for illustrative purposes - write a class called AnimalFarm which is intended to hold instances of class Animal. It is reasonable to program AnimalFarm as a subclass of an existing collection class. In this section we shall see that Collection<Animal> is a good choice of superclass of AnimalFarm.
The class AnimalFarm depends on the class Animal. You are invited to take a look at class Animal via the accompanying slide . We do not include class Animal here because it does not add new insight to our interests in collection classes. The four operations of class AnimalFarm are shown below.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | using System;
using System.Collections.ObjectModel;
public class AnimalFarm: Collection<Animal>{
protected override void InsertItem(int i, Animal a){
base.InsertItem(i,a);
Console.WriteLine("**InsertItem: {0}, {1}", i, a);
}
protected override void SetItem(int i, Animal a){
base.SetItem(i,a);
Console.WriteLine("**SetItem: {0}, {1}", i, a);
}
protected override void RemoveItem(int i){
base.RemoveItem(i);
Console.WriteLine("**RemoveItem: {0}", i);
}
protected override void ClearItems(){
base.ClearItems();
Console.WriteLine("**ClearItems");
}
} | |||
|
It is important to notice that the four highlighted operations in Program 45.3 are redefinitions of virtual, protected methods in Collection<Animal>. Each of the methods activate the similar method in the superclass (this is method combination). In addition, they reveal on standard output that the protected method has been called. A more realistic example of class AnimalFarm will be presented in Program 45.6.
The four operations are not part of the client interface of class AnimalFarm. They are protected operations. The client interface of AnimalFarm is identical to the public operations inherited from Collection<Animal>. It means that we use the operations Add, Insert, Remove etc. on instances of class AnimalFarm.
We should now understand the role of the four protected operations InsertItem, RemoveItem, SetItem, and ClearItems relative to the operations in the public client interface. Whenever an element is inserted into a collection, the protected method InsertItem is called. Both Add and Insert are programmed by use of InsertItem. Similarly, both Remove and RemoveAt are programmed by use of RemoveItem. And so on. We see that the major functionality behind the operations in Collection<T> is controlled by the four protected methods InsertItem, RemoveItem, SetItem, and ClearItems.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | using System;
using System.Collections.ObjectModel;
class App{
public static void Main(){
AnimalFarm af = new AnimalFarm();
// Populating the farm with Add
af.Add(new Animal("elephant"));
af.Add(new Animal("giraffe"));
af.Add(new Animal("tiger"));
ReportList("Adding elephant, giraffe, and tiger with Add(...)", af);
// Additional population with Insert
af.Insert(0, new Animal("dog"));
af.Insert(0, new Animal("cat"));
ReportList("Inserting dog and cat at index 0 with Insert(0, ...)", af);
// Mutate the animal farm:
af[1] = new Animal("herring", AnimalGroup.Fish, Sex.Male);
ReportList("After af[1] = herring", af);
// Remove tiger
af.Remove(new Animal("tiger"));
ReportList("Removing tiger with Remove(...)", af);
// Remove animal at index 2
af.RemoveAt(2);
ReportList("Removing animal at index 2, with RemoveAt(2)", af);
// Clear the farm
af.Clear();
ReportList("Clear the farm with Clear()", af);
}
public static void ReportList<T>(string explanation, Collection<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.WriteLine("{0, 3}", el);
Console.WriteLine(); Console.WriteLine();
}
} | |||
|
Take a close look at the output of Program 45.4 in Listing 45.5. The output explains the program behavior.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | **InsertItem: 0, Animal: elephant **InsertItem: 1, Animal: giraffe **InsertItem: 2, Animal: tiger Adding elephant, giraffe, and tiger with Add(...) Animal: elephant Animal: giraffe Animal: tiger **InsertItem: 0, Animal: dog **InsertItem: 0, Animal: cat Inserting dog and cat at index 0 with Insert(0, ...) Animal: cat Animal: dog Animal: elephant Animal: giraffe Animal: tiger **SetItem: 1, Animal: herring After af[1] = herring Animal: cat Animal: herring Animal: elephant Animal: giraffe Animal: tiger **RemoveItem: 4 Removing tiger with Remove(...) Animal: cat Animal: herring Animal: elephant Animal: giraffe **RemoveItem: 2 Removing animal at index 2, with RemoveAt(2) Animal: cat Animal: herring Animal: giraffe **ClearItems Clear the farm with Clear() | |||
|
45.8. Specialization of Collections - a realistic example
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
The protected methods in class AnimalFarm, as shown in Section 45.7, did only reveal if/when the protected methods were called by other methods. In this section we will show a more realistic example that redefines the four protected methods of Collection<T> in a more useful way.
In the example we program the following semantics of the insertion and removal operations of class AnimalFarm:
In addition, we add a GetGroup operation to AnimalFarm, which returns a collection (an sub animal farm) of all animals that belongs to a given group (such as all birds).
The class Animal has not been changed, and it still available via accompanying slide.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | using System;
using System.Collections.ObjectModel;
public class AnimalFarm: Collection<Animal>{
// Auto insert animal of opposite sex
protected override void InsertItem(int i, Animal a){
if(a.Sex == Sex.Male){
base.InsertItem(i,a);
base.InsertItem(i, new Animal(a.Name, a.Group, Sex.Female));
} else {
base.InsertItem(i,a);
base.InsertItem(i,new Animal(a.Name, a.Group, Sex.Male));
}
}
// Prevent removal
protected override void RemoveItem(int i){
Console.WriteLine("[Removal denied]");
}
// Prevent clearing
protected override void ClearItems(){
Console.WriteLine("[Clearing denied]");
}
// Return all male animals in a given group
public AnimalFarm GetGroup(AnimalGroup g){
AnimalFarm res = new AnimalFarm();
foreach(Animal a in this)
if (a.Group == g && a.Sex == Sex.Male) res.Add(a);
return res;
}
} | |||
|
Notice the way we implement the rejection in RemoveItem and ClearItems: We do not call the superclass operation.
In Program 45.7 (only on web) we show an AnimalFarm client program similar (but not not identical) to Program 45.4. The program output in Listing 45.8 (only on web) reveals the special semantics of the virtual, protected operations from Collection<T> - as redefined in Program 45.6.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | using System;
using System.Collections.ObjectModel;
class App{
public static void Main(){
AnimalFarm af = new AnimalFarm();
// Populating the farm with Add
af.Add(new Animal("elephant"));
af.Add(new Animal("giraffe"));
af.Add(new Animal("tiger"));
ReportList("Adding elephant, giraffe, and tiger with Add(...)", af);
// Additional population with Insert
af.Insert(0, new Animal("blueJay", AnimalGroup.Bird));
af.Insert(0, new Animal("goldenEagle", AnimalGroup.Bird));
ReportList("Inserting blue jay and golden eagle at index 0 with Insert(0, ...)", af);
// Extract birds:
AnimalFarm birds = af.GetGroup(AnimalGroup.Bird);
ReportList("The birds in farm - extraced with GetGroup", birds);
// Remove tiger
af.Remove(new Animal("tiger"));
ReportList("Removing tiger with Remove(...)", af);
// Remove animal at index 2
af.RemoveAt(2);
ReportList("Removing animal at index 2, with RemoveAt(2)", af);
// Clear the farm
af.Clear();
ReportList("Clear the farm with Clear()", af);
}
public static void ReportList<T>(string explanation, Collection<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.WriteLine("{0, 3}", el);
Console.WriteLine(); Console.WriteLine();
}
} | |||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 | Adding elephant, giraffe, and tiger with Add(...) Animal: elephant(Female) Animal: elephant(Male) Animal: giraffe(Female) Animal: giraffe(Male) Animal: tiger(Female) Animal: tiger(Male) Inserting blue jay and golden eagle at index 0 with Insert(0, ...) Animal: goldenEagle(Female) Animal: goldenEagle(Male) Animal: blueJay(Female) Animal: blueJay(Male) Animal: elephant(Female) Animal: elephant(Male) Animal: giraffe(Female) Animal: giraffe(Male) Animal: tiger(Female) Animal: tiger(Male) The birds in farm - extraced with GetGroup Animal: goldenEagle(Female) Animal: goldenEagle(Male) Animal: blueJay(Female) Animal: blueJay(Male) [Removal denied] Removing tiger with Remove(...) Animal: goldenEagle(Female) Animal: goldenEagle(Male) Animal: blueJay(Female) Animal: blueJay(Male) Animal: elephant(Female) Animal: elephant(Male) Animal: giraffe(Female) Animal: giraffe(Male) Animal: tiger(Female) Animal: tiger(Male) [Removal denied] Removing animal at index 2, with RemoveAt(2) Animal: goldenEagle(Female) Animal: goldenEagle(Male) Animal: blueJay(Female) Animal: blueJay(Male) Animal: elephant(Female) Animal: elephant(Male) Animal: giraffe(Female) Animal: giraffe(Male) Animal: tiger(Female) Animal: tiger(Male) [Clearing denied] Clear the farm with Clear() Animal: goldenEagle(Female) Animal: goldenEagle(Male) Animal: blueJay(Female) Animal: blueJay(Male) Animal: elephant(Female) Animal: elephant(Male) Animal: giraffe(Female) Animal: giraffe(Male) Animal: tiger(Female) Animal: tiger(Male) | |||
|
45.9. Overview of the class List<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We are now going to study the generic class List<T>. As it appears from Figure 45.1 both List<T> and Collection<T> implement the same interface, namely IList<T>, see Section 45.4. But as already noticed, List<T> offers many more operations than Collection<T>.
In the same style as in earlier sections, we provide an overview of the important operations of List<T>.
|
Compared with Collection<T> the class List<T> offers sorting, searching, reversing, and conversion operations. List<T> also has a number of "range operations" which operate on a number of elements via a single operation. We also notice a number of higher-order operations: Operations that take a delegate value (a function) as parameter. ConvertAll is a generic method which is parameterized with the type TOutput. ConvertAll accepts a function of delegate type which converts from type T to TOutput.
45.10. Sample use of class List<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this and the following sections we will show how to use some of the operations in List<T>. We start with a basic example similar to Program 45.1 in which we work on a list of characters: List<char>. We insert a number of char values into a list, and we remove some values as well. The program appears in Program 45.9 and the self-explaining output can be seen in Listing 45.10 (only on web). Notice in particular how the range operations InsertRange (line 28) and RemoveRange (line 40) operate on the list.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | using System;
using System.Collections.Generic;
/* Very similar to our illustration of class Collection<char> */
class BasicListDemo{
public static void Main(){
// List initialization and adding elements to the end of the list:
List<char> lst = new List<char>{'a', 'b', 'c'};
lst.Add('d'); lst.Add('e');
ReportList("Initial list, followed by lst.Add('d'); lst.Add('e');", lst);
// Mutate existing elements in the list
lst[0] = 'z'; lst[1]++;
ReportList("lst[0] = 'z'; lst[1]++;", lst);
// Insert and push towards the end
lst.Insert(0,'n');
ReportList("lst.Insert(0,'n');", lst);
// Insert at end - with Insert
lst.Insert(lst.Count,'x'); // equivalent to lst.Add('x');
ReportList("lst.Insert(lst.Count,'x');", lst);
// Insert a new list into existing list, at position 2.
lst.InsertRange(2, new List<char>{'1', '2', '3', '4'});
ReportList("lst.InsertRange(2, new List<char>{'1', '2', '3', '4'});", lst);
// Remove element 0 and push toward the beginning
lst.RemoveAt(0);
ReportList("lst.RemoveAt(0);", lst);
// Remove first occurrence of 'c'
lst.Remove('c');
ReportList("lst.Remove('c');", lst);
// Remove 2 elements, starting at element 1
lst.RemoveRange(1, 2);
ReportList("lst.RemoveRange(1, 2);", lst);
// Remove all remaining digits
lst.RemoveAll(delegate(char ch){return Char.IsDigit(ch);});
ReportList("lst.RemoveAll(delegate(char ch){return Char.IsDigit(ch);});", lst);
// Test of all remaining characters are letters
if (lst.TrueForAll(delegate(char ch){return Char.IsLetter(ch);}))
Console.WriteLine("All characters in lst are letters");
else
Console.WriteLine("NOT All characters in lst are letters");
}
public static void ReportList<T>(string explanation, List<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.Write("{0, 3}", el);
Console.WriteLine(); Console.WriteLine();
}
} | |||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | Initial list, followed by lst.Add('d'); lst.Add('e');
a b c d e
lst[0] = 'z'; lst[1]++;
z c c d e
lst.Insert(0,'n');
n z c c d e
lst.Insert(lst.Count,'x');
n z c c d e x
lst.InsertRange(2, new List<char>{'1', '2', '3', '4'});
n z 1 2 3 4 c c d e x
lst.RemoveAt(0);
z 1 2 3 4 c c d e x
lst.Remove('c');
z 1 2 3 4 c d e x
lst.RemoveRange(1, 2);
z 3 4 c d e x
lst.RemoveAll(delegate(char ch){return Char.IsDigit(ch);});
z c d e x
All characters in lst are letters | |||
|
45.11. Sample use of the Find operations in List<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this section we will illustrate how to use the search operations in List<T>. More specifically, we will apply the methods Find, FindAll and IndexOf on an instance of List<Point>, where Point is a type, such as defined by the struct in Program 14.12. The operations discussed in this section do all use linear search. It means that they work by looking at one element after the other, in a rather trivial way. As a contrast, we will look at binary search operations in Section 45.13, which searches in a "more advanced" way.
In the program below - Program 45.11 - we declare a List<Point> in line 11, and we add six points to the list in line 13-16. In line 20 we shown how to use Find to locate the first point in the list whose x-coordinate is equal to 5. The same is shown in line 25. The difference between the two uses of Find is that the first relies on a delegate given on the fly: delegate(Point q){return (q.Getx() == 5);}, while the other relies on an existing static method FindX5 (defined in line 40 - 42). The approach shown in line 20 is, in my opinion, superior.
In line 29 we show how to use the variant FindAll, which returns a Point list instead of just a single Point, as returned by Find. In line 36 we show how IndexOf can be used to find the index of a given Point in a Point list. It is worth asking how the Point parameter of IndexOf is compared with the points in Point list. The documentation states that the points are compared by use of the default equality comparer of the type T, which in our case is struct Point. We have discussed the default equality comparer in Section 42.9 in the slipstream of our coverage of the generic interfaces IEquatable<T> and IEqualityComparer<T>.
We use the static method ReportList to show a Point list on standard output. We call ReportList several times in Program 45.11. The program output is shown in Listing 45.12.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | using System;
using System.Collections.Generic;
class C{
public static void Main(){
System.Threading.Thread.CurrentThread.CurrentCulture =
new System.Globalization.CultureInfo("en-US");
List<Point> pointLst = new List<Point>();
// Construct points and point list:
pointLst.Add(new Point(0,0)); pointLst.Add(new Point(5, 9));
pointLst.Add(new Point(5,4)); pointLst.Add(new Point(7.1,-13));
pointLst.Add(new Point(5,-2)); pointLst.Add(new Point(14,-3.4));
ReportList("Initial point list", pointLst);
// Find first point in list with x coordinate 5
Point p = pointLst.Find(delegate(Point q){return (q.Getx() == 5);});
Console.WriteLine("Found with delegate predicate: {0}\n", p);
// Equivalent. Use predicate which is a static method
p = pointLst.Find(new Predicate<Point>(FindX5));
Console.WriteLine("Found with static member predicate: {0}\n", p);
// Find all points in list with x coordinate 5
List<Point> resLst = new List<Point>();
resLst = pointLst.FindAll(delegate(Point q){return (q.Getx() == 5);});
ReportList("All points with x coordinate 5", resLst);
// Find index of a given point in pointLst.
// Notice that Point happens to be a struct - thus value comparison
Point searchPoint = new Point(5,4);
Console.WriteLine("Index of {0} {1}", searchPoint,
pointLst.IndexOf(searchPoint));
}
public static bool FindX5(Point p){
return p.Getx() == 5;
}
public static void ReportList<T>(string explanation,List<T> list){
Console.WriteLine(explanation);
int cnt = 0;
foreach(T el in list){
Console.Write("{0, 3}", el);
cnt++;
if (cnt%4 == 0) Console.WriteLine();
}
if (cnt%4 != 0) Console.WriteLine();
Console.WriteLine();
}
} | |||
|
1 2 3 4 5 6 7 8 9 10 11 12 | Initial point list Point:(0,0). Point:(5,9). Point:(5,4). Point:(7.1,-13). Point:(5,-2). Point:(14,-3.4). Found with delegate predicate: Point:(5,9). Found with static member predicate: Point:(5,9). All points with x coordinate 5 Point:(5,9). Point:(5,4). Point:(5,-2). Index of Point:(5,4). 2 | |||
|
45.12. Sample use of Sort in List<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
As a client user of the generic class List<T> it is likely that you never need to write a sorting procedure! You are supposed to use one of the already existing Sort methods in List<T>.
Sorting the elements in a collection of elements of type T depends on a less than or equal operation on T. If the type T is taken directly from the C# libraries, it may very well be the case that we can just use the default less than or equal operation of the type T. If T is one of our own types, we will have to supply an implementation of the comparison operation ourselves. This can be done by passing a delegate object to the Sort method.
Below, in Program 45.13 we illustrate most of the four overloaded Sort operations in List<T>. The actual type parameter in the example, passed for T, is int. The program output (the lists before and after sorting) is shown in Listing 45.14 (only on web).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 | using System;
using System.Collections.Generic;
class C{
public static void Main(){
List<int> listOriginal = new List<int>{5, 3, 2, 7, -4, 0},
list;
// Sorting by means of the default comparer of int:
list = new List<int>(listOriginal);
ReportList(list);
list.Sort();
ReportList(list);
Console.WriteLine();
// Equivalent - explicit notatation of the Comparer:
list = new List<int>(listOriginal);
ReportList(list);
list.Sort(Comparer<int>.Default);
ReportList(list);
Console.WriteLine();
// Equivalent - explicit instantiation of an IntComparer:
list = new List<int>(listOriginal);
ReportList(list);
list.Sort(new IntComparer());
ReportList(list);
Console.WriteLine();
// Similar - use of a delegate value for comparison:
list = new List<int>(listOriginal);
ReportList(list);
list.Sort(delegate(int x, int y){
if (x < y)
return -1;
else if (x == y)
return 0;
else return 1;});
ReportList(list);
Console.WriteLine();
}
public static void ReportList<T>(List<T> list){
foreach(T el in list)
Console.Write("{0, 3}", el);
Console.WriteLine();
}
}
public class IntComparer: Comparer<int>{
public override int Compare(int x, int y){
if (x < y)
return -1;
else if (x == y)
return 0;
else return 1;
}
} | |||
|
Throughout Program 45.13 we do several sortings of listOriginal, as declared in line 8. In line 14 we rely the default comparer of type int. The default comparer is explained in the following way in the .NET framework documentation of List.Sort:
This method uses the default comparer Comparer<T>.Default for type T to determine the order of list elements. The Comparer<T>.Default property checks whether type T implements the IComparable generic interface and uses that implementation, if available. If not, Comparer<T>.Default checks whether type T implements the IComparable interface. If type T does not implement either interface, Comparer<T>.Default throws an InvalidOperationException.
The sorting done in line 21 is equivalent to line 14. In line 21 we show how to pass the default comparer of type int explicitly to the Sort method.
Let us now assume the type int does not have a default comparer. In other words, we will have to implement the comparer ourselves. The call of Sort in line 28 passes a new IntComparer instance to Sort. The class IntComparer is programmed in line 53-61, at the bottom of Program 45.13. Notice that IntComparer is a subclass of Comparer<int>, which is an abstract class in the namespace System.Collections.Generic with an abstract method named Compare. The generic class Comparer<T> is in many ways similar to the class EqualityComparer<T>, which we touched on in Section 42.9. Most important, both have a static Default property, which returns a comparer object.
As a final resort that always works we can pass a comparer function to Sort. In C#, such a function is programmed as a delegate. (Delegates are discussed in Chapter 22). Line 35-40 shows how this can be done. Notice that the delegate we use is programmed on the fly. This style of programming is a reminiscence of functional programming.
I find it much more natural to pass an ordering method instead of an object of a class with an ordering method. (The latter is a left over from older object-oriented programming languages in which the only way to pass a function F as parameter is via an object of a class in which F is an instance method). In general, I also prefer to be explicit about the ordering instead of relying on some default ordering which may turn out to surprise you.
1 2 3 4 5 6 7 8 9 10 11 | 5 3 2 7 -4 0 -4 0 2 3 5 7 5 3 2 7 -4 0 -4 0 2 3 5 7 5 3 2 7 -4 0 -4 0 2 3 5 7 5 3 2 7 -4 0 -4 0 2 3 5 7 | |||
|
Let us summarize the lessons that we have learned from the example:
|
| Exercise 12.1. Shuffle List Write a Shuffle operation that disorders the elements of a collection in a random fashion. A shuffle operation is useful in many context. There is no Shuffle operation in System.Collections.Generic.List<T>. In the similar Java libraries there is a shuffle method. In which class do you want to place the Shuffle operation? You may consider to make use of extension methods. You can decide on programming either a mutating or a non-mutating variant of the operation. Be sure to understand the difference between these two options. Test the operation on List<Card>. The class Card (representing a playing card) is one of the classes we have seen earlier in the course. Solution |
| Exercise 12.2. Course and Project classes In the earlier exercise about courses and projects (found in the lecture about abstract classes and interfaces) we refined the program about BooleanCourse, GradedCourse, and Project to use a common superclass called Course. Revise your solution (or the model solution) such that the courses in the class Project are represented as a variable of type List<Course> instead of by use of four variables of type Course. Reimplement and simplify the method Passed in class Project. Take advantage of the new representation of the courses in a project, such that the "3 out of 4 rule" (see the original exercise) is implemented in a more natural way. Solution |
45.13. Sample use of BinarySearch in List<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
The search operations discussed in Section 45.11 all implemented linear search processes. The search operations of this section implement binary search processes, which are much faster when applied on large collections. On collections of size n, linear search has - not surprisingly - time complexity O(n). Binary search has time complexity O(log n). When n is large, the difference between n and log n is dramatic.
The BinarySearch operations in List<T> require, as a precondition, that the list is ordered before the search is performed. If necessary, the Sort operation (see Section 45.12) can be used to establish the ordering.
You may ask why we should search for an element which we - in the starting point - is able to pass as input to the BinarySearch method. There is a couple of good answers. First, we may be interested to know if the element is present or not in the list. Second, it may also be possible to search for an incomplete object (by only comparing some selected fields in the Comparer method). Using this approach we are actually interested in finding the complete object, with all the data fields, in the collection.
If the BinarySearch operation finds an element in the list, the index of the element is returned. This is a non-negative integer. If the element is not found, a negative integer, say i, is returned. Below we will see that that -i (or more precisely the bitwise complement ~i) in that case is the position of the element, if it had been present in the list.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 | using System;
using System.Collections.Generic;
class BinarySearchDemo{
public static void Main(){
System.Threading.Thread.CurrentThread.CurrentCulture =
new System.Globalization.CultureInfo("en-US");
List<Point> pointLst = new List<Point>(); // Point is a struct.
// Construct points and point list:
pointLst.Add(new Point(0,0)); pointLst.Add(new Point(5, 9));
pointLst.Add(new Point(5,4)); pointLst.Add(new Point(7.1,-13));
pointLst.Add(new Point(5,-2)); pointLst.Add(new Point(14,-3.4));
ReportList("The initial point list", pointLst);
// Sort point list, using a specific point Comparer.
// Notice the PointComparer:
// Ordering according to sum of x and y coordinates
IComparer<Point> pointComparer = new PointComparer();
pointLst.Sort(pointComparer);
ReportList("The sorted point list", pointLst);
int res;
Point searchPoint;
// Run-time error.
// Failed to compare two elements in the array.
// searchPoint = new Point(5,4);
// res = pointLst.BinarySearch(searchPoint);
// Console.WriteLine("BinarySearch for {0}: {1}", searchPoint, res);
searchPoint = new Point(5,4);
res = pointLst.BinarySearch(searchPoint, pointComparer);
Console.WriteLine("BinarySearch for {0}: {1}", searchPoint, res);
searchPoint = new Point(1,8);
res = pointLst.BinarySearch(searchPoint, pointComparer);
Console.WriteLine("BinarySearch for {0}: {1}", searchPoint, res);
}
public static void ReportList<T>(string explanation,List<T> list){
Console.WriteLine(explanation);
int cnt = 0;
foreach(T el in list){
Console.Write("{0, 3}", el);
cnt++;
if (cnt%4 == 0) Console.WriteLine();
}
if (cnt%4 != 0) Console.WriteLine();
Console.WriteLine();
}
}
// Compare the sum of the x and y coordinates.
// Somewhat non-traditional!
public class PointComparer: Comparer<Point>{
public override int Compare(Point p1, Point p2){
double p1Sum = p1.Getx() + p1.Gety();
double p2Sum = p2.Getx() + p2.Gety();
if (p1Sum < p2Sum)
return -1;
else if (p1Sum == p2Sum)
return 0;
else return 1;
}
} | |||
|
Program 45.15 works on a list of points. Six points are created and inserted into a list in line 13-16. Next, in line 23, the list is sorted. As it appears from the Point comparer programmed in line 62-72, a point p is less than or equal to point q, if p.x + p.y <= q.x + q.y. You may think that this is odd, but it is our decision for this particular program example.
In line 33 we attempt to activate binary searching by use of the default comparer. But such a comparer does not exist for class Point. This problem is revealed at run-time.
In line 37 and 41 we search for the points (5,4) and (1,8) respectively. In both cases we expect to find the point (5,4), which happens to be located at place 3 in the sorted list. The output of the program, shown in Program 45.17 (only on web) confirms this.
1 2 3 4 5 6 7 8 9 10 | The initial point list Point:(0,0). Point:(5,9). Point:(5,4). Point:(7.1,-13). Point:(5,-2). Point:(14,-3.4). The sorted point list Point:(7.1,-13). Point:(0,0). Point:(5,-2). Point:(5,4). Point:(14,-3.4). Point:(5,9). BinarySearch for Point:(5,4). : 3 BinarySearch for Point:(1,8). : 3 | |||
|
In the next program, Program 45.17 we illustrate what happens if we search for a non-existing point with BinarySearch. The class PointComparer and the generic method ReportList are not shown in the paper version of Program 45.17. Please consult Program 45.15 where they both appear.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | using System;
using System.Collections.Generic;
class BinarySearchDemo{
public static void Main(){
System.Threading.Thread.CurrentThread.CurrentCulture =
new System.Globalization.CultureInfo("en-US");
List<Point> pointLst = new List<Point>();
// Construct points and point list:
pointLst.Add(new Point(0,0)); pointLst.Add(new Point(5, 9));
pointLst.Add(new Point(5,4)); pointLst.Add(new Point(7.1,-13));
pointLst.Add(new Point(5,-2)); pointLst.Add(new Point(14,-3.4));
ReportList("Initial point list", pointLst);
// Sort point list, using a specific point Comparer:
IComparer<Point> pointComparer = new PointComparer();
pointLst.Sort(pointComparer);
ReportList("Sorted point list", pointLst);
int res;
Point searchPoint;
searchPoint = new Point(1,1);
res = pointLst.BinarySearch(searchPoint, pointComparer);
Console.WriteLine("BinarySearch for {0}: {1}\n", searchPoint, res);
if (res < 0){ // search point not found
pointLst.Insert(~res, searchPoint); // Insert searchPoint such
// that pointLst remains sorted
Console.WriteLine("Inserting {0} at index {1}", searchPoint, ~res);
ReportList("Point list after insertion", pointLst);
}
}
public static void ReportList<T>(string explanation,List<T> list){
Console.WriteLine(explanation);
int cnt = 0;
foreach(T el in list){
Console.Write("{0, 3}", el);
cnt++;
if (cnt%4 == 0) Console.WriteLine();
}
if (cnt%4 != 0) Console.WriteLine();
Console.WriteLine();
}
}
// Compare the sum of the x and y coordinates.
// Somewhat non-traditional!
public class PointComparer: Comparer<Point>{
public override int Compare(Point p1, Point p2){
double p1Sum = p1.Getx() + p1.Gety();
double p2Sum = p2.Getx() + p2.Gety();
if (p1Sum < p2Sum)
return -1;
else if (p1Sum == p2Sum)
return 0;
else return 1;
}
} | |||
|
The scene of Program 45.17 is the same as that of Program 45.15. In line 28 we do binary searching, looking for the point (1,1). None of the points in the program have an "x plus y sum" of 2. Therefore, the point (1,1) is not located by BinarySearch. The BinarySearch method returns a negative ghost index. The ghost index is the bitwise complement of the index where to insert the point in such a way that the list will remain sorted. (Notice the bitwise complement operation ~ which turns 0 to 1 and 1 to 0 at the binary level). The program output reveals that position ~(-3) is the natural place of the point (1,1) to maintain the ordering of the list. Notice that the value of ~(-3) is 2, due the use of two's complement arithmetic. This explains the rationale of the negative values returned by BinarySearch.
The output of Program 45.17 is shown in Listing 45.18 (only on web).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | Initial point list Point:(0,0). Point:(5,9). Point:(5,4). Point:(7.1,-13). Point:(5,-2). Point:(14,-3.4). Sorted point list Point:(7.1,-13). Point:(0,0). Point:(5,-2). Point:(5,4). Point:(14,-3.4). Point:(5,9). BinarySearch for Point:(1,1). : -3 Inserting Point:(1,1). at index 2 Point list after insertion Point:(7.1,-13). Point:(0,0). Point:(1,1). Point:(5,-2). Point:(5,4). Point:(14,-3.4). Point:(5,9). | |||
|
Contrary to Sort, it is not possible to pass a delegate to BinarySearch. This seems to be a flaw in the design of the List<T> library.
We have learned the following lessons about BinarySearch:
|
45.14. Overview of the class LinkedList<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
The collections implemented by Collection<T> of Section 45.5 and List<T> of Section 45.9 were based on arrays. We will now turn our interest towards a list type, which is based on a linked representation.
Below, in Figure 45.2 we show the object-structure of a double linked list.

| Figure 45.2 A double linked list where instances of LinkedListNode keep the list together |
The generic class LinkedList<T> relies on a "building block class" LinkedListNode<T>. We need to deal with instances of LinkedListNodes when we work with linked lists in C#. In other words, LinkedListNode is not just a class behind the scene - it is an important class for clients of LinkedListNode<T>. In Figure 45.2 the five rectangular nodes are instances of LinkedListNode<T> for some element type T. The circular, green nodes are instances of the element type T. We will study LinkedListNode<T> in Section 45.15 after we have surveyed the list operations in LinkedList<T>.
As it can be seen from the class diagram of the list class in Figure 45.1, LinkedList<T> implements the interface ICollection<T>, see Section 45.3. Unlike Collection<T> and List<T>, LinkedList<T> does not implement indexed access, as of Ilist<T>. This is a natural choice because indexed access is not efficient in a linked representation. The following operations are available in LinkedList<T>:
|
A linked list can be constructed as an empty collection or as a collection filled with elements from another collection, represented as an IEnumerable<T>, see Section 45.2.
The First and Last properties access the first/last LinkedListNode in the double linked list. Count returns the number of elements in the list - not by counting them each time Count is referred - but via some bookkeeping information encapsulated in a linked list object. Thus, Count is an O(1) operation.
Although LinkedList<T> implements the generic interface ICollection<T>, which has a method named Add, the Add operation is not readily available on linked lists. We will in Program 45.19 show that Add is present as an explicit interface implementation, see Section 31.8. Instead of Add, the designers of LinkedList<T> want us to use one of the AddRelative operations: AddFirst, AddLast, AddBefore, and AddAfter. None of these are prescribed by the interface ICollection<T>, however. Each of the AddRelative operations are overloaded in two variants, such that we can add an element of type T or an object of type LinkedListNode<T> (which in turn reference an object of type T).
Using the Remove methods, it is possible to remove an element of type T or a specific instance of LinkedListNode<T>. Remove(T) is an O(n) operation; Remove(LinkedListNode<T>) is an O(1) operation. There are also parameter-less methods for removing the first/last element in the linked list. The time complexity of these are O(1).
Finally there are linear search operations from either end of the list: Find and FindLast. The boolean Contains operation is similar to the Find operations. These operations all seem to rely on the Equals operation inherited from class Object. In that way Find, FindLast and Contains are more primitive (not as well-designed) as the similar methods in List<T>. (The documentation in the .NET libraries is silent about these details).
45.15. The class LinkedListNode<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
As illustrated in Figure 45.2, instances of the generic class LinkedListNode<T> keep a linked list together. In the figure, the rectangular boxes are instances of LinkedListNode<T>. From the figure it appears that each instance of LinkedListNode<T> has three references: One to the left, one to the element, and one to the right. Actually, there is a fourth reference, namely to the linked list instance to which a given LinkedListNode object belongs.
The class LinkedListNode<T> is sealed, generic class that represents a non-mutable node in a linked list A LinkedListNode can at most belong to a single linked list |
The members of LinkedListNode<T> are as follows:
|
The properties Next and Previous access neighbor instances of LinkedListNode<T>. Value accesses the element of type T. List accesses the linked list to which the instance of LinkedListNode belongs. Next, Previous, and List are all getters. Value is both a getter and a setter.
It is not possible to initialize or to mutate the fields behind the properties Next, Previous, and List via public interfaces. It is clearly the intention that the linked list - and only linked list - has authority to change these fields. If we programmed our own, special-purpose linked list class it would therefore not be easy to reuse the class LinkedListNode<T>. This is unfortunate.
Related to the discussion about the interface of LinkedListNode<T> we may ask how LinkedList is allowed to access the private/internal details of an instance of LinkedListNode. The best guess seems to be that the fields are internal.
45.16. Sample use of class LinkedList<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We will illustrate the use of LinkedList<T> and LinkedListNode<T> in Program 45.19. In line 8 we make a linked list of integers from an array. Notice the use of the LinkedList constructor LinkedList(IEnumerable<T>).
In line 16 we attempt to add the integer 17 to the linked list. This is not possible, because the method Add is not easily available, see the discussion in Section 45.14. If we insist to use Add, it must be done as in line 20. Most likely, you should use one of the Add variants instead, for instance AddFirst or AddLast.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | using System;
using System.Collections.Generic;
class LinkedListDemo{
public static void Main(){
LinkedList<int> lst = new LinkedList<int>(
new int[]{5, 3, 2, 7, -4, 0});
ReportList("Initial LinkedList", lst);
// Using Add.
// Compile-time error: 'LinkedList<int>' does not contain a
// definition for 'Add'
// lst.Add(17);
// ReportList("lst.Add(17);" lst);
// Add is implemented as an explicit interface implementation
((ICollection<int>)lst).Add(17);
ReportList("((ICollection<int>)lst).Add(17);", lst);
// Using AddFirst and AddLast
lst.AddFirst(-88);
lst.AddLast(88);
ReportList("lst.AddFirst(-88); lst.AddFirst(88);", lst);
// Using Remove.
lst.Remove(17);
ReportList("lst.Remove(17);", lst);
// Using RemoveFirst and RemoveLast
lst.RemoveFirst(); lst.RemoveLast();
ReportList("lst.RemoveFirst(); lst.RemoveLast();", lst);
// Using Clear
lst.Clear();
ReportList("lst.Clear();", lst);
}
public static void ReportList<T>(string explanation, LinkedList<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.Write("{0, 4}", el);
Console.WriteLine(); Console.WriteLine();
}
} | |||
|
The output of Program 45.19 is shown in Listing 45.20. By studying Listing 45.20 you will learn additional details of the LinkedList operations.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | Initial LinkedList 5 3 2 7 -4 0 ((ICollection<int>)lst).Add(17); 5 3 2 7 -4 0 17 lst.AddFirst(-88); lst.AddFirst(88); -88 5 3 2 7 -4 0 17 88 lst.Remove(17); -88 5 3 2 7 -4 0 88 lst.RemoveFirst(); lst.RemoveLast(); 5 3 2 7 -4 0 lst.Clear(); | |||
|
The LinkedList example in Program 45.19 did not show how to use LinkedListNodes together with LinkedList<T>. To make up for that we will in Program 45.21 concentrate on the use of LinkedList<T> and LinkedListNode<T> together.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | using System;
using System.Collections.Generic;
class LinkedListNodeDemo{
public static void Main(){
LinkedList<int> lst = new LinkedList<int>(
new int[]{5, 3, 2, 7, -4, 0});
ReportList("Initial LinkedList", lst);
LinkedListNode<int> node1, node2, node;
node1 = lst.First;
node2 = lst.Last;
// Run-time error.
// The LinkedListNode is already in the list.
// Error message: The LinkedList node belongs a LinkedList.
/* lst.AddLast(node1); */
// Move first node to last node in list
lst.Remove(node1); lst.AddLast(node1);
ReportList("node1 = lst.First; lst.Remove(node1); lst.AddLast(node1);", lst);
// Navigate in list via LinkedListNode objects
node1 = lst.First;
Console.WriteLine("Third element in list: node1 = lst.First; node1.Next.Next.Value == {0}\n",
node1.Next.Next.Value);
// Add an integer after a LinkedListNode object
lst.AddAfter(node1, 17);
ReportList("lst.AddAfter(node1, 17);", lst);
// Add a LinkedListNode object after another LinkedListNode object
lst.AddAfter(node1, new LinkedListNode<int>(18));
ReportList("lst.AddAfter(node1, new LinkedListNode<int>(18));" , lst);
// Navigate in LinkedListNode objects and add an int before a node:
node = node1.Next.Next.Next;
lst.AddBefore(node, 99);
ReportList("node = node1.Next.Next.Next; lst.AddBefore(node, 99); " , lst);
// Navigate in LinkedListNode objects and remove a node.
node = node.Previous;
lst.Remove(node);
ReportList("node = node.Previous; lst.Remove(node);" , lst);
}
public static void ReportList<T>(string explanation, LinkedList<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.Write("{0, 4}", el);
Console.WriteLine(); Console.WriteLine();
}
} | |||
|
In line 8-9 we make the same initial integer list as in Program 45.19. In line 13-14 we see how to access to the first/last LinkedListNode objects of the list.
In line 19 we attempt to add node1, which is the first LinkedListNode in lst, as the last node of the list. This fails because it could bring the linked list into an inconsistent state. (Recall in this context that a LinkedListNode knows the list to which it belongs). Instead, as shown in line 22, we should first remove node1 and then add node1 with AddLast.
Please take a close look at the remaining addings, navigations, and removals in Program 45.21. As above, we show a self-explaining output of the program, see Listing 45.22.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | Initial LinkedList 5 3 2 7 -4 0 node1 = lst.First; lst.Remove(node1); lst.AddLast(node1); 3 2 7 -4 0 5 Third element in list: node1 = lst.First; node1.Next.Next.Value == 7 lst.AddAfter(node1, 17); 3 17 2 7 -4 0 5 lst.AddAfter(node1, new LinkedListNode<int>(18)); 3 18 17 2 7 -4 0 5 node = node1.Next.Next.Next; lst.AddBefore(node, 99); 3 18 17 99 2 7 -4 0 5 node = node.Previous; lst.Remove(node); 3 18 17 2 7 -4 0 5 | |||
|
45.17. Time complexity overview: Collection classes
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this section we will discuss the efficiency of selected and important list operations in the three classes Collection<T>, List<T>, and LinkedList<T>. This is done by listing the time complexities of the operations in a table, see Table 45.1. If you are not comfortable with Big O notation, you can for instance consult Wikipedia [Big-O] or a book about algorithms and data structures.
The time complexities of the list operations are most often supplied as part of the documentation of the operations. The choice of one list type in favor of another is often based on requirements to the time complexities of important operations. Therefore you should pay careful attention to the information about time complexities in the C# library documentation.
Throughout the discussion we will assume that the lists contain n elements. It may be helpful to relate the table with the class diagram in Figure 45.1 from which it appears which interfaces to expect from the list classes.
| Operation | Collection<T> | List<T> | LinkedList<T> |
| this[i] | O(1) | O(1) | - |
| Count | O(1) | O(1) | O(1) |
| Add(e) | O(1) or O(n) | O(1) or O(n) | O(1) |
| Insert(i,e) | O(n) | O(n) | - |
| Remove(e) | O(n) | O(n) | O(n) |
| IndexOf(e) | O(n) | O(n) | - |
| Contains(e) | O(n) | O(n) | O(n) |
| BinarySearch(e) | - | O(log n) | - |
| Sort() | - | O(n log n) or O(n2) | - |
| AddBefore(lln) | - | - | O(1) |
| AddAfter(lln,e) | - | - | O(1) |
| Remove(lln) | - | - | O(1) |
| RemoveFirst() | - | - | O(1) |
| RemoveLast() | - | - | O(1) |
| Table 45.1 Time complexities of important operations in the classes Collection<T>, List<T>, and LinkedList<T>. |
As it can be seen in the class diagram of Figure 45.1 all three classes implement the ICollection<T> interface with the operations Count, Add, Remove, and Contains. Thus, these four operations appear for all classes in Table 45.1.
Count is efficient for all lists, because it maintains an internal counter, the value of which can be returned by the Count property. Thus, independent of the length of a list, Count runs in constant time.
For all three types of lists, Add(e) adds an element e (of type T) to the end of the list. This can be done in constant time, because all the three types of lists have direct access the rear end of the list. The time complexity O(1)/O(n) given for Collection<T> and List<T> reflects that under normal circumstances it takes only constant time to add an element to a Collection or a List. If however, the list is full it may need resizing, and in that case the run time is linear in n.
Remove(e) and Contains(e), where e is of type T, will have to search for e in the list. This behavior is common for all three types of lists. Therefore the run times of Remove and Contains are O(n).
The indexer this[i] is only available in the lists that implement Ilist<T>. Such lists are based on arrays, and therefore the runtime of the indexer is O(1). (Recall that in arrays it is possible to compute the location of an element with a given index; No searching, whatsoever, is involved).
BinarySearch and Sort are operations in List<T>. Sort implements a Quicksort variant, and as such the worst possible time complexity is O(n2), but the expected time complexity is O(n log n). The runtime of BinarySearch is, as expected, O(log n).
The bottom five operations in the table belong to LinkedList. The methods AddBefore, AddAfter, and Remove all work on a LinkedListNode, lln, and as such their runtimes do not depend on n. (Only a few references need to be assigned. The number of pointer assignments do not depend on n). Thus, when applied on objects of type LinkedListNode the runtime of these three operations are O(1). RemoveFirst and RemoveLast are of time complexity O(1) because a linked list maintain direct references to both ends of the list.
45.18. Using Collections through Interfaces
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We started this chapter with a discussion of list interfaces, and we will end the chapter in a similar way.
It is, of course, necessary to use one of the collection classes (such as List<T>) when you need a collection in your program. The morale of this section is, however, that you should not use list classes more than necessary. In short, you should typically use List<T> or Collection<T> (for some type T) when you make a collection object. All other places you are better off using one of the interface types, such as IList<T>. The key observations can be summarized as follows.
It is an advantage to use collections via interfaces instead of classes If possible, only use collection classes in instantiations, just after new This leads to programs with fewer bindings to concrete implementations of collections With this approach, it is easy to replace a collection class with another |
Thus, please consider the following when you use collections:
Program against collection interfaces, not collection classes
If the types of variables and parameters are given as interfaces it is easy, a later point in time, to change the representation of your collections (say, from Collection<T> to one of your own collections which implements Ilist<T>). Notice that if you, for instance, apply List<T> operations, which are not prescribed by one of the interfaces, you need to declare your list of type List<T> for some type T.
Let us illustrate how this can be done in Program 45.23. The thing to notice is that the only place we refer to a list class (here Collection<Animal>() ) is in line 9: new Collection<Animal>. All other places, as emphasized with purple, we use the interface ICollection<Animal>. If we, tomorrow, wish to change the representation of the animal collection, the only place to modify is line 9.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | using System;
using System.Collections.Generic;
using System.Collections.ObjectModel;
class CollectionInterfaceDemo{
public static void Main(){
ICollection<Animal> lst = new Collection<Animal>();
// Add elements to the end of the empty list:
lst.Add(new Animal("Cat")); lst.Add(new Animal("Dog", Sex.Female));
lst.Add(new Animal("Mouse")); lst.Add(new Animal("Rat"));
lst.Add(new Animal("Mouse", Sex.Female)); lst.Add(new Animal("Rat"));
lst.Add(new Animal("Herring", AnimalGroup.Fish, Sex.Female));
lst.Add(new Animal("Eagle", AnimalGroup.Bird, Sex.Male));
// Report in various ways on the animal collection:
Print("Initial List", lst);
ReportFemaleMale(lst);
ReportGroup(lst);
}
public static void Print<T>(string explanation, ICollection<T> list){
Console.WriteLine(explanation);
foreach(T el in list)
Console.WriteLine("{0, 3}", el);
Console.WriteLine(); Console.WriteLine();
}
public static void ReportFemaleMale(ICollection<Animal> list){
int numberOfMales = 0,
numberOfFemales = 0;
foreach(Animal a in list)
if (a.Sex == Sex.Male) numberOfMales++;
else if (a.Sex == Sex.Female) numberOfFemales++;
Console.WriteLine("Males: {0}, Females: {1}",
numberOfMales, numberOfFemales);
}
public static void ReportGroup(ICollection<Animal> list){
int numberOfMammals = 0,
numberOfBirds = 0,
numberOfFish = 0;
foreach(Animal a in list)
if (a.Group == AnimalGroup.Mammal) numberOfMammals++;
else if (a.Group == AnimalGroup.Bird) numberOfBirds++;
else if (a.Group == AnimalGroup.Fish) numberOfFish++;
Console.WriteLine("Mammals: {0}, Birds: {1}, Fish: {2}",
numberOfMammals, numberOfBirds, numberOfFish);
}
} | |||
|
On the accompanying slide we show versions of Program 45.23, which are tightly bound to the class Collection<Animal>, and we show a version in which we have replaced Collection<Animal> with List<Animal>.
45.19. References
| [Big-O] | Wikipedia: Big O Notation http://en.wikipedia.org/wiki/Big_O_notation |