   | Generic Types and Methods |
| A complete PDF version of the text book is now available. The PDF version is an almost complete subset of the HTML version (where only a few, long program listings have been removed). See here. |
   | Generic Types and Methods |
| A complete PDF version of the text book is now available. The PDF version is an almost complete subset of the HTML version (where only a few, long program listings have been removed). See here. |
Generic types are types that carry type parameters. Type parameterized classes will be of particular importance. The motivation for working with type parameterized classes was gained in Chapter 41.
42.1. The generic class Set<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Let us, right away, present the generic set class Set<T>. It is shown in Program 42.1. As usual, we show an abbreviated version of the class in the paper edition of the material.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 | using System;
using System.Collections.Generic;
using System.Collections;
public class Set<T> {
private int capacity;
private static int DefaultCapacity = 10;
private T[] store;
private int next;
public Set(int capacity){
this.capacity = capacity;
store = new T[capacity];
next = 0;
}
public Set(): this(DefaultCapacity){
}
public Set(T[] elements): this(elements.Length){
foreach(T el in elements) this.Insert(el);
}
// Copy constructor
public Set(Set<T> s): this(s.capacity){
foreach(T el in s) this.Insert(el);
}
public bool Member(T element){
for(int idx = 0; idx < next; idx++)
if (element.Equals(store[idx]))
return true;
return false;
}
public void Insert(T element){
if (!this.Member(element)){
if (this.Full){
Console.WriteLine("[Resize to {0}]", capacity * 2);
Array.Resize<T>(ref store, capacity * 2);
capacity = capacity * 2;
}
store[next] = element;
next++;
}
}
public void Delete(T element){
bool found = false;
int foundIdx = 0;
for(int idx = 0; !found && (idx < next); idx++){
if (element.Equals(store[idx])){
found = true;
foundIdx = idx;
}
}
if (found){ // shift remaining elements left
for(int idx = foundIdx+1; idx < next; idx++)
store[idx-1] = store[idx];
store[next-1] = default(T);
next--;
}
}
public int Count{
get{
return next;
}
}
// Is this set a subset of other
public bool Subset(Set<T> other){
foreach(T e in this)
if (!other.Member(e))
return false;
return true;
}
public override string ToString(){
string elRes = "";
for(int idx = 0; idx < next; idx++)
elRes += " " + store[idx];
return "{" + elRes + " "+ "}";
}
private bool Full{
get{
return next == capacity;
}
}
public IEnumerator<T> GetEnumerator (){
return new SetEnumerator(this);
}
private class SetEnumerator: IEnumerator<T>{
private readonly Set<T> set;
private int idx;
public SetEnumerator (Set<T> s){
this.set = s;
idx = -1; // position enumerator outside range
}
public T Current{
get {
return set.store[idx];
}
}
Object IEnumerator.Current{
get {
return set.store[idx];
}
}
public bool MoveNext(){
if (idx < set.next - 1){
idx++;
return true;
}
else
return false;
}
public void Reset(){
idx = -1;
}
public void Dispose(){
}
}
} | |||
|
The advantage of class Set<T> over class ObjectSet becomes clear when we study a client of Set<T>. Please take a look at Program 42.2 and compare it with Program 41.10. We are able to work with both sets of value types, such as Set<int>, and sets of reference types, such as Set<Die>. When we take an element out of the set it is not necessary to cast it, as in Program 41.10. Notice that a foreach loop does not provide the best illustration of this aspect, because the type in foreach(type var in collection) is used implicitly for casting a value in collection to type. The only way to access elements in a set is to use its iterator. Please take a look at Exercise 11.2 if you wish to go deeper into this issue.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | using System;
using System.Collections;
class App{
public static void Main(){
Die d1 = new Die(6), d2 = new Die(10),
d3 = new Die(16), d4 = new Die(8);
int sum = 0;
string netString = "";
// Working with sets of dice:
Set<Die> s1 = new Set<Die>( // A set of dice
new Die[]{d1, d2, d3, d4});
foreach(Die d in s1){
d.Toss();
Console.WriteLine("{0}", d);
}
// Working with sets of ints
Set<int> s2 = new Set<int>( // A set of ints
new int[]{1, 2, 3, 4});
foreach(int i in s2)
sum += i;
Console.WriteLine("Sum: {0}", sum);
// Working with sets of strings
Set<string> s3 = new Set<string>( // A set of strings
new string[]{"a", "b", "c", "d"});
foreach(string str in s3)
netString += str;
Console.WriteLine("Appended string: {0}", netString);
}
} | |||
|
The output of Program 42.2 is shown in Listing 42.3 (only on web).
1 2 3 4 5 6 | Die[6]:3 Die[10]:10 Die[16]:16 Die[8]:8 Sum: 10 Appended string: abcd | |||
|
| Exercise 11.1. Intersection, union, and difference: Operations on sets On the accompanying slide we have shown a generic class set<T>. Add the classical set operations intersection, union and set difference to the generic class set<T>. Test the new operations from a client program. Hint: The enumerator, that comes with the class set<T>, may be useful for the implementation of the requested set operations. Solution |
| Exercise 11.2. An element access operation on sets The only way to get access to an element from a set is via use of the enumerator (also known as the iterator) of the set. In this exercise we wish to change that. Invent some operation on the set that allows you to take out an existing element in the set. This corresponds to accessing a given item in an array or a list, for instance via an indexer: arr[i] and lst[j]. Notice in this context that there is no order between elements in the set. It is not natural to talk about "the first" or "the last" element in the set. Given the invented operation in Set<T> use it to illustrate that, for some concrete type T, no casting is necessary when elements are accessed from Set<T> There is no solution to this exercise |
42.2. Generic Types
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Let us now describe the general concepts behind Generic Types in C#. C# supports not only generic classes, but also generic structs (see Section 42.7), generic interfaces (see Section 42.8), and generic delegate types (see Section 43.2 ). Overall, we distinguish between templates and constructed types:
|
When we talk about a generic type we do it in the meaning of a template.
The word "template" is appropriate, and in fact just to the point. But most C# writers do not use it, because the word "template" it used in C++ in a closely related, but slightly different meaning. A template in C++ is a type parameterized class, which is expanded at compile time. Each actual type parameter will create a new class, just like we would create it ourselves in a text editor. In C#, generic classes are able to share the class representation at run-time. For more details on these matters, consult for instance [Golding05].
As a possible coding style, it is often recommended to use capital, single letter names (such as S, T, and U) as formal type parameters. In that way it becomes easier to recognize templates, to spot formal type names in our programs, to keep templates apart from constructed types, and to avoid long and complicated name clauses of generic types. In situations where a type takes more than one formal type parameters, an alternative coding style calls for formal type parameter names like Tx and Ty, (such as TKey and TValue) where x and y describe the role of each of the formal type parameters.
The ability to have generic types is known as parametric polymorphism |
42.3. Constraints on Formal Type Parameters
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Let us again consider our implementation of the generic class Set<T> in Program 42.1. Take a close look at the class, and find out if we make any assumptions about the formal type parameter T in Program 42.1. Will any type T really apply? Please consider this, before you proceed!
In Set<T> it happens to be the case that we do not make any assumption of the type parameter T. This is typical for collection classes (which are classes that serve as element containers).
It is possible to express a number of constraints on a formal type parameter The more constraints on T, the more we can do on T-objects in the body of C<T> |
Sometimes we write a parameterized class, say C<T>, in which we wish to be able to make some concrete assumptions about the type parameter T. You may ask what we want to express. We could, for instance, want to express that
It turns out that the constraints in 1, 2, 6, 7, and 8 can be expressed directly in C#. The constraints in 4 and 5 can be expressed indirectly in C#, whereas the constraint in 3 cannot be expressed in C#.
Here follows a number of generic classes that illustrates the legal form of constraints. We define generic classes C, E, F, and G all of which are subclasses of class D. A and B are classes defined elsewhere. The constraints are colored in Program 42.4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | class C<S,T>: D
where T: A, ICloneable
where S: B {
...
}
class E<T>: D
where T: class{
...
}
class F<T>: D
where T: struct{
...
}
class G<T>: D
where T: new(){
...
} | |||
|
The class C has formal type parameters S and T. The first constraint requires that T is A, or a subclass of A, and that it implements the interface IClonable. Thus, only class A or subclasses of A that implement IClonable can be used as actual parameter corresponding to T. The type parameter S must be B or a subclass of B.
The class E has a formal type parameter T, which must be a class. In the same way, the class F has a formal type parameter T, which must be a struct.
The class G has a formal type parameter T, which must have a parameterless constructor.
As a consequence of the inheritance rules in C#, only a single class can be given in a constraint. Multiple interfaces can be given. A class should come before any interface. Thus, in line 2 of Program 42.4, A can be a class, and everything after A in the constraint need to be interfaces.
42.4. Constraints: Strings of comparable elements
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We will now program a generic class with constraints. We will make a class String<T> which generalizes System.String from C#. An instance of String<T> contains a sequence of T-values/ T-objects. In contrast, an instance of System.String contains a sequence of Unicode characters. With use of String<T> we can for instance make a string of integers, a string of bank accounts, and a string of dice.
Old-fashioned character strings can be ordered, because we have an ordering of characters. The ordering we have in mind is sometimes called lexicographic ordering, because it reflects the ordering of words in dictionaries and encyclopedia. We also wish to support ordering of our new generalized strings from String<T>. It can only be achieved if we provide an ordering of the values/objects in T. This is done by requiring that T implements the interface IComparable, which has a single method CompareTo. For details on IComparable and CompareTo, please consult Section 31.5.
Now take a look at the definition of String<T> in Program 42.5. In line 3 we state that String<T> should implement the interface IComparable<String<T>>. It is important to understand that we hereby commit ourselves to implement a CompareTo method in String<T>.
You may be confused about the interface IComparable, as discussed in Program 42.5 in contrast to IComparable<S>, which is used as IComparable<String<T>> in line 3 of Program 42.5. IComparable<S> is a generic interface. It is generic because this allows us to specify the parameter to the method CompareTo with better precision. We discuss the generic interface IComparable<S> in Section 42.8.
There is an additional important detail in line 3 of Program 42.5, namely the constraint, which is colored. The constraint states that the type T must be IComparable itself (again using the generic version of the interface). In plain English it means that there must be a CompareTo method available on the type, which we provide as the actual type parameter of our new string class. Our plan is, of course, to use the CompareTo method of T to program the CompareTo method of String<T>.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | using System;
public class String<T>: IComparable<String<T>> where T: IComparable<T>{
private T[] content;
public String(){
content = new T[0];
}
public String(T e){
content = new T[]{e};
}
public String(T e1, T e2){
content = new T[]{e1, e2};
}
public String(T e1, T e2, T e3){
content = new T[]{e1, e2, e3};
}
public int CompareTo(String<T> other){
int thisLength = this.content.Length,
otherLength = other.content.Length;
for (int i = 0; i < Math.Min(thisLength,otherLength); i++){
if (this.content[i].CompareTo(other.content[i]) < 0)
return -1;
else if (this.content[i].CompareTo(other.content[i]) > 0)
return 1;
}
// longest possible prefixes of this and other are pair-wise equal.
if (thisLength < otherLength)
return -1;
else if (thisLength > otherLength)
return 1;
else return 0;
}
public override string ToString(){
string res = "[";
for(int i = 0; i < content.Length;i++){
res += content[i];
if (i < content.Length - 1) res += ", ";
}
res += "]";
return res;
}
} | |||
|
In line 5 we see that a string of T-elements is represented as an array of T elements. This is a natural and straightforward choice. Next we see four constructors, which allows us to make strings of zero, one, two or three parameters. This is convenient, and good enough for toy usage. For real life use, we need a general constructor that accepts an array of T elements. The can most conveniently be made by use of parameter arrays, see Section 20.9.
After the constructors, from line 23-39, we see our implementation of CompareTo. From an overall point of view we can observe that it uses CompareTo of type T, as discussed above. This is the blue aspects in line 28 and 30. It may be sufficient to make this observation for some readers. If you want to understand what goes on inside the method, read on.
Recall that CompareTo must return a negative result if the current object is less than other, 0 if the current object is equal to other, and a positive result if the current object is greater than other. The for-loop in line 27 traverses the overlapping prefixes of two strings. Inside the loop we return a result, if it is possible to do so. If the for-loop terminates, the longest possible prefixes of the two string are equal to each other. The lengths of the two strings are now used to determine a result.
If T is the type char, if the current string is "abcxy", and if other is "abcxyz", we compare "abcxy" with "abcxy" in the for loop. "abcxy" is shorter than "abcxyz", and therefore the result of the comparison -1.
The method ToString starting in line 41 allows us to print instances of String<T> surrounded by square brackets [...]
In Program 42.6 we see a client class of String<T>. We construct and compare strings of integers, strings of strings, strings of doubles, strings of booleans, and strings of dice. The dimmed method ReportCompare activates the String<T> operation CompareTo on pairs of such strings. ReportCompare is a generic method, and it will be "undimmed" and explained in Program 43.1. Take a look at the program output in Listing 42.7 and be sure that you can understand the results.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | using System;
class StringApp{
public static void Main(){
ReportCompare(new String<int>(1, 2),
new String<int>(1));
ReportCompare(new String<string>("1", "2", "3"),
new String<string>("1"));
ReportCompare(new String<double>(0.5, 1.7, 3.0),
new String<double>(1.0, 1.7, 3.0));
ReportCompare(new String<bool>(true, false),
new String<bool>(false, true));
ReportCompare(new String<Die>(new Die(), new Die()),
new String<Die>(new Die(), new Die()));
}
public static void ReportCompare<T>(String<T> s, String<T> t)
where T: IComparable<T>{
Console.WriteLine("Result of comparing {0} and {1}: {2}",
s, t, s.CompareTo(t));
}
} | |||
|
1 2 3 4 5 | Result of comparing [1, 2] and [1]: 1 Result of comparing [1, 2, 3] and [1]: 1 Result of comparing [0,5, 1,7, 3] and [1, 1,7, 3]: -1 Result of comparing [True, False] and [False, True]: 1 Result of comparing [[3], [6]] and [[3], [5]]: 1 | |||
|
| Exercise 11.3. Comparable Pairs This exercise is inspired by an example in the book by Hansen and Sestoft: C# Precisely. Program a class ComparablePair<T,U> which implements the interface IComparable<ComparablePair<T,U>>. If you prefer, you can build the class ComparablePair<T,U> on top of class Pair<S,T> from an earlier exercise in this lecture. It is required that T and U are types that implement Icomparable<T> and Icomparable<U> respectively. How is that expressed in the class ComparablePair<T,U>? The generic class ComparablePair<T,U> should represent a pair (t,u) of values/objects where t is of type T and u is of type U. The generic class should have an appropriate constructor that initializes both parts of the pair. In addition, there should be properties that return each of the parts. Finally, the class should - of course - implement the operation CompareTo because it is prescribed by the interface System.IComparable<ComparablePair<T,U>>. Given two pairs p = (a,b) and q= (c,d). p is considered less than q if a is less than c. If a is equal to c then b and d controls the ordering. This is similar to lexicographic ordering on strings. If needed, you may get useful inspiration from the Icomparable class String<T> on the accompanying slide. Be sure to test-drive your solution! Solution |
42.5. Another example of constraints
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We will now illustrate the need for the class and struct constraints. We have already touched on these constraints in our discussion of Program 42.4.
In Program 42.8 we have two generic classes C and D. Each of them have a single type parameter, T and U respectively. As shown with red color in line 7 and 15, the compiler complains. In line 7 we assign the value null to the variable f of type T. In line 15 we make a nullable type U? from U. (If you wish to be reminded about nullable types, consult Section 14.9). Before you go on, attempt to explain the error messages, which are shown as comments in Program 42.8.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | /* Example from Hansen and Sestoft: C# Precisely */
class C<T>{
// Compiler Error message:
// Cannot convert null to type parameter 'T' because it could
// be a value type. Consider using 'default(T)' instead.
T f = null;
}
class D<U>{
// Compiler Error message:
// The type 'U' must be a non-nullable value type in order to use
// it as parameter 'T' in the generic type or method
// 'System.Nullable<T>'
U? f;
} | |||
|
In Program 42.9 we show new versions of C<T> and D<U>. Shown in purple we emphasize the constraints that are necessary for solving the problems.
The instance variable f of type T in C<T> is assigned to null. This only makes sense if T is a reference type. Therefore the class constraint on T is necessary.
The use of U? in D<U> only makes sense if U is a value type. (To understand this, you are referred to the discussion in Section 14.9). Value types in C# are provided by structs (see Section 6.6). The struct constraint on U is therefore the one to use.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | /* Example from Hansen and Sestoft: C# Precisely */
class C<T> where T: class{
T f = null;
}
class D<U> where U: struct{
U? f;
}
class Appl{
// Does NOT compile:
C<double> c = new C<double>();
D<A> d = new D<A>();
// OK:
C<A> c1 = new C<A>();
D<double> d1 = new D<double>();
}
class A{} | |||
|
In line 11-21 we show clients of C<T> and D<U>. The compiler errors in line 14 and 15 are easy to explain. The type double is not a reference type, and A, which is programmed in line 23, is not a value type. Therefore double and A violate the constraints of C<T> and D<U>. In line 18 and 19 we switch the roles of double and A. Now everything is fine.
42.6. Variance
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Consider the question asked in the following box.
A CheckAccount is a BankAccount But is a Set<CheckAccount> a Set<BankAccount> ? |
You are encouraged to review our discussion of the is a relation in Section 25.2.
The question is how Set<T> is varies when T varies. Variation in this context is specialization, cf. Chapter 25. Is Set<T> specialized when T is specialized?
Take a look at Program 42.10. In line 7-14 we construct a number of bank accounts and check accounts, and we make a set of bank accounts (s1, in line 17) and a set of check accounts (s2, in line 18). In line 21 and 22 we populate the two sets. So far so good. Next, in line 25 (shown in purple) we play the polymorphism game as we have done many times earlier, for example in line 13 of Program 28.17. If Set<CheckAccount> is a Set<BankAccount> line 25 of Program 42.10 should be OK (just as line 13 of Program 28.17 is OK).
The compiler does not like line 25, however. The reason is that Set<CheckAccount> is NOT a Set<BankAccount>.
If we for a moment assume that Set<CheckAccount> is a Set<BankAccount> the rest of the program reveals the troubles. We insert a new BankAccount object in s1, and via the alias established in line 25, the new BankAccount object is also inserted into s2. When we in line 34-35 iterate through all the CheckAccount objects of the set s2, we encounter an instance of BankAccount. We cannot carry out a SomeCheckAccountOperation on an instance of BankAccount.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | using System;
class SetOfAccounts{
public static void Main(){
// Construct accounts:
BankAccount ba1 = new BankAccount("John", 0.02),
ba2 = new BankAccount("Anne", 0.02),
ba3 = new BankAccount("Frank", 0.02);
CheckAccount ca1 = new CheckAccount("Mike", 0.03),
ca2 = new CheckAccount("Lene", 0.03),
ca3 = new CheckAccount("Joan", 0.03);
// Constructs empty sets of accounts:
Set<BankAccount> s1 = new Set<BankAccount>();
Set<CheckAccount> s2 = new Set<CheckAccount>();
// Insert elements in the sets:
s1.Insert(ba1); s1.Insert(ba2);
s2.Insert(ca1); s2.Insert(ca2);
// Establish s1 as an alias to s2
s1 = s2; // Compile-time error:
// Cannot implicitly convert type 'Set<CheckAccount>'
// to 'Set<BankAccount>'
// Insert a BankAccount object into s1,
// and via the alias also in s2
s1.Insert(new BankAccount("Bodil", 0.02));
// Activates some CheckAccount operation on a BankAccount object
foreach(CheckAccount ca in s2)
ca.SomeCheckAccountOperation();
Console.WriteLine("Set of BankAccount: {0}", s1);
Console.WriteLine("Set of CheckAccount: {0}", s2);
}
} | |||
|
The experimental insight obtained above is - perhaps - against our intuition. It can be argued that an instance of Set<CheckAccount> should be a valid stand in for an instance of Set<BankAccount>, as attempted in line 25. On the other hand, it can be asked if the extension of Set<CheckAccount> is a subset of Set<BankAccount>. (See Section 25.2 for a definition of extension). Or asked in this way: Is the set of set of check accounts a subset of a set of set of bank accounts? As designed in Section 25.3 the set of CheckAccounts is a subset of the set of BankAccount. But this does not imply that the set of set of CheckAccount is a subset of the set of set of BankAccount. A set of CheckAccount (understood as a single objects) is incompatible with a set of BankAccount (understood as a single object).
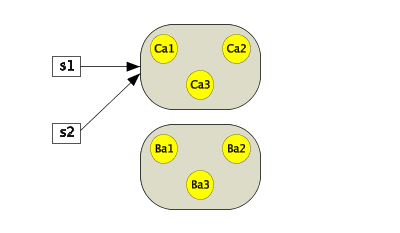
| Figure 42.1 A set of bank accounts and a set of check accounts |
In Program 42.10 we establish the scene illustrated in Figure 42.1. More precisely, the illustration shows the situation as of line 28 of Program 42.10. The problem is that we in line 31 add a new instance of BankAccount to s1, which refers to an instance of Set<CheckAccount>. Later in the program (line 35) this would cause "a minor explosion" if the program was allowed to reach this point . Thus, the real problem occurs if we mutate the set of check accounts that are referred from a variable of static type Set<BankAccount>. (See Section 28.10 for the definition of static type).
In general, we distinguish between the following kinds of variances in between Set<T> and T:
|
If Program 42.10 could be compiled and executed without problems (if line 25 is considered OK), then we would have covariance between Set<T> and T
In C# Set<T> is invariant in relation to T.
We notice that the problem discussed above is similar to the parameter variance problem, which we discussed in Section 29.2.
C# and Java do both agree on invariance in between Set<T> and T. But in contrast to C#, Java has a solution to the problem in terms of wildcard types. We realized above that Set<T> is not a generalization of all sets. In Java 1.5, a wildcard type written as Set<?> (a set of unknown) is a generalization of all sets. It is, however, not possible to mutate an object of static type Set<?>. If you are interested to known more about generics in Java, you should consult Gilad Bracha's tutorial "Generics in the Java Programming Language", [Bracha2004].
42.7. Generic structs
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
It is possible to make type parameterized structs, similar to the type parameterized classes that we have seen in the previous sections.
As an example we will see how we can define the generic struct Nullable<T> which defines the type behind the notation T? for an arbitrary value type T. Nullable types were discussed earlier in Section 14.9. Recall that nullable types enjoy particular compiler support, beyond the translation of T? to Nullable<T>. This includes support of lifted operators (operators that are extended to work on T? in addition to T) and support of the null value as such.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | using System;
public struct Nullable<T>
where T : struct{
private T value;
private bool hasValue;
public Nullable(T value){
this.value = value;
this.hasValue = true;
}
public bool HasValue{
get{
return hasValue;
}
}
public T Value{
get{
if(hasValue)
return value;
else throw new InvalidOperationException();
}
}
} | |||
|
The generic struct Nullable<T> aggregates a value of type T and a boolean value. The boolean value is stored in the boolean instance variable hasValue. If nv is of type Nullable<T> for some value type T, and if the variable hasValue of nv is false, then nv is considered to have the value null. The compiler arranges that the assignment nv = null is translated to nv.hasValue = false. This is somehow done behind the scene because hasValue is private.
42.8. Generic interfaces: IComparable<T>
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this section we will take a look at the generic interface IComparable<T>. We have earlier in the material (Section 31.5) studied the non-generic interface Icomparable, see Program 31.6.
If you review your solution to Exercise 8.6 you should be able to spot the weakness of a class ComparableDie, which implements IComparable. The weakness is that the parameter of the method CompareTo must have an Object as parameter. A method with the signature CompareTo(Die) does not implement the interface IComparable. (Due to static overloading of methods in C#, the methods CompareTo(Object) and CompareTo(Die) are two different methods, which just as well could have the signatures ObjectCompareTo(Object) and DieCompareTo(Die)). Thus, as given by the signature of CompareTo, we compare a Die and any possible object.
In Program 42.12 we reproduce IComparable<T>. Program 42.12 corresponds to Program 31.6. (Do not use any of these - both interfaces are parts of the System namespace). As it appears, in the generic interface the parameter of CompareTo is of type T. This alleviates the problem of the non-generic interface IComparable.
1 2 3 4 5 | using System;
public interface IComparable <T>{
int CompareTo(T other);
} | |||
|
Below we show a version of class Die which implements the interface IComparable<Die>. You should notice that this allows us to use Die as formal parameter of the method CompareTo.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | using System;
public class Die: IComparable<Die> {
private int numberOfEyes;
private Random randomNumberSupplier;
private const int maxNumberOfEyes = 6;
public Die(){
randomNumberSupplier = Random.Instance();
numberOfEyes = NewTossHowManyEyes();
}
public int CompareTo(Die other){
return this.numberOfEyes.CompareTo(other.numberOfEyes);
}
public void Toss(){
numberOfEyes = NewTossHowManyEyes();
}
private int NewTossHowManyEyes (){
return randomNumberSupplier.Next(1,maxNumberOfEyes + 1);
}
public int NumberOfEyes() {
return numberOfEyes;
}
public override String ToString(){
return String.Format("[{0}]", numberOfEyes);
}
}
public class Random {
// Singleton pattern:
// Keeps track of unique instance of this class
private static Random uniqueInstance = null;
// Holds the instance of System.Random
private System.Random systemRandom;
// Singleton pattern: Private constructor.
private Random(){
systemRandom = new System.Random(unchecked((int)DateTime.Now.Ticks));
}
public static Random Instance(){
if (uniqueInstance == null)
uniqueInstance = new Random();
return uniqueInstance;
}
public int Next(int lower, int upper){
// delegate to systemRandom
return systemRandom.Next(lower,upper);
}
}
class App{
public static void Main(){
Die[] dice = new Die[]{new Die(), new Die(), new Die(), new Die(),
new Die(), new Die(), new Die(), new Die(),
};
Console.WriteLine("Before sorting");
foreach(Die d in dice)
Console.Write("{0} ", d);
Console.WriteLine();
Console.WriteLine("After sorting");
Array.Sort(dice);
foreach(Die d in dice)
Console.Write("{0} ", d);
}
} | |||
|
The implementation of the generic interface is more type safe and
less clumsy than the implementation of the non-generic solution |
42.9. Generic equality interfaces
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
Before reading this section you may want to remind yourself about the fundamental equality operations in C#, see Section 13.5.
There exist a couple of generic interfaces which prescribes Equals operations. The most fundamental is IEquatable<T>, which prescribes a single Equals instance method. It may be attractive to implement IEquatable in certain structs, because it could avoid the need of boxing the struct value in order to make use of the inherited Equals method from class Object.
IEqualityComparer<T> is similar, but it also supports a GetHasCode method. (Notice also that the signatures of the Equals methods are different in the two interfaces. IEquatable<T> prescribes x.Equals(y) whereas IEqualityComparer<T> prescribes Equals(x,y)).
Below, in Program 42.14 and Program 42.15 we show reproductions of the two interfaces. Notice again that the two interfaces are present in the namespaces System and System.Collections.Generic respectively. Use them from there if you need them.
1 2 3 4 5 | using System;
public interface IEquatable <T>{
bool Equals (T other);
} | |||
|
1 2 3 4 5 6 | using System;
public interface IEqualityComparer <T>{
bool Equals (T x, T y);
int GetHashCode (T x);
} | |||
|
Several operations in generic collections, such as in List<T> in Section 45.9, need equality operations. The IndexOf method in List<T> is a concrete example, see Section 45.11. Using lst.IndexOf(el) we search for the element el in the list lst. Comparison of el with the elements of the list is done by the default equality comparer of the type T. The abstract generic class EqualityComparer<T> offers a static Default property. The Default property delivers the default equality comparer for type T. The abstract, generic class EqualityComparer<T> implements the interface IEqualityComparer<T>.
Unfortunately the relations between the generic interfaces IEquatable<T> and IEqualityComparer<T>, the class EqualityComparer<T> and its subclasses are quite complicated. It seems to be the cases that these interfaces and classes have been patched several times, during the evolution of versions of the .Net libraries. The final landscape of types is therefore more complicated than it could have been desired.
42.10. Generic Classes and Inheritance
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this section we will clarify inheritance relative to generic classes. We will answer the following questions:
Can a generic/non-generic class inherit from a non-generic/generic class? |
The legal and illegal subclassings are summarized below:
|
You can refresh the terminology (generic class/constructed class) in Section 42.2.
The rules are exemplified below.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | using System;
// A generic subclass of a non-generic superclass.
class SomeGenericSet1<T>: IntSet{
// ...
}
// A generic subclass of a constructed superclass
class SomeGenericSet2<T>: Set<int>{
// ...
}
// A generic subclass of a generic superclass
// The most realistic case
class SpecializedSet<T>: Set<T>{
// ...
}
// A non-generic subclass of a generic superclass
// Illegal. Compile-time error:
// The type or namespace name 'T' could not be found
class Set: Set<T>{
// ...
} | |||
|
From line 4 to 6 we are about to program a generic class SomeGenericSet1<T> based on a non-generic class IntSet. This particular task seems to be a difficult endeavor, but it is legal - in general - to use a non-generic class as a subclass of generic class.
Next, from line 9 to 11, we are about to program a generic class SomeGenericSet2<T> based on a constructed class Set<int>. This is also OK.
From line 15-17 we show the most realistic case. Here we program a generic class based on another generic class. In the specific example, we are about to specialize Set<T> to SpecializedSet<T>. The type parameter T of SpecializedSet<T> also becomes the type parameter of Set<T>. In general, it would also be allowed for SpecializedSet<T> to introduce additional type parameters, such as in SpecializedSet<T,S> : Set<T>.
The case shown from line 22 to 24 is illegal, simply because T is not the name of any known type. In line 22, T is name of an actual type parameter, but T is not around! It is most likely that the programmer is confused about the roles of formal and actual type parameters, see Section 42.2.
42.11. References
| [Bracha2004] | Gilad Bracha, "Generics in the Java Programming Language", July 2004. |
| [Golding05] | Tod Golding, Professional .NET 2.0 Generics. Wiley Publishing, Inc., 2005. |