   | Specialization, Extension, and Inheritance |
| A complete PDF version of the text book is now available. The PDF version is an almost complete subset of the HTML version (where only a few, long program listings have been removed). See here. |
   | Specialization, Extension, and Inheritance |
| A complete PDF version of the text book is now available. The PDF version is an almost complete subset of the HTML version (where only a few, long program listings have been removed). See here. |
In this section the topic is inheritance. Inheritance represents an organization of classes in which one class, say B, is defined on top of another class, say A. Class B inherits the members of class A, and in addition B can define its own members.
Use of inheritance makes it possible to reuse the data and operations of a class A in several so-called subclasses, such as B, C, and D, without coping these data and operations in the source code. Thus, if we modify class A we have also implicitly modified B, C and D.
There are several different views and understandings of inheritance, most dominantly specialization and extension. But also words such as subtyping and subclassing are used. We start our coverage by studying the idea of specialization.
25.1. Specialization of Classes
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
The idea of specialization was introduced in Section 3.4 when we studied concepts and phenomena. In Section 3.4 we defined a specialization as a more narrow concept than its generalization. We will, in this chapter, use the inspiration from specialization of concepts to introduce specialization of classes.
Classes are regarded as types, and specializations as subtypes Specialization facilitates definition of new classes from existing classes on a sound conceptual basis |
With specialization we nominate a subset of the objects in a type as a subtype. The objects in the subset are chosen such that they have "something in common". Typically, the objects in the subset are constrained in a certain way that set them apart from the surrounding set of objects.
We often illustrate the generalization/specialization relationship between classes or types in a tree/graph structure. See Figure 25.1. The arrow from B to A means that B is a specialization of A . Later we will use the same notation for the extended understanding that B inherits from A.

| Figure 25.1 The class B is a specialization of class A |
Below - in the dark blue definition box - we give a slightly more realistic and concrete definition of specialization. The idea of subsetting is reflected in the first element of the definition. The second element is, in reality a consequence of the subsetting. The last element stresses that some operations in the specialization can be redefined to take advantage of the properties that unite the objects/values in the specialization.
|
25.2. The extension of class specialization
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In Section 3.1 we defined the extension of a concept as the collection of phenomena that is covered by the concept. In this section we will also define the extension of a class, namely as the set of objects which are instances of the class or type.
We will now take a look at the extension of a specialized class/type. The subsetting idea from Section 25.1 can now be formulated with reference to the extension of the class.
The extension of a specialized class B
is a subset of the extension of the generalized class A |
The relationships between the extension of A and B can be illustrated as follows, using the well-known notation of wenn diagrams.

| Figure 25.2 The extension of a class A is narrowed when the class is specialized to B |
Let us now introduce the is-a relation between the two classes A and B:
|
The is-a relation characterizes specialization. We may even formulate an "is-a test" that tests if B is a specialization of A. The is-a relation can be seen as contrast to the has-a relation, which is connected to aggregation, see Section 3.3.
The is-a relation forms a contrast to the has-a relation The is-a relation characterizes specialization The has-a relation characterizes aggregation |
We will be more concrete with the is-a relation and the is-a test when we encounter examples in the forthcoming sections.
25.3. Example: Bank Accounts
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In Figure 25.3 we give three classes that specialize the class BankAccount.

| Figure 25.3 A specialization hierarchy of bank accounts |
The is-a test confirms that there is a generalization-specialization relationship between BankAccount and CheckAccount: The statement "CheckAccount is a BankAccount" captures - very satisfactory - the relationships between the two classes. The statement "BankAccount is a CheckAccount" is not correct, because we can imagine bank accounts which are not related to checks at all.
As a contrast, the has-a test fails: It is against our intuition that "a CheckAccount has a BankAccount". Similarly, it is not the case that "BankAccount has a CheckAccount". Thus, the relationship between the classes BankAccount and CheckAccount is not connected to aggregation/decomposition.
In Figure 25.4 we show a possible constellation of extensions of the bank account classes. As hinted in the illustration, the specialized bank accounts overlap in such a way that there can exist a bank account which is both a CheckAccount, a SavingsAccount, and a LotteryAccount. An overlapping like in Figure 25.4 is the prerequisite for (conceptually sound) multiple specialization, see Section 27.5.
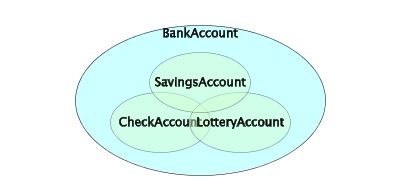
| Figure 25.4 Possible extensions of the bank account classes |
25.4. Example: Bank Accounts in C#
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this section we show some concrete C# bank account classes, corresponding to the classes introduced in Figure 25.3.
The BankAccount class in Program 25.1 is similar to the class introduced earlier in Program 11.5. We need, however, to prepare for specialization/inheritance in a couple of ways. We briefly mention these preparations here. The detailed treatment will be done in the following sections.
First, we use protected instance variables instead of private instance variables. This allows the instance variables to be seen in the specialized bank account classes. See Section 27.3 for details.
Next, we use the virtual modifier for the methods that are introduced in class BankAccount. This allows these methods to be redefined in the specialized bank account classes. See Section 28.9.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | using System;
public class BankAccount {
protected double interestRate;
protected string owner;
protected decimal balance;
public BankAccount(string o, decimal b, double ir) {
this.interestRate = ir;
this.owner = o;
this.balance = b;
}
public BankAccount(string o, double ir):
this(o, 0.0M, ir) {
}
public virtual decimal Balance {
get {return balance;}
}
public virtual void Withdraw (decimal amount) {
balance -= amount;
}
public virtual void Deposit (decimal amount) {
balance += amount;
}
public virtual void AddInterests() {
balance += balance * (Decimal)interestRate;
}
public override string ToString() {
return owner + "'s account holds " +
+ balance + " kroner";
}
} | |||
|
The CheckAccount class shown in Program 25.2 redefines (overrides) the Withdraw method. This gives a special meaning to money withdrawal from a CheckAccount object. The method ToString is is also redefined (overridden) in class CheckAccount, in the same way as it was overridden in class BankAccount relative to its superclass (Object), see Program 25.1.
Notice also the two constructors of class CheckAccount. They both delegate the construction work to BankAccount constructors via the base keyword. See Section 28.4 for details on constructors. This is similar to the delegation from one constructor to another in the same class, by use of this, as discussed in Section 12.4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | using System;
public class CheckAccount: BankAccount {
public CheckAccount(string o, double ir):
base(o, 0.0M, ir) {
}
public CheckAccount(string o, decimal b, double ir):
base(o, b, ir) {
}
public override void Withdraw (decimal amount) {
balance -= amount;
if (amount < balance)
interestRate = -0.10;
}
public override string ToString() {
return owner + "'s check account holds " +
+ balance + " kroner";
}
} | |||
|
The class SavingsAccount follow the same pattern as class CheckAccount. Notice that we also in class SavingsAccount redefine (override) the AddInterests method.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | using System;
public class SavingsAccount: BankAccount {
public SavingsAccount(string o, double ir):
base(o, 0.0M, ir) {
}
public SavingsAccount(string o, decimal b, double ir):
base(o, b, ir) {
}
public override void Withdraw (decimal amount) {
if (amount < balance)
balance -= amount;
else
throw new Exception("Cannot withdraw");
}
public override void AddInterests() {
balance = balance + balance * (decimal)interestRate
- 100.0M;
}
public override string ToString() {
return owner + "'s savings account holds " +
+ balance + " kroner";
}
} | |||
|
In the class LotteryAccount the method AddInterests is redefined (overridden). The idea behind a lottery account is that a few lucky accounts get a substantial amount of interests, whereas the majority of the accounts get no interests at all. This is provided for by the private instance variable lottery, which refers to a Lottery object.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | using System;
public class LotteryAccount: BankAccount {
private static Lottery lottery = Lottery.Instance(20);
public LotteryAccount(string o, decimal b):
base(o, b, 0.0) {
}
public override void AddInterests() {
int luckyNumber = lottery.DrawLotteryNumber;
balance = balance + lottery.AmountWon(luckyNumber);
}
public override string ToString() {
return owner + "'s lottery account holds " +
+ balance + " kroner";
}
} | |||
|
An instance of the Lottery class controls the randomness (the lottery aspect) and the size of the amount won (through the method AmountWon, and in turn the method DrawLotteryNumber). For completeness the Lottery class is shown in Program 25.5 (only on web). Using our experience with Random objects from Section 10.1 we have programmed the class Lottery in Program 25.5 as a Singleton. For details about the Singleton design pattern see Section 16.3.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | using System;
public class Lottery{
private static Random rdm =
new Random(unchecked((int)DateTime.Now.Ticks));
private int difficulty;
private readonly int winningNumber;
private readonly decimal amountWon;
private static Lottery uniqueInstance = null;
private Lottery(int difficulty){
this.difficulty = difficulty;
this.winningNumber = rdm.Next(difficulty);
this.amountWon = 500000.00M;
}
public static Lottery Instance(int difficulty){
if (uniqueInstance == null)
uniqueInstance = new Lottery(difficulty);
return uniqueInstance;
}
public int DrawLotteryNumber{
get {return rdm.Next(difficulty);}
}
public decimal AmountWon(int luckyNumber){
decimal res;
if (WinningNumber(luckyNumber))
res = amountWon;
else
res = 0.0M;
return res;
}
private bool WinningNumber(int n){
return n == winningNumber;
}
} | |||
|
25.5. Example: Geometric Shapes
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
In this section we show another example of specialization. The tree in Figure 25.5 illustrates a number of specializations of polygons. In the left branch of the tree we see the traditional and complete hierarchy of triangle types. In the right branch we show the most important specializations of quadrangles. Trapezoids are assumed to have exactly one pair of parallel sides, and as such trapezoids and parallelograms are disjoint.
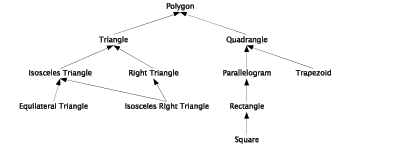
| Figure 25.5 A specialization hierarchy of polygons |
The polygon type hierarchy is a typical specialization hierarchy, because it fully complies with the definition of specialization from Section 25.1. The subset relationship is easy to verify. All operations defined at the polygon level are also available and meaningful on the specialized levels. In addition it makes sense to redefine many of the operations to obtain more accurate formula behind the calculations.
Overall, the deeper we come in the hierarchy, the more constraints apply. This is a typical characteristic of a real and pure generalization/specialization class hierarchy.
25.6. Specialization of classes
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
We will now summarize the idea of class specialization. Objects of specialized classes
|
Specialization of classes in pure form do not occur very often. Specialization in combination with extension is much more typical. |
As noticed in Section 25.4 the hierarchy of polygons is real and pure example of specialization hierarchy.
The bank account hierarchy in Figure 25.3 is not as pure as the polygon hierarchy. The bank account hierarchy is - in the starting point - a specialization hierarchy, but the specialized classes are likely to be extended with operations, which do not make sense in the BankAccount class. Class extension is the topic in Chapter 26.
25.7. The Principle of Substitution
Contents Up Previous Next Slide Annotated slide Aggregated slides Subject index Program index Exercise index
The principle of substitution is described by Timothy Budd in section 8.3 of in his book An Introduction to Object-oriented Programming [Budd02]. The principle of substitution describes an ideal, which not always is in harmony with our practical and everyday programming experience. This corresponds to our observation that pure specialization only rarely is found in real-life programs.
|
As an example, consider the class hierarchy of polygons in Figure 25.5. Imagine that we have the following scene:
Polygon p = new Polygon(...); RightTriangle tr = new RightTriangle(...); /* Rest of program */
It is now possible to substitute the polygon object with the triangle object in the "rest of the program". This is possible because the triangle possesses all the general properties (area, circumference, etc) of the polygon. At least, the compiler will not complain, and the executing program will not halt. Notice, however, that the substitution is only neutral to the actual meaning of the execution program if the replaced polygon actually happens to be the appropriate right triangle!
Notice that the opposite substitution does not always work. Thus, we cannot substitute a triangle with a general polygon (for instance a square). Most programs would break immediately if that was attempted. The reason is that a square does not, in general, possess the same properties as a triangle.
The ideas behind the principle of substitution are related to virtual methods (Section 28.14) and to dynamic binding (Section 28.11).
25.8. References
| [Budd02] | Timothy Budd, An Introduction to Object-Oriented Programming, third edition. Pearson. Addison Wesley, 2002. |