


   | The Order of Evaluation |
As noticed in Chapter 19 and Chapter 20 the evaluation strategy in Scheme is the one called applicative order, cf. Section 20.6.
In contrast to normal-order reduction and lazy evaluation - as described in Section 20.6 and Section 20.11 - we can think of Scheme as eager in the evaluation of the function parameters.
In this chapter we will see how to make use of a new evaluation idea in terms of explicitly delaying the evaluation of certain expressions. This is the topic of Section 21.1 and Section 21.2.
21.1. Delayed evaluation in Scheme
Contents Up Previous Next Slide Subject index Program index Exercise index
The starting point of our discussion is now clear.
Scheme does not support normal-order reduction nor lazy evaluation Scheme has an explicit primitive which delays an evaluation |
The delay and force primitives are described in Syntax 21.1 and Syntax 21.2. The delay primitive returns a so-called promise, which can be redeemed by the force primitive. Thus, the composition of delay and force carry out a normal evaluation step.
| |||
|
| |||
|
In Program 21.1 we show simple implementations of delay and force. In Program 21.2 we show possible implementations of delay by means of Scheme macros.
1 2 3 | (delay expr) ~ (lambda() expr) (define (force promise) (promise)) | |||
|
The thing to notice is the semantic idea behind the implementation of delay. The expression (delay expr) is equivalent to the expression (lambda () expr). The first expression is supposed to replace the other expression at program source level. The value of the lambda expression is a closure, cf. Section 8.11, which captures free names in its context together with the syntactic form of expr. As it appears from the definition of the function force in Program 21.1 the promise returned by the delay form is redeemed by calling the parameter less function object. It is easy to see that this carries out the evaluation of expr.
Be sure to observe that force can be implemented by a function, whereas delay cannot. The reason is, of course, that we cannot allow a functional implementation of delay to evaluate the parameter of delay. The whole point of delay is to avoid such evaluation. This rules out an implementation of delay as a function. The force primitive, on the other hand, can be implemented by a function, because it works on the value of a lambda expression.
Please notice that other implementations of delay and force can easily be imagined. The Scheme Report describes language implementations of delay and force, which may use other means than described above to obtain the same semantic effect, cf. [delay-primitive] and [force-primitive].
1 2 3 4 5 6 7 8 9 10 11 | ; R5RS syntactic abstraction:
(define-syntax my-delay
(syntax-rules ()
((delay expr)
(lambda ()
expr))))
; MzScheme syntactic abstraction:
(define-macro my-delay
(lambda (expr)
`(lambda () ,expr))) | |||
|
21.2. Examples of delayed evaluation
Contents Up Previous Next Slide Subject index Program index Exercise index
Let us look at a few very simple examples of using delay and force. In the first line of the table below we delay the expression (+ 5 6). The value is a promise that enables us to evaluate the sum when necessary, i.e, when we choose to force it. The next line shows that we cannot force a non-promise value. The last line shows an immediate forcing of the promise, which we bind to the name delayed in the let construct.
| Expression | Value |
(delay (+ 5 6)) | #<promise> |
(force 11) | error |
(let ((delayed (delay (+ 5 6)))) (force delayed)) | 11 |
| Table 21.1 Examples of use of delay and force. |
21.3. Infinite lists in Scheme: Streams
Contents Up Previous Next Slide Subject index Program index Exercise index
We are now done with the toy examples. It is time to use delayed evaluation in Scheme to something of real value. In this material we focus on streams. A stream is an infinite list. The inspiration to our coverage of streams comes directly from the book Structure and Interpretation of Computer Programs [Abelson98].
The crucial observation is the following.
We can work with lists of infinite length by delaying the evaluation of every list tail using delay As an invariant, every list tail will be delayed |
Every tail of a list is a promise. The promise covers an evaluation which gives a new cons cell, in which the tail contains another promise.
It is simple to define a vocabulary of stream functions. There is an obvious relationship between list functions (see Section 6.1) and the stream functions shown below in Program 21.3.
1 2 3 4 5 6 7 8 9 10 | (cons-stream a b) ~ (cons a (delay b)) (define head car) (define (tail stream) (force (cdr stream))) (define empty-stream? null?) (define the-empty-stream '()) | |||
|
In that same way as we defined delay as a macro in Program 21.2 , we also need to define cons-stream as a macro. The reason is that we are not allowed to evaluate the second parameter; The second parameter of cons-cell is going to be delayed, and as such it must be passed unevaluated to cons-stream.
1 2 3 4 | (define-syntax cons-stream
(syntax-rules ()
((cons-stream x y)
(cons x (delay y))))) | |||
|
In the following sections we will study a number of interesting examples of streams from the numerical domain.
21.4. Example streams
Contents Up Previous Next Slide Subject index Program index Exercise index
In the first example line in Table 21.2 we define a stream of ones. In other words, the name ones is bound to an infinite list of ones: (1 1 1 ...).
Please notice the very direct use of recursion in the definition of ones. We are used to a conditional such as cond or if when we deal with recursion, in order to identify a basis case which stops the recursive evaluation process. We do not have such a construction here. The reason is that we never reach any basis (or terminating case) of the reduction. Due to the use of delayed evaluation we never attempt to expand the entire list. Instead, there is a promise in the end of the list which can deliver more elements if needed.
In the second row of the example we use the function stream-section to extract a certain prefix of the list (determined by the first parameter of stream-section). The function stream-section is defined in Program 21.5 together with another useful stream function called add-streams which adds elements of two numeric streams together.
In the third row we define a stream of all natural numbers, using the function integers-starting-from .
The fourth row shows an alternative definition of nat-nums. We use add-streams on nat-nums and ones to produce nat-nums. Please notice the recursion which is involved.
In the bottom row of the table we define the Fibonacci numbers, in a way similar to the definition of nat-nums just above. fibs is defined by adding fibs to its own tail. This works out because we provide enough staring numbers (0 1) to get the process started.
| Expression | Value |
(define ones (cons-stream 1 ones)) | (1 . #<promise>) |
(stream-section 7 ones) | (1 1 1 1 1 1 1) |
(define (integers-starting-from n) (cons-stream n (integers-starting-from (+ n 1)))) (define nat-nums (integers-starting-from 1)) (stream-section 10 nat-nums) | (1 2 3 4 5 6 7 8 9 10) |
(define nat-nums (cons-stream 1 (add-streams ones nat-nums))) (stream-section 10 nat-nums) | (1 2 3 4 5 6 7 8 9 10) |
(define fibs
(cons-stream 0
(cons-stream 1
(add-streams (tail fibs) fibs))))
(stream-section 15 fibs) | (0 1 1 2 3 5 8 13 21 34 55 89 144 233 377) |
| Table 21.2 Examples of streams. ones is an infinite streams of the element 1. stream-section is a function that returns a finite section of a potentially infinite stream. nat-nums is stream of all the natural numbers, made by use of the recursive function integers-starting-from. The fourth row shows an alternative definition of nat-nums. Finally, fibs is the infinite stream of Fibonacci numbers. |
As mentioned above, the functions stream-section and add-streams in Program 21.5 are used in Table 21.2.
In the web version of the material (slide and annotated slide view) there is an additional program with all the necessary definitions which allow you to play with streams in MzScheme or DrScheme.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | (define (stream-section n stream)
(cond ((= n 0) '())
(else
(cons
(head stream)
(stream-section
(- n 1)
(tail stream))))))
(define (add-streams s1 s2)
(let ((h1 (head s1))
(h2 (head s2)))
(cons-stream
(+ h1 h2)
(add-streams (tail s1) (tail s2))))) | |||
|
21.5. Stream example: The sieve of Eratosthenes
Contents Up Previous Next Slide Subject index Program index Exercise index
Still with direct inspiration from the book Structure and Interpretation of Computer Programs [Abelson98] we will look at a slightly more complicated example, namely generation of the stream of prime numbers. This is an infinite list, because the set of prime numbers is not finite.
The algorithmic idea behind the generation of prime numbers, see Program 21.6 was originally conceived by Eratosthenes (a Greek mathematician, astronomer, and geographer who devised a map of the world and estimated the circumference of the earth and the distance to the moon and the sun - according to the American Heritage Dictionary of the English Language).
The input of the function sieve in Program 21.6 is the natural numbers starting from 2. See also the example in Table 21.3. The first element in the input is taken to be a prime number. Let us say the first such number is p. No number p*n, where n is a natural number greater than one, can then be a prime number. Program 21.6 sets up a sieve which disregards such numbers.
Recursively, the first number which comes out of the actual chain of sieves is a prime number, and it is used set up a new filter. This is due to the simple fact that the sieve function calls itself.
The Sieve of Eratosthenes is a more sophisticated example of the use of streams |
1 2 3 4 5 6 7 | (define (sieve stream)
(cons-stream
(head stream)
(sieve
(filter-stream
(lambda (x) (not (divisible? x (head stream))))
(tail stream))))) | |||
|
Program 21.6 uses the functions cons-stream, head and tail from Program 21.3. The functions filter-stream and divisible? are defined in Program 21.7.
Figure Figure 21.1 shows a number of sieves, and it sketches the way the numbers (2 3 4 ...) are sieved. Notice that an infinite numbers of sieves are set up - on demand - when we in the end requests prime numbers.
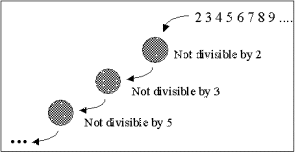
| Figure 21.1 An illustration of the generation of prime numbers in The Sieve of Eratosthenes |
21.6. Applications of The sieve of Eratosthenes
Contents Up Previous Next Slide Subject index Program index Exercise index
In this section we show an example of prime number generation with the sieve function from Program 21.6.
Notice that the prime numbers are really generated on demand. In the call (stream-section 25 primes) we are requesting 25 prime numbers. This triggers generation of sufficient natural numbers via (integers-starting-from 2), and it triggers the set up of sufficient sieves to produce the result.
We see that the evaluations are done on demand.
The sieve process produces the stream of all prime numbers |
| Expression | Value |
(define primes
(sieve
(integers-starting-from 2)))
(stream-section 25 primes) | (2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97) |
| Table 21.3 The first 25 prime numbers made by sieving a sufficiently long prefix of the integers starting from 2. |
You can use the definitions in Program 21.7 to play with the sieve function. You should first load the stream stuff discussed in Section 21.4. More specifically, you should load the definitions on the last program clause in the slide view of Section 21.4. Then load the definitions in Program 21.7.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | (define (sieve stream)
(cons-stream
(head stream)
(sieve
(filter-stream
(lambda (x) (not (divisible? x (head stream))))
(tail stream)))))
(define (divisible? x y)
(= (remainder x y) 0))
(define (filter-stream p lst)
(cond ((empty-stream? lst) the-empty-stream)
((p (head lst)) (cons-stream (head lst) (filter-stream p (tail lst))))
(else (filter-stream p (tail lst)))))
(define (integers-starting-from n)
(cons-stream n
(integers-starting-from (+ n 1))))
(define primes (sieve (integers-starting-from 2))) | |||
|
21.7. References
| [Abelson98] | Richard Kelsey, William Clinger and Jonathan Rees, "Revised^5 Report on the Algorithmic Language Scheme", Higher-Order and Symbolic Computation, Vol. 11, No. 1, August 1998, pp. 7--105. |
| [Delay-primitive] | R5RS: delay http://www.cs.auc.dk/~normark/prog3-03/external-material/r5rs/r5rs-html/r5rs_36.html#SEC38 |
| [Force-primitive] | R5RS: force http://www.cs.auc.dk/~normark/prog3-03/external-material/r5rs/r5rs-html/r5rs_63.html#SEC65 |