


   | The Order of Evaluation |
At this point in the material we start our coverage of evaluation order. We start by discussing the idea of referential transparency.
| 19.1 Referential transparency | 19.4 A motivating example |
| 19.2 An illustration of referential transparency | 19.5 A motivating example - clarification |
| 19.3 Arbitrary evaluation order - with some limits |
19.1. Referential transparency
Contents Up Previous Next Slide Subject index Program index Exercise index
The main idea behind the concept of referential transparency is captured by the point below.
Two equal expressions can substitute each other without affecting the meaning of a functional program |
As formulated above, the possibility of substituting one expression by another depends on whether or not the two expressions are considered as being equal. As noticed in Section 4.5 there are a number of different interpretations of equality around in Scheme, as well as in other programming languages.
As we observe in the items below, we can use even the weakest form of equality, namely structural, deep equality, for our observations about referential transparency. In other words, if two structures are structurally equal, the expressions and values involved may substitute each other.
|
The idea of referential transparency can be stated very briefly in the following way:
Equals can be replaced by equals |
19.2. An illustration of referential transparency
Contents Up Previous Next Slide Subject index Program index Exercise index
Before we proceed we will illustrate some practical uses of referential transparency.
With referential transparency it is possible to perform natural program transformations without
any concern of side effects |
The two expressions in the top left and the top right boxes of Figure 19.1 may substitute each other, provided that the function F is a pure function (without side effects).
In the case where F is a value returning procedure, as illustrated in the bottom box of Figure 19.1 it is clear that it is important how many times F is actually evaluated. The reason is that an evaluation of F affects the value of the variable c, which is used in the top level expressions. (Thus, F is an imperative abstraction - a procedure).
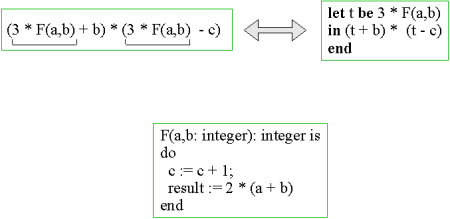
| Figure 19.1 It is possible to rewrite one of the expressions above to the other, provided that F is a function. Below, we have illustrated an example where F is of procedural nature. Notice that F assigns the variable c, such that it becomes critical to know how many times F is called. |
On the ground of this example it is worth observing that equational reasoning about functional programs is relatively straightforward. If procedures are involved, as F in the bottom box of Figure 19.1, it is much harder to reason about the expression, for instance with the purpose of simplifying it (as it is the case when substituting the expression to the left with the expression to the right in the top-part of Figure 19.1).
19.3. Arbitrary evaluation order - with some limits
Contents Up Previous Next Slide Subject index Program index Exercise index
In this section we will discuss the order of subexpression evaluation in a composite expression.
In a functional program an expression is evaluated with the purpose of producing a value An expression is composed of subexpressions |
Take a look at one of the expressions in Figure 19.2. The underlying syntax trees are shown below the expressions in the figure. The question is which of the subexpressions to evaluate first, which comes next, and which one is to be the last.

| Figure 19.2 An illustration of an expression with subexpressions. |
To be concrete, we can propose to start from the left leaf, from the right leaf, from the top, or perhaps from some location in the middle of the expression.
In the functional programming context, with expressions and pure functions, we will probably expect that an arbitrary evaluation order is possible. If we should devise a practical recipe we will probably start from one of leafs (say the leftmost leaf) and work our way to the expression in the root.
As noticed below, we can actually use an arbitrary evaluation order, provided that there are no errors in any of the subexpressions, and provided that all of the involved evaluations terminate.
|
In the rest of this section, as well as in Chapter 20 we will study and understand the premises and the limits of 'arbitrary evaluation order'.
19.4. A motivating example
Contents Up Previous Next Slide Subject index Program index Exercise index
It is valuable to understand the problems and the quirks of evaluation order by looking at a very simple program example.
What is the value of the following expression? |
The lambda expression in Program 19.1 shows a pseudo application of the constant function, which returns 1 for every possible input x. The tricky part is, however, that we pass an actual parameter expression which never terminates.
1 | ((lambda (x) 1) some-infinite-calculation) | |||
|
It is not difficult to write a concrete Scheme program, which behave in the same way as Program 19.1. Such a program is shown in Program 19.2. The parameter less function infinite-calculation just calls itself forever recursively.
1 2 3 4 | (define (infinite-calculation) (infinite-calculation)) ((lambda (x) 1) (infinite-calculation)) | |||
|
19.5. A motivating example - clarification
Contents Up Previous Next Slide Subject index Program index Exercise index
As noticed below, it can be argued that the value of the expression in Program 19.1 is 1, due to the reasoning that the the result of the function (lambda (x) 1) is independent of the formal parameter x.
It can also be argued that an evaluation of the actual parameter expression (infinite-calculation) stalls the evaluation of the surrounding expression, such that the expression in Program 19.1 does not terminate. In Scheme, as well as in most other programming languages, this will be the outcome.
The items below summarizes these two possibilities, and they introduce two names of the two different function semantics, which are involved.
|
In most languages, functions are strict. This is also the case in Scheme. In some languages, however, such as Haskell and Miranda, functions are non-strict. As we will see in the following, languages with non-strict functions are very interesting, and they open up new computational possibilities.