In this chapter we will review inheritance - including specialization - in the light of contracts. Specialization was discussed in Chapter 25 and inheritance was discussed in Chapter 27. The concept of contracts was introduced in Chapter 51.

Stated briefly, we understand a subclass as a subcontractor of its superclass. Being a subcontractor, it will not be possible to carry out arbitrary redefinitions of operations in a subclass, relative to the overridden operations in the superclass.

53.1 Inheritance and Contracts 53.3 Class invariants in the triangle class hierarchy 53.2 Subcontracting 53.4 Assertions in Abstract classes

 

53.1.  Inheritance and Contracts
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

The following question is of central importance to the discussion in this chapter.

Figure 53.1 illustrates a class B which inherits from class A. Both class A and B have invariants. In addition, operations in class A that are redefined in class B have preconditions as well as postconditions.

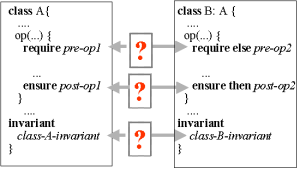
Figure 53.1    The relationship between inheritance and contracts

The question from above can now to refined as follows:

• How is the invariant in class B related to the invariant of class A?
• How is the precondition of the operation op in class B related to the precondition of the overridden operation op from class A?
• How is the postcondition of the operation op in class B related to the postcondition of the overridden operation op from class A?

Each of the three questions are symbolized with a red question mark in Figure 53.1.

53.2.  Subcontracting
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

Due to polymorphism, an instance of a subclass can act as a stand in for - or subcontractor of - an instance of the superclass. Consequently, the contract of the subclass must comply with the contract of the superclass. The contract of a subclass must therefore be a subcontract of the superclass' contract. This is closely related to the principle of substitution, which we discussed in Section 25.7.

The notion of subcontracting is realized by enforcing particular requirements to preconditions, postconditions, and class invariants across class hierarchies. In order to understand inheritance as subcontracting, the following rules must apply for assertions in a subclass:

The precondition must not be stronger than the precondition in the superclass The postcondition must not be weaker than the postcondition in the superclass The class invariant must not be weaker than the invariant in the superclass

As discussed in Section 50.1, a precondition of an operation states the prerequisites for calling the operation. If the precondition is evaluated to the value true, the operation can be called. It is the responsibility of the caller (the client) to fulfill the precondition. The postcondition of the operation states the meaning of the operation, in terms of requirements to the returned value and/or requirements to the effect of the operation. It is the responsibility of the operation itself (the server) to fulfill the postcondition. The postcondition must be true if the precondition is satisfied and if the operation terminates normally (without throwing an exception).

If we assume that the precondition of a redefined operation in a subclass is stronger than the precondition of the original operation in the superclass, then the subclass cannot be used as a subcontractor of the superclass. Consequently, the preconditions of redefined operations in subclasses must be equal to or weaker than the preconditions of corresponding operations in superclasses.

In case the postcondition of a redefined operation in a subclass is weaker than the postcondition of the operation in the superclass, the redefined operation does not solve the problem as promised by the contract in the superclass. Therefore, the postconditions of redefined operations must be equal to or stronger than the postconditions of corresponding operations in superclasses.

The superclass has promised to solve some problem via the virtual operations. Redefined and overridden operations in subclasses are obliged to solve the problem under the same, or possible weaker conditions. This causes the weakening of preconditions. The job done by the redefined and overridden operations must be as least as good as promised in the superclass. This causes the strengthening of postconditions.

The invariant of the superclass expresses requirements to instance variables in the superclass, at stable points in time. These instance variables are also present in subclasses, and the requirements to these persist in subclasses. Consequently, class invariants cannot be be weakened in subclasses.

Relative to Figure 53.1 the formulated precondition pre-op2 in B.op serves as a weakening of pre-op1 of A.op. The effective precondition of B.op is pre-op1 or pre-op2. Similarly, the effective postcondition of B.op2 is post-op1 and post-op2. The use of the Eiffel keywords require else and ensure then signals this understanding.

In our discussion of redefinition of methods in Section 28.9 we came up with some technical and syntactical requirements to redefinitions. The contributions outlined above in terms of subcontracting constrain the meaning (the semantics) of redefined operations in subclasses in relation to the original operations in superclasses. This is very satisfactory!

53.3.  Class invariants in the triangle class hierarchy
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

We studied the specialization hierarchy of polygons in Section 25.5. In Figure 53.1 below we revisit the five triangle classes. It is our interest to understand how the class invariants are strengthened in subclasses of the most general triangle class.

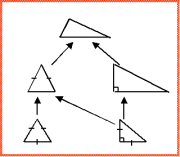
Figure 53.2    The hierarchy of triangle classes. The root class represents the most general triangle. The son to the left represents an isosceles triangle (where two sides are equal lengths). The son to the right represents a right triangle, where one of the angles is 90 degrees. The triangle at the bottom left is an equilateral trianlge (where all three sides are of equal lengths). The triangle at the bottom right is both an isosceles triangle and a right triangle.

The invariants of the five types of triangles can be described as follows:

• Most general triangle:
  3 angles, 3 edges
  Sum of angles: 180 degrees
• Isosceles triangle
  Invariant of general triangle
  2 edges of equal length
• Equilateral triangle:
  Invariant of isosceles triangle
  3 edges of equal length
• Right triangle:
  Invariant of general triangle
  Pythagoras
• Isosceles right triangle:
  Invariant of isosceles triangle
  Invariant of right triangle
  

Notice that the italic contributions above describe the strengthenings relative to the invariant of the superclass.

53.4.  Assertions in Abstract classes
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

Abstract classes where discussed in Section 30.1. An abstract method in an abstract class defines the name and parameters of the method - and nothing more. The intended meaning of the method is an informal matter. In Chapter 30 we did not encounter any means to define or constrain the actual result or effect of abstract methods. In this section we will see how the meaning of an abstract method can be specified.

In Program 30.1 we studied an abstract class Stack. Below, in Program 53.1 we show a version of the abstract stack with contractual elements - preconditions and postconditions. Possible future non-abstract subclasses of Stack will be subcontractors. It means that such subclasses will have to fulfill the contract of the abstract stack, in the way we have discussed in Section 53.2.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

using System;

public abstract class Stack{ 
  
  abstract public void Push(Object el);
    require !full;   
    ensure  !empty  &&  top() = el  &&  size() = old size() + 1 &&
            "all elements below el are unaffected";   

  abstract public void Pop();
    require !empty();   
    ensure  !full()  &&  size() = old size() - 1 &&
            "all elements remaining are unaffected";   

  abstract public Object Top
    require !empty();   
    ensure  nochange  &&  Top = "the most recently pushed element";    {  
    get; }


  abstract public bool Full
    require true;   
    ensure nochange  &&  Full = (size() = capacity);   {
    get; }


  abstract public bool Empty 
    require true;   
    ensure nochange  &&  Empty = (size() = 0);   {
    get;}

  abstract public int Size
    require true;   
    ensure nochange  &&  Size = "number of elements on stack";   {
    get;}   

  public void ToggleTop()
    require size() >= 2;   {
    if (Size >= 2){
      Object topEl1 = Top;  Pop();
      Object topEl2 = Top;  Pop();
      Push(topEl1); Push(topEl2);
    }
    ensure size() = old size() && 
    "top and element below top have been exchanged"  &&
    "all other elements are unaffected";       
  }   

  public override String ToString(){
    return("Stack");
  }
}

As we have seen before, require clauses are preconditions and ensure clauses are postconditions. Notice the use of old and nochange, which we introduced in Section 50.2. The "italic strings" represent informal preconditions. Alternatively, and more rigidly, we may consider to implement these parts of the assertions as private boolean functions. Notice, however, that it would be quite demanding to do so, at least compared with the remaining implementation efforts involved.