As exemplified at the end of the previous chapter, preconditions and postconditions can be used to specify the meaning of a function. In this chapter we will study preconditions and postconditions in more details.

50.1 Logical expressions 50.3 An Assertion Language 50.2 Examples of preconditions and postconditions

 

50.1.  Logical expressions
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

Logical expressions and assertions form the basis of preconditions and postconditions. Consequently, we define the concepts of logical expressions and assertions before preconditions and postconditions:

We have worked with logical expressions numerous times during this course. Logical expressions are formed by relational, equational, conjunctional (and) and disjunctional (or) operators. You find these operators at level 3, 4, 8, and 9 in Table 6.1.

Assertions are also used in the context of program testing. In Section 55.7 we surveyed a large collection of assertions, which are available in the NUnit testing tools for C#. As stated in Section 55.8, an assertion in a test case, which returns the value false, causes a failure. A failed testcase signals that the unit under test is incorrect. Assertions used in test cases are similar to assertions found in postconditions.

We can now characterize a precondition in the following way:

A precondition states if it makes sense to call an operation The precondition is a prerequisite for the activation

The precondition is typically formulated in terms of the formal parameters of the operation.

Similarly, a postcondition can be characterized as follows:

A postcondition states if the operation returns the desired result, or has the desired effect, relative to the given parameters that satisfy the precondition The postcondition defines the meaning of the operation

The postcondition of a procedure or function F must be fulfilled if the precondition of F holds, and if F terminates (F runs to its completion).

50.2.  Examples of preconditions and postconditions
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

We will now study preconditions and postconditions of the operations in a circular list. A circular list is a linked list, in the sense we discussed in Section 45.14. However, the circular list discussed in this section is only single-linked. The distinctive characteristics of a circular list are the following:

1. The last LinkedListNode is linked to the first LinkedListNode of the list
2. The CircularList object refers to the LinkedListNode of the last element instead of the LinkedListNode of the first element.

We show a circular list with five elements in Figure 50.1. The idea of referring the last element instead of the first element from the CircularList object means that both the front and the rear of the list can be reached in constant time. In many context, this is a very useful property. Notice also, that it is possible to deal with double-linked circular lists as well.

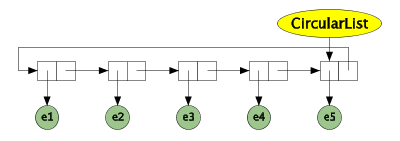
Figure 50.1    A circular list. The large yellow object represents the circular list as such. The circular green nodes represent the elements of the list. The rectangular nodes are instances of a class akin to LinkedListNode, which connect the constituents of the list together.

Below we specify the operations of the circular list with preconditions and postconditions. The specification in Program 50.1 defines the meaning of operations of the yellow object in Figure 50.1. In the program listing, the preconditions are marked with keyword require, and shown in red. The postconditions are marked with the keyword ensure, and shown in blue. The names of the keywords stem from the object-oriented programming language Eiffel [Meyer97, Meyer92, Switzer93], which is strong in the area of assertions. Apart from that, the syntax used in Program 50.1 is C# and Java like.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

class CircularList {

  // Construct an empty circular list 
  public CircularList()
    require true;  
    ensure Empty();  

  // Return my number of elements 
  public int Size()
    require true;  
    ensure size = CountElements() && noChange;  

  // Insert el as a new first element 
  public void InsertFirst(Object el)
    require !Full();  
    ensure !Empty() && IsCircular() && IsFirst(el);  
     
  // Insert el as a new last element 
  public void InsertLast(Object el)
    require !Full();  
    ensure !Empty() && IsCircular() && IsLast(el);  

  // Delete my first element 
  public void DeleteFirst()
    require !Empty();  
    ensure 
      Empty() || 
      (IsCircular() && IsFirst(old RetrieveSecond()));  

  // Delete my last element 
  public void DeleteLast()
    require !Empty();  
    ensure 
      Empty() || 
      (IsCircular() && isLast(old RetrieveButLast()));  

  // Return the first element in the list 
  Object RetrieveFirst()
    require !Empty();  
    ensure IsFirst(result) && noChange;  

  // Return the last element in the list 
  Object RetrieveLast()
    require !Empty();  
    ensure IsLast(result) && noChange;  
}

The precondition true of the constructor says that there are no particular requirements to call the constructor. This is natural and typical. The postcondition of the constructor expresses that the constructor makes an empty circular list.

The operation Size returns an integer corresponding to the counted number of elements in the list. CountElements is an operation, which counts the elements in the list. In a particular implementation of CircularList, the operation Size my return the value of a private instance variable which keeps track of the total number of elements in the list. nochange is a special assertion, which ensures that the state of the list has not changed due the execution of the Size operation. We see that the postcondition expresses the consistency between the value returned by Size, and the counted number of elements in the list.

The operation InsertFirst is supposed to insert an element, to become the first element of the list (the one shown at the left hand side of Figure 50.1). The precondition expresses that the list must not be full before the insertion. The postcondition expresses that the list is not empty after the insertion, that it is still circular, and that el indeed is the first element of the list. The specification of the operation InsertLast is similar to InsertFirst.

The operation DeleteFirst requires as a precondition a non-empty list. The postcondition of DeleteFirst expresses that the list either is empty or circular. If the list is non-empty (and therefore circular) after the deletion, the second element before the deletion must be the first element after the deletion. Notice the modifier old. The value of Old(expression) is the value of expression, as evaluated in the state just before the current operation is executed. DeleteLast is symmetric to DeleteFirst.

RetrieveFirst returns the first element of the list. The precondition of RetrieveFirst says that the list must be non-empty in order for this operation to make sense. The postcondition says that the result is indeed the first element, and that RetrieveFirst is a pure function (it does not mutate the state of the circular list). RetriveLast is symmetrical to RetrieveFirst.

What about the operations Empty, Full, CountElements, IsCircular, IsFirst, IsLast, RetrieveSecond, and RetrieveButLast? They are intended to be auxiliary, public boolean operations in the circular list. In an implementation of CircularList we must implement these operations. They are supposed to be implemented as simple as possible, and they are not supposed to carry preconditions and postconditions. In order to be operational (meaning that the specification can be confirmed at run-time) these auxiliary operations be must be implemented. Nothing comes for free! In reality, we check the consistency between the operations listed in Program 50.1 and the auxiliary boolean operations. An inconsistency reveals an error in either the circular list operations, or in the auxiliary operations. The necessary auxiliary operations are typically much simpler than the circular list operations, and therefore an inconsistency most often will reveal an error in the way we have implemented a circular list operation.

50.3.  An Assertion Language
Contents   Up Previous Next   Slide Annotated slide Aggregated slides    Subject index Program index Exercise index 

We are now about to focus on the language in which we formulate the assertions (preconditions and postconditions). In the previous section we have studied examples, in which we have met several features in the assertion language.

As it will appear, we are pragmatic with respect to the assertion language. The reason is that we allow programmed, boolean functions to be used in the assertion language. These boolean function are siblings to the functions that we are about to specify.

It is an important goal that the preconditions and the postconditions should be checkable at program execution time. Thus, the it should be possible and realistic to evaluation the assertions at run-time.

The following items characterize the assertions language:

Logical expressions - as in the programming language Programmed assertions - via boolean functions of the programming language Should be simple functions Problems if there are errors in these Universal ("for all...") and existential ("there exists...") quantifiers Requires programming - iteration - traversal It may be expensive to check assertions with quantifiers Informal assertions, written in natural language Cannot be checked Much better than nothing Special means of expression old Expr - The value of the expression at the beginning of the operation nochange - A simple way to state that the operation has not changed the state of the object

Use of universal and existential quantifiers, known from mathematical formalisms, makes it hard to check the assertions. Therefore such means of expressions do not exist directly in the assertion language. If we wish to express for all ... or there exists ... it must be programmed explicitly in boolean functions.

We may easily encounter elements of a specification that we cannot (or will no) check by programmed exceptions. It may be too expensive, or too complicated to program boolean functions which represent these elements. In such situations we may wish to fall back on informal assertions, similar to comments.