Recursion plays an important role for non-trivial functional programs. One of the reasons is that recursive data structures are used heavily in functional programs. Just take, as example, linear lists, cf. Chapter 6.

As another reason, most non-trivial needs some kinds of repeating structures - iteration. In our style of Scheme programming, we use recursive functions for iterative purposes. In this chapter we will see how this can be done without excessive use of memory resources.

And as before we attempt to illustrate also this topic with examples from the web domain.

11.1.  Recursion
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

In this section we characterize the basic ideas of recursion, and the kinds of problem solving which are aided by recursion.

We would like to refer the reader to an ECIU material on recursion, which in a more careful way discusses and illustrates the ideas [eciu-recursion]. Notice that there is some overlap with the ECIU material and the material you are reading now.

11.2.  List processing
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

We have already discussed lists as a recursive data type in Section 6.1. In this section we will give an extended LAML related example of recursive list processing in Scheme.

The function find-href-attribute in Program 11.1 extracts the href attribute value from an attribute property list. Property lists have already been discussed in Section 6.6.

Notice the recursive nature of the function find-href-attribute. The recursive call is highlighted with red color.

It happens to be the case that the function in Program 11.1 is tail recursive, cf. the discussion in Section 11.5.

1
2
3
4
5
6
7
8
9
10
11
12
13

; Return the href attribute value from a property list
; Return #f if no href attribute is found.
; Pre-condition: attr-p-list is a property list - 
; of even length.  
(define (find-href-attribute attr-p-list)
 (if (null? attr-p-list)
     #f
     (let ((attr-name (car attr-p-list))
           (attr-value (cadr attr-p-list))
           (attr-rest (cddr attr-p-list)))
      (if (eq? attr-name 'href)
          attr-value
          (find-href-attribute attr-rest)))))

To stay concrete, we show an example of using the function find-href-attribute in Program 11.2.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

1> (define a-clause 
    (a 'id "myid" 'class "myclass" 'href "http://www.cs.auc.dk"))

2> a-clause
(ast "a" () 
  (id "myid" class "myclass" href "http://www.cs.auc.dk" 
   shape "rect") 
  double xhtml10-strict)

3> (render a-clause)
"<a id = \"myid\" class = \"myclass\" 
    href = \"http://www.cs.auc.dk\"></a>"

4> (define attr-list (ast-attributes a-clause))

5> attr-list
(id "myid" class "myclass"
 href "http://www.cs.auc.dk" shape "rect")

6> (find-href-attribute attr-list)
"http://www.cs.auc.dk"  
>

11.3.  Tree processing (1)
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

Trees are another classical example of recursive data types.

In this section we show a web document and its internal structure. In Section 11.4 we show how to traverse this document, by means of tree traversal, with the purpose of extracting and collecting all URLs from href attributes of anchor elements in the document.

The LAML document in Program 11.3 shows a web document, in which we have highlighted all the anchor elements - the a elements. The tree structure in Figure 11.1 shows the hierarchical composition of the document, in terms of HTML elements. In the web version of the material - slide or annotated slide view - you can also access the actual abstract syntax tree - AST - which is the internal document representation of LAML. We do not include it in this version of the material because it is relatively long.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

(load (string-append laml-dir "laml.scm"))
(laml-style "simple-xhtml1.0-strict-validating")

(write-html '(prolog pp)
(html
 (head (title "Demo Links"))
 (body
  (p "ACM has a useful"
     (a 'href "http://www.acm.org/dl" "digital library") )
  (p "The following places are also of interest:")

  (ul
   (li (a 'href "http://www.ieee.org/ieeexplore/" "The IEEE"))
   (li "The" (a 'href "http://www.w3c.org" "W3C") "site")
   (li 
    (a 'href "http://link.springer.de/link/service/series/0558/" 
       "Lecture Notes in Computer Science")))

  (p "Kurt Nørmark" (br) 
     (a 'href "http://www.cs.auc.dk" "Dept. of Comp. Science") 
     (br)
     (a 'href "http://www.auc.dk" "Aalborg University")))))

(end-laml)

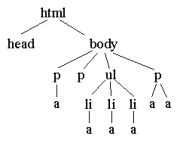
Figure 11.1    The syntax tree of the web document with the root made up by the html element.

11.4.  Tree processing (2)
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

We continue the example from Section 11.3 .

In Program 11.4 we show the function extract-links . The function is indirectly recursive via the function extract-links-ast-list .

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

; Return a list of URLS as located in the a elements of ast.  
(define (extract-links ast)
 (if (ast? ast)
     (let ((name (ast-element-name ast))
           (subtrees (ast-subtrees ast))
          )
       (if (equal? name "a")
           (let ((href-attr-value 
                  (find-href-attribute (ast-attributes ast))))
             (if href-attr-value (list href-attr-value) '()))
           (extract-links-ast-list subtrees)))
     '()))

; Return a list of URLS as located in the a elements of 
; the list of ast's as passed in ast-list.  
(define (extract-links-ast-list ast-list)
 (if (null? ast-list)
     '()
     (append 
      (extract-links (car ast-list))
      (extract-links-ast-list (cdr ast-list)))))

The extract-links function above traverses the internal AST structure of a web document. When an anchor element is encountered, when (equal? name "a") becomes true, we collect the href attribute by means of the function find-href-attribute, which we described in Section 11.2, see Program 11.1. In the cases where we do not encounter an anchor element, the call (extract-links-ast-list subtrees) causes traversal of the list of subtrees.

In the dialogue shown below we illustrate how to extract the URLs from a demo document, which we assume is identical with the document in Program 11.3.

1
2
3
4
5
6
7
8
9
10

1> (define doc-ast 
    (html
     (head (title "Demo Links"))
     (body
       ...)))

2 > (extract-links doc-ast)
("http://www.acm.org/dl" "http://www.ieee.org/ieeexplore/" "http://www.w3c.org"
 "http://link.springer.de/link/service/series/0558/" "http://www.cs.auc.dk"
 "http://www.auc.dk")

  (outline-copy '((a b c) (d e . f) (h i))) =>
     ((- - -) (- - . -) (- -))

11.5.  Recursion versus iteration
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

The purpose of this section is to introduce and not least motivate the idea of tail recursion.

A tail call is the last 'thing' to be done before the function returns. Therefore there is no need to maintain any activation record of such a recursive call - we can reuse the callers activation record.

The main source of insight to understand tail recursiveness is a series of images, which are available in the web version of the material (slide view). You should definitively consult this before you go on in this material.

11.6.  Example of recursion: number-interval
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

We provide an example of a recursive function, namely number-interval.

The version of number-interval shown in Program 11.6 is not tail recursive. The rewriting of the function in Program 11.7 is tail recursive however. Notice that the function in Program 11.7 needs a helping function, number-interval-iter-help, with an appropriate parameter profile.

1
2
3
4

(define (number-interval f t)
 (if (<= f t)
     (cons f (number-interval (+ f 1) t))
    '()))

1
2
3
4
5
6
7
8

(define (number-interval-iter f t)
  (reverse (number-interval-iter-help f t '())))


(define (number-interval-iter-help f t res)
  (if (<= f t)
      (number-interval-iter-help (+ f 1) t (cons f res))
      res))

We show below a couple of concrete applications of the functions in Program 11.6 and Program 11.7.

1
2
3
4
5
6
7
8

1> (number-interval 1 10)
(1 2 3 4 5 6 7 8 9 10)

2> (number-interval-iter 10 20)
(10 11 12 13 14 15 16 17 18 19 20)

3> (number-interval-iter 20 10)
()

  (define (my-append lst1 lst2)
       (cond ((null? lst1) lst2)
             (else (cons (car lst1) (my-append (cdr lst1) lst2)))))

  (define (my-next-append lst1 lst2)
    (my-next-append-1 lst1 lst2 ...))

  (define (my-next-append-1 lst1 lst2 res)
    (cond ((null? lst1) ...)
          (else (my-next-append-1 (cdr lst1) lst2 ...))))

        (replicate-to-length '(a b c) 8) =>
        (a b c a b c a b)

        (replicate-to-length '(a b c) 2) =>
        (a b)
      

11.7.  Examples of recursion: string-merge
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

This section and the next give yet other examples of recursive functions. We start with string-merge.

1
2
3
4
5
6

(define (string-merge str-list-1 str-list-2)
 (cond ((null? str-list-1) (apply string-append str-list-2))
       ((null? str-list-2) (apply string-append str-list-1))
       (else (string-append
              (car str-list-1) (car str-list-2)
              (string-merge (cdr str-list-1) (cdr str-list-2))))))

The function in Program 11.9 not tail recursive. To remedy this weakness, we make another version which is. It is shown in Program 11.10.

As it is characteristic for all tail recursive functions, the state of the iteration needs to be represented in the parameter list, here in the helping function called merge-iter-helper. The necessary state for string merging purpose is reduced to the resulting, merged string - the res parameter.

1
2
3
4
5
6
7
8
9
10
11
12
13

(define (string-merge-iter str-list-1 str-list-2)
 (merge-iter-helper  str-list-1 str-list-2 ""))

(define (merge-iter-helper str-list-1 str-list-2 res)
 (cond ((null? str-list-1) 
          (string-append res (apply string-append str-list-2)))
       ((null? str-list-2) 
          (string-append res (apply string-append str-list-1)))
       (else (merge-iter-helper
                (cdr str-list-1) 
                (cdr str-list-2)
                (string-append 
                    res (car str-list-1) (car str-list-2))))))

In the LAML software, the function string-merge is used in several contexts. One of them is in the function list-to-string , which we show in Program 11.11 We could in fact have applied list-to-string in the function as-string, which we discussed in Program 10.4.

1

11.8.  Examples with recursion: string-of-char-list?
Contents   Up Previous Next   Slide    Subject index Program index Exercise index 

The last example in this chapter is a boolean function that can check if a string is formed by the characters from a given alphabet.

1
2
3
4
5
6
7
8

(define (string-of-char-list? str char-list)
  (string-of-char-list-1? str char-list 0 (string-length str)))

(define (string-of-char-list-1? str char-list i lgt)
  (if (= i lgt)
      #t
      (and (memv (string-ref str i) char-list)
           (string-of-char-list-1? str char-list (+ i 1) lgt))))

The predicates blank-string? and numeric-string? in Program 11.13 are very useful for many practical purposes. The first function checks if a string represents white space only. The latter function checks if a string represents a decimal integer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

;; A list of characters considered as blank space characters
(define white-space-char-list
   (list #\space (as-char 13) (as-char 10) #\tab))

;; Is the string str empty or blank (consists of white space)
(define (blank-string? str)
  (or (empty-string? str) 
      (string-of-char-list? str white-space-char-list)))

;; Returns if the string str is numeric.
;; More specifically, does str consist exclusively of the
;; ciffers 0 through 9. 
(define (numeric-string? str)
  (string-of-char-list? str 
    (list #\0 #\1 #\2 #\3 #\4 #\5 #\6 #\7 #\8 #\9 )))

        (front-sublist '(a b c d e) 3)  =>
        (a b c)
      
        (front-sublist '(a b c d e) 6)  =>
        ERROR

        (sublists '(a b c d e f) 3) =>
        ((a b c) (d e f))

         <table>
           <tr> <td>a</td> <td>b</td> <td>c</td> </tr>
           <tr> <td>d</td> <td>e</td> <td>f</td> </tr>
         </table>