


   | Object-oriented programming in Scheme |
In Section 8.5 we have described function-objects, which are returned when we evaluate lambda expressions. Function objects are also called closures, because a function object captures and 'closes around' the free name, on which the function object depends (due to the use of static binding of free names).
In this section we will see how to combine function objects to represent objects, in the sense of the object-oriented programming paradigm.
29.1. Functions with private context
Contents Up Previous Next Slide Subject index Program index Exercise index
We start gently with some observations about private context around functions. It turns out later that this is one of the key ideas when we want to represent objects by means of functions. The insight in this section shows how to arrange some private, encapsulated state around a function. This is relevant because the idea of encapsulation is central in the object-oriented paradigm.
It is possible to define a private context around a function |
The function below is defined in a private context. The let construct sets up a number of names (not shown directly in the program), which can be accessed from the lambda expression. Moreover, no other places than the lambda expression can access these names. Therefore the context is private to the shown lambda expression.
1 2 3 4 | (define function-with-private-context
(let (CONTEXT)
(lambda (PARAMETERS)
BODY))) | |||
|
Before we proceed with a deeper understanding and exploration of private context around functions, we will give a concrete example in Table 29.1 below. We take one of our favorite examples, namely the use of the HTML mirror functions html, head, body, etc, to define a document function. The document function has a private context, in which we redefine html and body . The redefinition binds a couple of relevant attributes, by use of the function modify-element, which we introduced in Section 18.5.
| Expression | Value |
(define document
(let
((html
(xml-modify-element html
'xmlns "http://www.w3.org/1999/xhtml"))
(body
(xml-modify-element body
'bgcolor (rgb-color-encoding 255 0 0)))
)
(lambda (ttl bdy)
(html
(head (title ttl))
(body bdy))))) | |
(document "A title" "A body") | <html xmlns =
"http://www.w3.org/1999/xhtml">
<head>
<title>A title</title>
</head>
<body bgcolor = "#ff0000">
A body
</body>
</html> |
| Table 29.1 An example in which we abstract a (html (head (title..)) (body ...)) expression in a lambda expression, of which we define a private context. The context redefines the html and body functions to 'specialized' versions, with certain attributes. Notice the importance of the 'simultaneous name bindings' of let in the example (as explained in an earlier lecture). Also notice that we have discussed the modify-element higher-order function before. |
Now we know how to deal with private context around a function. In the next section we will use this knowledge to approach the definition of classes, as known from the object-oriented programming paradigm.
29.2. Classes and objects
Contents Up Previous Next Slide Subject index Program index Exercise index
We will now demonstrate that a function definition can be interpreted as a class, and that a function call can play the role of an object. In other words, certain lambda expressions will be regarded as classes, and certain closures will be seen as objects.
Due to (1) the first class status of functions, and due to (2) the use of static binding of free names, it is possible to interpret a closure as an object With this interpretation, it is possible to regard certain function definitions as classes |
In Program 29.2 we see the definition of Point, which we want to play the role of a class. The purple lambda expression, the value of which is returned from Point, is the object handle, which represents the object. Notice that this object handle really is a dispatcher, which returns one of the red methods given a message parameter as input. Thus, the object handle manages method lookup in the object. The letrec construct organizes the methods, which all are defined inside the scope of the green instance variables, which are just the 'construction parameters' of the point.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | (define (point x y)
(letrec ((getx (lambda () x))
(gety (lambda () y))
(add (lambda (p)
(point
(+ x (send 'getx p))
(+ y (send 'gety p)))))
(type-of (lambda () 'point))
)
(lambda (message)
(cond ((eq? message 'getx) getx)
((eq? message 'gety) gety)
((eq? message 'add) add)
((eq? message 'type-of) type-of)
(else (error "Message not understood")))))) | |||
|
In the add method we use the send function. The send function sends a message to an object. We show the definition of the send function in Program 29.3. The send function just looks up the method, after which it calls the method by means of apply.
1 2 3 | (define (send message obj . par)
(let ((method (obj message)))
(apply method par))) | |||
|
The send function is of course of interest also outside the classes. Whenever we need to communicate with an object, we do it by use of the send function. We will encounter send and other similar functions in the following sections.
On the practical side, it might be a good idea to rename send , for instance to send-message . It is likely that send already is the name of a function in your Scheme system. In DrScheme and MzScheme this is indeed the case. So in order to avoid problems with this, you can consider a systematic renaming when you are playing with the Point class in Exercise 8.1.
The purpose of this exercise is to strengthen your understanding of functions used as classes in Scheme.
First, play with the existing Point class defined on this page available from the on-line version of this material.
As an example, construct two points and add them together. Also, construct two lists of each four points, and add them together pair by pair.
Define a new method in the Point class called (move dx dy) , which displaces a point with dx units in the x direction and dy units in the y direction. We encourage you to make a functional solution in which move creates a new displaced point. After that you can make an imperative solution in which the state of the receiving point is changed.
Finally, define a new class, Rectangle , which aggregates two points to a representation of a rectangle. Define move and area methods in the new class.
As a practical remark to the 'class Point ' and the send primitive, be sure to define send before you define Point . (This is done to redefine an existing send procedure in MzScheme).
Solution
29.3. A general pattern of classes
Contents Up Previous Next Slide Subject index Program index Exercise index
We will now generalize the ideas exemplified in the Point class above. With this we will discuss a general pattern for simulation of classes and objects in Scheme.
If you want additional information about the simulation of object-oriented concepts in Scheme you can consult [Normark90a].
The following shows a template of a function that serves as a class |
In the program below pattern of a class is shown. As explained in Program 29.4 there are construction parameters, instance variables, methods, and the self function. The methods and the self function are defined through explicit define forms. This is just syntactic sugar, instead of using letrec as in Point - see Program 29.2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | (define (class-name construction-parameters)
(let ((instance-var init-value)
...)
(define (method parameter-list)
method-body)
...
(define (self message)
(cond ((eqv? message selector) method)
...
(else (error "Undefined message" message))))
self)) | |||
|
Below we show the send function, which we also saw in Program 29.3. The version in Program 29.5 includes a little error handling in addition to method lookup and method activation. The program also contains a syntactic sugaring function called new-instance , which just 'calls the class' with the purpose of class instantiation.
1 2 3 4 5 6 7 | (define (new-instance class . parameters)
(apply class parameters))
(define (send message object . args)
(let ((method (object message)))
(cond ((procedure? method) (apply method args))
(else (error "Error in method lookup " method))))) | |||
|
29.4. Example of the general class pattern
Contents Up Previous Next Slide Subject index Program index Exercise index
Let us now take a look at the Point class, programmed with the class pattern introduced in Section 29.3 . We carefully introduce instance variables x and y, even though they are not strictly needed. The construction parameters of Point - also called x and y - are sufficient to represent the object state.
The Point class redefined to comply with the general class pattern |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | (define (point x y)
(let ((x x)
(y y)
)
(define (getx) x)
(define (gety) y)
(define (add p)
(point
(+ x (send 'getx p))
(+ y (send 'gety p))))
(define (type-of) 'point)
(define (self message)
(cond ((eqv? message 'getx) getx)
((eqv? message 'gety) gety)
((eqv? message 'add) add)
((eqv? message 'type-of) type-of)
(else (error "Undefined message" message))))
self)) | |||
|
Below, in Program 29.7 we show a scenario in which we create two points, and bind them to the variables p and q. The sum of p and q is bound to the variable named p+q . We also send getx and gety messages to the points in order to assure, that they are located as expected.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 1> (define p (new-instance point 2 3)) 2> (send 'getx p) 2 3> (define q (new-instance point 4 5)) 4> (define p+q (send 'add p q)) 5> (send 'getx p+q) 6 6> (send 'gety p+q) 8 | |||
|
29.5. A general pattern of classes with inheritance
Contents Up Previous Next Slide Subject index Program index Exercise index
Now that we have seen how the simple aspects of object-oriented programming can be simulated in Scheme, we will move on to a slightly more advanced aspect, namely inheritance. We will see that it is possible to organize object parts in such a way that they can be considered as an object of a class, which inherits from another class.
In Program 29.8 the binding of super to new a 'super part' (the red program fragment) is the place to look first. At this location we instantiate the super part of the current object. In the dispatcher - earlier called self - we carry out method lookup in super , in case we do not find the method in the current object part. This is in reality the operational manifestation of inheritance (from subclass part to super part - and not as usually conceived, the other way around).
You should already now take a look at the left (green) part of Figure 29.1 to understand the super chain of the object. The self variable in the figure holds the value of dispatch. Thus, self refers to the object handle.
The following shows a template of a function that serves as a subclass of another class |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | (define (class-name parameters)
(let ((super (new-part super-class-name some-parameters))
(self 'nil))
(let ((instance-variable init-value)
...)
(define (method parameter-list)
method-body)
...
(define (dispatch message)
(cond ((eqv? message 'selector) method)
...
(else (method-lookup super message))))
(set! self dispatch))
self)) | |||
|
When object parts refer to each other in a chain of super variables, the top object part is deemed to be special. As usual, the most general class is called Object. It is shown in Program 29.9. The super reference is 'empty' (the empty list), and the dispatch function ends the method lookup at this point.
1 2 3 4 5 6 7 8 9 | (define (object)
(let ((super '())
(self 'nil))
(define (dispatch message)
'())
(set! self dispatch)
self)) | |||
|
Below, in Program 29.10, the syntactic sugaring functions new-instance , new-part , send , and method-lookup are shown. The function new-part is used to make a new part object, whereas new-instance is used to make a whole object. Currently they are identical, but later we will make a small difference in between them. In reality method-lookup and send have survived from Section 29.3. Only some additional error handling has been added.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | (define (new-instance class . parameters)
(apply class parameters))
(define (new-part class . parameters)
(apply class parameters))
(define (method-lookup object selector)
(cond ((procedure? object) (object selector))
(else
(error "Inappropriate object in method-lookup: "
object))))
(define (send message object . args)
(let ((method (method-lookup object message)))
(cond ((procedure? method) (apply method args))
((null? method)
(error "Message not understood: " message))
(else
(error "Inappropriate result of method lookup: "
method))))) | |||
|
29.6. An example of classes with inheritance
Contents Up Previous Next Slide Subject index Program index Exercise index
We will of course take a look at a concrete example with class inheritance. Below we define a heir of Point . For the sake of the example, we could also have extended Point with a third dimension, but we choose the somewhat foolish specialization called ColorPoint .
If you want to play with the class, you can access all the necessary stuff - including the superclass Point - from the slide or annotated slide view of this material.
We sketch one of the favorite toy specializations of Point - ColorPoint |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | (define (color-point x y color)
(let ((super (new-part point x y))
(self 'nil))
(let ((color color))
(define (get-color)
color)
(define (type-of) 'color-point)
(define (dispatch message)
(cond ((eqv? message 'get-color) get-color)
((eqv? message 'type-of) type-of)
(else (method-lookup super message))))
(set! self dispatch))
self)) | |||
|
We also include a sample dialogue with color points, see Program 29.12. Of course, it is best for you to play with the classes yourself.
Adding two color points together creates a point, not a color point. In Exercise 8.2 we explore this problem.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | 1> (define cp (new-instance color-point 5 6 'red)) 2> (send 'get-color cp) red 3> (send 'getx cp) 5 4> (send 'gety cp) 6 5> (define cp-1 (send 'add cp (new-instance color-point 1 2 'green))) 6> (send 'getx cp-1) 6 7> (send 'gety cp-1) 8 8> (send 'get-color cp-1) Undefined message get-color 9> (send 'type-of cp-1) point | |||
|
On this page we have introduced the class ColorPoint, which inherits from Color .
In the sample dialogue with a couple of color points we have identified the problem that the sum of two color points is not a color point. Why is it so?
You are now supposed to make a few changes in the classes Point and ColorPoint. In order to make it realistic for you to play with the classes, your starting point is supposed to be a pre-existing file, with all the useful stuff (available from the on-line version of this material).
When you experiment with points and color-points, use M-x run-laml-interactively from Emacs.
29.7. The interpretation of self
Contents Up Previous Next Slide Subject index Program index Exercise index
The simulation of inheritance involves an aggregation of object parts to a holistic object. In order to tie the whole object together, self (the object handle) of all parts must point to the most specialized object part.
In Figure 29.1 we show what we want to achieve. The green hierarchy to the left shows the situation until now, where self at each level points to the current object part. The yellow hierarchy to the right shows the situation we want to establish.
In order to obtain virtual methods of classes we need another interpretation of self |
The interpretation of self can be related to virtual methods in the object-oriented paradigm. A method is virtual if the type of the receiving object, rather the type of the qualifying class, determines the method binding in a method lookup process.
Thus, from an arbitrary object part, we want to be able to access the most specialized interpretation of a method. In order to provide for this, self must give access to the most specialized object part. Without this, there is no way at all to access the 'top object part' from a 'non-top object part'.
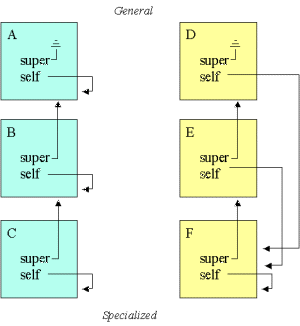
| Figure 29.1 Two different interpretations of self . We see two linear class hierarchies. The class C inherits from B, which in turn inherits from A. And similarly, F inherits from E, which inherits from D. The one to the left - in the green class hierarchy - is the naive one we have obtained in our templates and examples until now. The one to the right - in the yellow class hierarchy, shows another interpretation of self . Following this interpretation, self at all levels refer to the most specialized object part. |
29.8. A demo of virtual methods
Contents Up Previous Next Slide Subject index Program index Exercise index
It is now time to show the effect of virtual methods. In Program 29.13 we define a class x which is the superclass of a class y in Program 29.14. Thus, y inherits from x . In both of the classes we see an extra bookkeeping method set-self! , which is responsible for mutating self to the proper object part. Notice that set-self! is not of interest to the programmers, who use the x and y classes. The set-self! methods are internal affairs of the classes.
On this page we will make two artificial classes with the purpose of demonstrating virtual methods |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | (define (x)
(let ((super (new-part object))
(self 'nil))
(let ((x-state 1)
)
(define (get-state) x-state)
(define (res)
(send 'get-state self))
(define (set-self! object-part)
(set! self object-part)
(send 'set-self! super object-part))
(define (self message)
(cond ((eqv? message 'get-state) get-state)
((eqv? message 'res) res)
((eqv? message 'set-self!) set-self!)
(else (method-lookup super message))))
self))) ; end x | |||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | (define (y)
(let ((super (new-part x))
(self 'nil))
(let ((y-state 2)
)
(define (get-state) y-state)
(define (set-self! object-part)
(set! self object-part)
(send 'set-self! super object-part))
(define (self message)
(cond ((eqv? message 'get-state) get-state)
((eqv? message 'set-self!) set-self!)
(else (method-lookup super message))))
self))) ; end y | |||
|
The dialogue in Program 29.15 is a minimal example that illustrates the effect of the new interpretation of self . Sending the res message to the y-object b gives the value 2, which shows that the get-state of y (not the get-state of x ) is called by the res method. Notice that the res method is inherited from x to y .
1 2 3 4 5 6 7 8 9 | 1> (define a (new-instance x)) 2> (define b (new-instance y)) 3> (send 'res a) 1 4> (send 'res b) 2 | |||
|
The program below, Program 29.16, shows the new-instance function, which - in a declarative fashion - asks for virtual operations. The function virtual-operations , sends the set-self! method to the object, which in turn will activate the set-self! methods at all levels in the object. This causes the adjustment of self , as illustrated in the right part of Figure 29.1.
1 2 3 4 5 6 7 8 | (define (new-instance class . parameters) (let ((instance (apply class parameters))) (virtual-operations instance) instance)) ; Arrange for virtual operations in object (define (virtual-operations object) (send 'set-self! object object)) | |||
|
This is an open exercise - maybe the start of a minor project.
In the original mirror of HTML in Scheme, the HTML mirror functions, return strings. In the current version, the mirror functions return an internal syntax tree representation of the web documents. With this, it is realistic to validate a document against a grammar while it is constructed. In this exercise we will experiment with an object representation of a web document. We will use the class and object representation which we have introduced in this lecture.
Construct a general class html-element which implement the general properties of a HTML element object. These include:
In addition, construct one or more examples of specific subclasses of html-element , such as html , head , or body. These subclasses should have methods to access particular, required constituents of an element instance, such as the head and the body of a HTML element, and title of a head element. Also, the concrete validation predicate must be redefined for each specific element.
There is no solution to this exercise
29.9. References
| [Oop-sim] | Simulation of object-oriented mechanisms in Scheme - A technical report http://people.cs.aau.dk/~normark/pp-*/oop-scheme.pdf |
| [Normark90a] | Kurt NÝrmark, "Simulation of Object-oriented Concepts and Mechanisms in Scheme", Tech Report no. R 90-01, Department of Mathematics and Computer Science, Institute of Electronic Systems, Aalborg University, January 1990. |