
Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark
| Abstract Previous lecture Next lecture Index References Contents | In this lecture we will explore the higher-order functions, both on classical ground and with examples from the WWW domain. |
| Recursion and Iteration |
| Program: The forms discussed. |
|
| Recursion Slide Annotated slide Contents Index References |
|
| The concept recursion: Recursion is an algorithmic program solving idea that involves solution of subproblems of the same nature as the overall problem |
The problem solving technique sketched here is called divide and conquer. It is not all divide and conquer problems that involve recursion. But many do in fact. Recursion comes into play when the subproblems P1 ... Pn turn out to be of the same nature as the overall problem, and as such they can be solved by the same 'medicine' as used for the overall problem P. |
|
| Recursion versus iteration Slide Annotated slide Contents Index References |
|
| The concept tail recursion: Tail recursion is a variant of recursion in which the recursive call takes place without contextual, surrounding calculations in the recursive function. In a tail recursion function the recursive call is a tail call (see next slide) | A tail call is the last 'thing' to be done before the function returns. Therefore there is no need to maintain any activation record of such a call - we can reuse the previous activation record. The image series below will illustrate this. |
| Image series: A recursive formulation of the function fak and the accompanying recursive process | A recursive formulation of the function fak and the accompanying recursive process |
| Image no. 1. The recursion is developed - activation records are stacked |  |
| Image no. 2. The recursion is developed - activation records are stacked |  |
| Image no. 3. The recursion is developed - activation records are stacked |  |
| Image no. 4. The recursion is developed - activation records are stacked |  |
| Image no. 5. The turning point is reached - now on to actual multiplication |  |
| Image no. 6. Trivial multiplication with 1 | 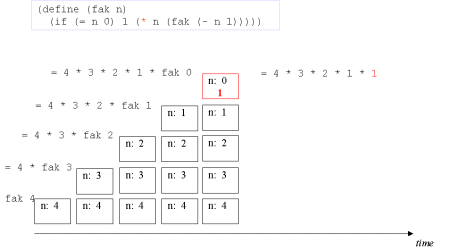 |
| Image no. 7. Yet another time | 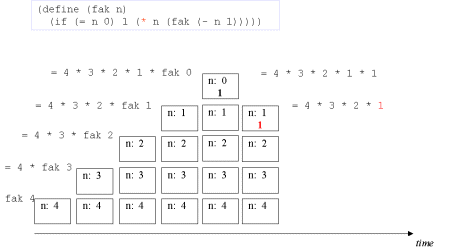 |
| Image no. 8. Multiplication with 2 |  |
| Image no. 9. Multiplication with 3 |  |
| Image no. 10. Multiplication with 4 |  |
| Image series: A tail recursive formulation of the function fak and the accompanying iterative process without memory optimization | A tail recursive formulation of the function fak and the accompanying iterative process without memory optimization |
| Image no. 1. The recursion develops - multiplication with 4 |  |
| Image no. 2. The recursion develops - multiplication with 3 |  |
| Image no. 3. The recursion develops - multiplication with 2 |  |
| Image no. 4. The recursion develops - multiplication with 1 |  |
| Image no. 5. Turning point - we have the result in r |  |
| Image no. 6. Non-productive unstacking |  |
| Image no. 7. Non-productive unstacking |  |
| Image no. 8. Non-productive unstacking |  |
| Image no. 9. Non-productive unstacking |  |
| Image no. 10. Non-productive unstacking |  |
| Image series: A tail recursive formulation of the function fak and the accompanying, memory optimized iterative process | A tail recursive formulation of the function fak and the accompanying, memory optimized iterative process |
| Image no. 1. Multiplication with 4 |  |
| Image no. 2. Multiplication with 3 - frame reused |  |
| Image no. 3. Multiplication with 2 - frame reused |  |
| Image no. 4. Multiplication with 1 - frame reused |  |
| Image no. 5. Done - the result is in r |  |
|
| Tail Calls Slide Annotated slide Contents Index References |
|
| Program: Tail call. |
|
| Program: Example of tail calls and non tail calls. |
|
|
| Example of recursion: number-interval Slide Annotated slide Contents Index References |
|
| Program: The function number-interval from the general LAML library. This function returns a list of t-f+1 numbers from f to t .Try it out!. |
|
| Program: The function number-interval-iter is an iterative, tail recursive variant of number-interval. |
|
| Program: A sample dialogue with the number interval functions. |
|
| Exercise 2.3. The append function | The function append, which is a standard Scheme function, concatenates two or more lists. Let us here show a version which appends two lists: (define (my-append lst1 lst2)
(cond ((null? lst1) lst2)
(else (cons (car lst1) (my-append (cdr lst1) lst2))))) We will now challenge ourselves by programming an iterative solution, by means of tail recursion. We start with the standard setup: (define (my-next-append lst1 lst2)
(my-next-append-1 lst1 lst2 ...)) where my-next-append-1 is going to be the tail recursive function: (define (my-next-append-1 lst1 lst2 res)
(cond ((null? lst1) ...)
(else (my-next-append-1 (cdr lst1) lst2 ...)))) Fill out the details, and try out your solution. You may encounter a couple of problems! Do your best to work around these problems, maybe by changing aspects of the templates I have given above. |
| Exercise 2.3. A list replication function | Write a tail recursive function called replicate-to-length, which in a cyclic way (if necessary) replicates the elements in a list until the resulting list is of a certain exact length. You should think of replicate-to-length as a function that iterates over the elements of the list, repeatedly, if necessary. You will probably need to write a helping function to replicate-to-length, which is tail recursive. The following serves as an example:
(replicate-to-length '(a b c) 8) =>
(a b c a b c a b)
(replicate-to-length '(a b c) 2) =>
(a b)
In other words, in (replicate-to-length lst n), take elements out of lst, cyclic if necessary, until you reach n elements. |
| Examples of recursion: string-merge Slide Annotated slide Contents Index References |
|
| Program: The recursive function string-merge. Notice that this function is a general recursive function.
The recursive call, emphasized above, is not in a tail position, because of the embedding in string-append. |
|
| Program: A tail recursive version of string-merge. |
|
| Exercise 2.4. More about string-merge | We have seen two variants of string-merge on the accompanying slide. Both make use of (apply string-merge ...) in the cases where one of the lists become empty. apply calls a function on a list of parameters. Thus (apply + (list 1 2)) is equivalent to (+ 1 2). Eliminate the use of apply, such that string-merge (tail) recursively builds the end of the list by a number of calls to string-append (one for each element in the non-empty list). |
| Examples with recursion: string-of-char-list? Slide Annotated slide Contents Index References |
|
| Program: The function string-of-char-list? which relies on the tail recursive function string-of-char-list-1?.
The function string-of-char-list-1? iterates through the characters in str, via the controlling parameters i and lst. |
|
| Program: Applications of string-of-char-list?. The function blank-string? determines if a string is formed entirely of white space characters.
The function numeric-string? is a predicate that returns true if the string consists exclusively of decimal digits. This is, for instance,
useful to check the form input of dates and time in some server-based web applications. The version of numeric-string? in the lib/general.scm
of LAML is slightly more general than the version shown above (it allows + or - signs as well, depending on an optional parameter). |
|
| Exercises Slide Annotated slide Contents Index References |
|
| Exercise 2.7. Sublists of a list | The first part of this exercise is similar to an exercise from the previous lecture. In this exercise we will program a function front-sublist which returns the first n elements of a list. The signature (the head) of the function should be (front-sublist lst n) where lst is a list and n is a number. As a precondition it can be assumed that lst is a proper list and that n is a non-negative integer. As a postcondition we want to guarantee that the length of the result is n. As an example
(front-sublist '(a b c d e) 3) =>
(a b c)
(front-sublist '(a b c d e) 6) =>
ERROR First, identify the extreme, border cases and be sure that you know how to handle these. Next, program the function with due respect to both the precondition and the postcondition. Next, test the function carefully in a dialogue with your Scheme system. Given the function front-sublist we will program the function sublists, which breaks a proper list into a list of sublists of some given size. As an example
(sublists '(a b c d e f) 3) =>
((a b c) (d e f)) Program the function sublists with use of front-sublist. Be careful to prepare you solution by recursive thinking. It means that you should be able to break the overall problem into a smaller problem of the same nature, as the original problem. You should feel free to formulate both preconditions and postconditions of the function sublists, such that the existing function front-sublist fits well. Hint: The Scheme function list-tail is probably useful when you program the function sublists. |
| Exercise 2.7. A variant of number-interval | We have studied the function number-interval in this lecture (on this slide) and we have seen that (number-interval 10 1) evaluates to the empty list. Program a variant of number-interval such that (number-interval 10 1) evaluates to the list (10 9 8 7 6 5 4 3 2 1). |
| Exercise 2.7. A variant of string-of-char-list? | The function string-of-char-list? was programmed with use of a help function which we called string-of-char-list-1? on this slide. The help function was programmed side by side with string-of-char-list?. As an altertive, string-of-char-list-1? could be programmed as a local function of string-of-char-list? Please do that, using an appropriate name binding form. The help function keeps track of an index i in an additional parameter. It is possible to program string-of-char-list? without use of a help function. This function should iterate over shorter and shorter text strings. Please do that now. Consider the efficiency of this function and our original version of string-of-char-list?. (The function substring is useful). |
| Recursion without define and letrec |
| The Challenge Slide Annotated slide Contents Index References |
|
| Program: A naive attempt to define a recursive function. |
|
| Program: Equivalent to the program above. |
|
| Program: A definition of fac with letrec. |
|
| Program: Equivalent to the program above - notice the use of assignment. |
|
| Program: Passing fac to itself - the key to a solution. |
|
|
| Development of the Y-combinator Slide Annotated slide Contents Index References |
|
|
| Program: Wishful thinking - the goal of our work: Generating a recursive factorial function from an almost recursive factorial function. |
|
| Program: The starting point - again. |
|
| Program: After simple currying. |
|
| Program: Abstracting (f f) out of if. |
|
| Program: After a simple renaming of fac to i. |
|
| Program: Introducing n as parameter to (lambda (h) ...). |
|
| Program: After currying. |
|
| Program: The lambda expression bound to g has been moved out. |
|
| Program: Empty let removed. |
|
| Program: Introduce function for (let ((i ..)) ...). |
|
| Program: A small but irritating detail. Get 5 out the self application stuff. |
|
| Program: Factoring self application stuff out. Call it Y. |
|
| Program: The end result. |
|
| Introduction to higher-order functions |
| Higher-order functions Slide Annotated slide Contents Index References | The idea of higher-order functions is of central importance for the functional programming paradigm. As we shall see on this and the following pages, this stems from the fact that higher-order functions can be further generalized by accepting functions as parameters. In addition, higher-order functions may act as function generators, because they allow functions to be returned as the result from other functions. |
| The concept higher-order function: A higher-order function accepts functions as arguments and/or is able to return a function as its result | ||
| The concept higher-order language: A higher-order language supports higher-order functions and allows functions to be constituents of data structures |
Order 0 data have nothing to do with functions. Numbers, lists, and characters are example of such data. Data of order 1 are functions which work on 'ordinary' order 0 data. Thus order 1 data are the functions we have been concerned with until now. Data of order 2 - and higher - are example of the functions that have our interest in this lecture. |
|
| Some simple and general higher-order functions Slide Annotated slide Contents Index References | It is time to look at some examples of higher-order functions. We start with a number of simple ones. |
|
| Program: The function flip changes the order of it's parameters. The function takes a function of two parameters, and returns another
function of two parameters. The only difference between the input and output function of flip is the ordering of their parameters. |
|
| Program: An alternative formulation of flip without use of the sugared define syntax. For easy comparison we show the original version below the alternative formulation.
The two different syntaxes are discussed in an earlier lecture, cf. the cross references. |
|
| Program: The function negate negates a predicate. Thus, negate takes a predicate function (boolean function) as parameter and
returns the negated predicate.
The resulting negated predicate returns true whenever the input predicate returns false, and vise versa. |
|
| Program: The function compose composes two functions which both are assumed to take a single argument. The resulting function composed of f and g returns f(g(x)), or in Lisp (f (g x)), given the input x .
The compose function from the general LAML library accepts two or more parameters, and as such it
is more general than the compose function shown here. |
|
| Exercise 2.8. Using flip, negate, and compose | Define and play with the functions flip, negate, and compose, as they are defined on this page . Define, for instance, a flipped cons function and a flipped minus function. Define the function odd? in terms of even? and negate. Be sure you understand your results. |
|
| Linear search in lists Slide Annotated slide Contents Index References |
|
| Program: A linear list search function. A predicate accepts as input an element in the list, and it returns either true (#t) or false (#f).
If the predicate holds (if it returns true), we have found what we searched for.
The predicate pred is passed as the first parameter to find-in-list. As it is emphasized in blue color, the predicate is
applied on the elements of the list. The first successful application (an application with true result) terminates the search,
and the element is returned. If the first case in the conditional succeeds (the brown condition) we have visited all elements in the list,
and we conclude that the element looked for is not there. In that case we return false. |
|
| Program: A sample interaction using find-in-list. We define a simple association list which relates persons (symbols) and
hair colors (strings). The third interaction searches for per's entry in the list. The fourth interaction
searches for a person with pink hair color. In the fifth interaction nothing is found, because no person has yellow hair color.
In the sixth interaction we illustrate the convenience of boolean convention in Scheme: everything but
#f counts as true. From a traditional typing point of view the let expression is problematic, because it
can return either a person (a symbol) or a boolean value. Notice however, from a pragmatic point of view,
how useful this is.
|
|
| Exercise 2.13. Linear string search | Lists in Scheme are linear linked structures, which makes it necessary to apply linear search techniques. Strings are also linear structures, but based on arrays instead of lists. Thus, strings can be linearly searched, but it is also possible to access strings randomly, and more efficiently. First, design a function which searches a string linearly, in the same way as find-in-list. Will you just replicate the parameters from find-in-list, or will you prefer something different? Next program your function in Scheme. |
| Exercise 2.13. Index in list | It is sometimes useful to know where in a list a certain element occurs, if it occurs at all. Program the function index-in-list-by-predicate which searches for a given element. The comparison between the given element and the elements in the list is controlled by a comparison parameter to index-in-list-by-predicate. The function should return the list position of the match (first element is number 0), or #f if no match is found. Some examples will help us understand the function:
(index-in-list-by-predicate '(a b c c b a) 'c eq?) => 2
(index-in-list-by-predicate '(a b c c b a) 'x eq?) => #f
(index-in-list-by-predicate '(two 2 "two") 2
(lambda (x y) (and (number? x) (number? y) (= x y)))) => 1
Be aware if your function is tail recursive. |
| Exercise 2.13. Binary search in sorted vectors | Linear search, as illustrated by other exercises, is not efficient. It is often attractive to organize data in a sorted vector, and to do binary search in the vector. This exercise is meant to illustrate a real-life higher-order function, generalized with several parameters that are functions themselves. Program a function binary-search-in-vector, with the following signature: (binary-search-in-vector v el sel el-eq? el-leq?) v is the sorted vector. el is the element to search for. If v-el is an element in the vector, the actual comparison is done between el and (sel v-el). Thus, the function sel is used as a selector on vector elements. Equality between elements is done by the el-eq? function. Thus, (el-eq? (sel x) (sel y)) makes sense on elements x and y in the vector. The ordering of elements in the vector is defined by the el-leq? function. (el-leq? (sel x) (sel y)) makes sense on elements x and y in the vector. The call (binary-search-in-vector v el sel el-eq? el-leq?) searches the vector via binary search and it returns an element el-v from the vector which satisfies (el-eq? (sel el-v) el). If no such element can be located, it returns #f. Here are some examples, with elements being cons pairs: (binary-search-in-vector '#( (2 . x) (4 . y) (5 . z) (7 . i) (9 . c) (11 . c)) 7 car = <=) => (7 . i) (binary-search-in-vector '#( (2 . x) (4 . y) (5 . z) (7 . i) (9 . c) (11 . c)) 2 car = <=) => (2 . x) (binary-search-in-vector '#( (2 . x) (4 . y) (5 . z) (7 . i) (9 . c) (11 . c)) 10 car = <=) => #f Be sure to program a tail recursive solution. |
| Exercise 2.13. Generating a C-style compare function | A C-style compare function (cmp x y) returns -1 if x is less than y, 0 if x is equal to y, and 1 if x is greater than y. Write a higher-order function make-comparator, that takes two functions lt (less than) and gt (greater than) as parameters and generates a C-style compare function. With a little more thought we can generate a C-style compare function from only the function lt. Give it a try. Use make-comparator and a standard function string<? to generate a function that compares two strings in a C-style (a Scheme version of strcmp). The other way around, write a higher-order function that takes a C-style compare function and generates a list of functions: lt, equal, gt. Test each of the three generated functions and make sure they work as expected. |
| Exercise 2.13. Higher-order functions in 'Functional Programming Languages' | A number of short papers appeared in 1996 in the journal Computing Surveys (as part of the 50 years celebration of the ACM) - among them a paper titled 'Functional Programming Languages' by Benjamin Goldberg. Take a brief look at the paper - in particular the section about 'Higher-order functions'. It is an easy paper to read. Rewrite the functions prod, fac, and power in Scheme, and give them a try. Do you get the results you would expect? If not, carry out the necessary corrections. The product operator is introduced to improve the recursive factorial function, suposedly in the direction of iteration. However, the paper is not successful in that respect. Why? Write an iterative, memory efficient, tail-recursive version of prod in Scheme. |
| Generation of list selectors Slide Annotated slide Contents Index References |
|
| Program: A simple version of the make-selector-function function. |
|
| Program: The existing LAML make-selector-function. It is crucial that you get good error messages in case you access a non-existing list component.
This version handles this. For error messages purposes this version of the function accepts an
optional parameter, which (somehow redundantly) gives the name of the selector function. |
|
| Program: Example usages of the function make-selector-function. In interaction 1 through 3 we demonstrate generation and use of the first function.
Next we outline how to define accessors of data structures, which are represented as lists.
In reality, we are dealing with list-based record structures. In my every day programming, such list
structures are quite common. It is therefore immensely important, to access data abstractly (via
name accessors, instead of via the position in the list (car, cadr, etc). In this context,
the make-selector-function comes in handy. |
|
| Apply Slide Annotated slide Contents Index References |
|
| Program: Sample usage of apply. |
|
| Mapping and Filtering |
| Program: The forms discussed. |
|
| Classical higher-order functions: Overview Slide Annotated slide Contents Index References | We start with an overview of the classical higher-order functions on lists, not just mapping and filtering, but also including reduction and zipping functions which we cover in subsequent sections. |
|
|
The idea of patterns has been boosted in the recent years, not least in the area of object-oriented programming. The classical higher-order list functions encode recursive patterns on the recursive data type list. As a contrast to many patterns in the object-oriented paradigm, the patterns encoded by map, filter, and others, can be programmed directly. Thus, the algorithmic patterns we study here are not design patterns. Rather, they are programming patterns for the practical functional programmer. |
| Mapping Slide Annotated slide Contents Index References | The idea of mapping is to apply a function on each element of a list, hereby collecting the list of the function applications |
|
| Figure. Mapping a function m on a list. m is applied on every element, and the list of these applications is returned. | 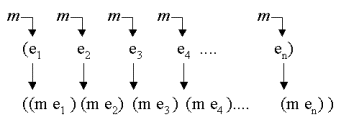 |
|
|
| The mapping function Slide Annotated slide Contents Index References | It is now time to study the implementation of the mapping function. We program a function called mymap in order not to redefine Scheme's own mapping function (a standard function in all Scheme implementations). |
|
| Program: An implementation of map. This is not a good implementation because the recursive call is not a tail call.
We leave it as an exercise to make a memory efficient implementation with tail recursion - see the exercise below. |
|
| Exercise 2.15. Iterative mapping function | In contrast to the function mymap on this page , write an iterative mapping function which is tail recursive. Test your function against mymap on this page, and against the native map function of your Scheme system. |
| Exercise 2.15. Table exercise: transposing, row elimination, and column elimination. | In an earlier section we have shown the application of some very useful table manipulation functions. Now it is time to program these functions, and to study them in further details. Program the functions transpose, eliminate-row, and eliminate-column, as they have been illustrated earlier. As one of the success criteria of this exercise, you should attempt to use higher-order functions as much and well as possible in your solutions. Hint: Program a higher-order function, (eliminate-element n). The function should return a function which eliminates element number n from a list. |
| Examples of mapping Slide Annotated slide Contents Index References | We will now study a number of examples. |
| Table. In the first row we map the string? predicate on a list of atoms (number, symbols, and strings). This reveals (in terms of boolean values) which of the elements that are strings. In the second row of the table, we map a 'multiply with 2' function on a list of numbers. |
|
| Filtering Slide Annotated slide Contents Index References | As the name indicates, the filter function is good for examining elements of a list for a certain property. Only elements which possess the property are allowed through the filter. |
|
| Figure. Filtering a list with a predicate f. The resulting list is the subset of the elements which satisfy f (the elements on which f returns true). |  |
|
|
| The filtering function Slide Annotated slide Contents Index References | The next item on the agenda is an implementation of filter . |
|
| Program: An implementation of filter which is memory efficient. If the predicate holds on an element of the list (the red fragment) we include the element in the result (the brown fragment).
If not (the green fragment), we drop the element from the result (the purple fragment).
|
|
| Exercise 2.16. A straightforward filter function | The filter function illustrated in the material is memory efficient, using tail recursion. Take a moment here to implement the straightforward recursive filtering function, which isn't tail recursive. |
| Examples of filtering Slide Annotated slide Contents Index References | As we did for mapping, we will also here study a number of examples. As before, we arrange the examples in a table where the example expressions are shown to the left, and their values to the right. |
| Table. In the first row we filter the first five natural numbers with the even? predicate. In the second row, we filter the same list of numbers with the odd? predicate. Rather than using the name odd? we form it by calculating (negate even?) . We have seen the higher-order function negate earlier in this lecture. |
|
| Reduction and Zipping |
| Reduction Slide Annotated slide Contents Index References |
|
| Figure. Left and right reduction of a list. Left reduction is - quite naturally - shown to the left, and right reduction to the right. | 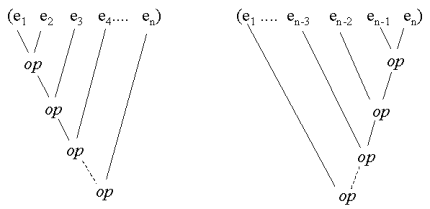 |
|
| The reduction functions Slide Annotated slide Contents Index References |
|
| Program: The function reduce-right. Notice the fit between the composition of the list and the recursive pattern of the
right reduction. |
| Table. Examples of reductions. The - left reduction of the list corresponds to calculating the expression (- (- (- (- 1 2) 3) 4) 5). The - right reduction of the list corresponds to calculating the expression (- 1 (- 2 (- 3 (- 4 5)))). |
|
| Exercise 2.17. Quantifier Functions | The mathematical quantifiers for all and there exists are well-known. In this exercise we will write similar Scheme quantifier functions. The function (for-all lst p) is supposed to check if all elements in the list lst satisfy the predicate p. The function (there-exists lst p) is supposed to check if one or more elements in the list lst satisfy the predicate p. Finally, the function (there-exists-1 lst p) is supposed to check if exactly on element in the list lst satisfies p. Program and test these functions. You should in addition consider how to program these function by use of map, filter, and reduction (accumulation). Please decide if your functions are tail recursive. |
| Accumulation Slide Annotated slide Contents Index References |
|
| Program: The function accumulate-right. The recursive pattern is similar to the pattern of reduce-right. |
| Table. Examples of right accumulations. The first row illustrates that we can accumulate the empty list. The second and third rows are similar to the second and third rows in Table 15.1. |
|
| Zipping Slide Annotated slide Contents Index References |
|
| Figure. Zipping two lists with the function z. The head of the resulting list is (z e i f i), where the element e i comes from the first list, and f i comes from the other. | 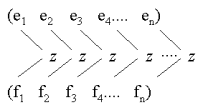 |
| The zipping function Slide Annotated slide Contents Index References |
| Program: The function zip. |
| Table. Examples of zipping. Please notice that (map cons '(1 2 3) '(a b c)) gives the same result as provide that that map accept more than one list. The map in R5RS or R6RS does accept more than one list. If two lists are provided the mapping functions expects two parameters, one from each of the list. |
|
|
| Currying |
| The idea of currying Slide Annotated slide Contents Index References | Currying is the idea of interpreting an arbitrary function to be of one parameter, which returns a possibly intermediate function, which can be used further on in a calculation. |
| The concept currying: Currying allows us to understand every function as taking at most one parameter. Currying can be seen as a way of generating intermediate functions which accept additional parameters to complete a calculation |
| Figure. The signatures of curried functions. In the upper frame we show the signature of a function f, which takes three parameters. The frames below show the signature when f is curried. In the literature, the notation shown to the bottom right is most common. The frame to the left shows how to parse the notation (the symbol -> associates to the right). |  |
|
|
| Currying in Scheme Slide Annotated slide Contents Index References |
|
| Program: Generation of curried and uncurried functions in Scheme. |
|
| Exercise 2.18. Playing with curried functions in Scheme | Try out the functions curry2 and curry3 on a number of different functions. You can, for instance, use then curry functions on plus (+) and map. Demonstrate, by a practical example, that the uncurry functions and the curry functions are inverse to each other. |
| More Exercises Slide Annotated slide Contents Index References |
| Exercise 2.25. Generation of functions with a very flexible signature | Write a function grouping-abstraction-by-predicates (define (grouping-abstraction-by-predicates collector pred1 pred2) ....) with the following characteristics:
Use grouping-abstraction-by-predicates to generate a function that accepts an arbitrary number of parameter. The functions should add all numbers in the parameter list, form a string of all characters in the parameter list, and throw away all others away. Thus, the generated function should return a list of one number and one string. Here is an example:
> (define h (grouping-abstraction-by-predicates
(lambda (l1 l2 l3) (list (sum l1) (apply string l2)))
number?
char?))
> (h 1 3 #\a 4 7 #\b 8 #\c #t 5 #t #t #\d)
(28 "abcd") You may want to play with your function for other purposes, with other predicates, etc. |
| Exercise 2.25. Generalization of curry-2 and curry-3 | On an earlier slide page we have seen how to generate curried functions with 2 and 3 parameters - curry2 and curry3. We have also seen how to generate uncurried functions from curried functions - uncurry2 and uncurry3. Now generalize curry2 and curry3: (define (curry f n) ...) where f is a function with n parameters. Similary, generalize uncurry2 and uncurry3: (define (uncurry cf n) ...) where cf is a curried function with n levels. Test your functions appropriately, and be sure that (uncurry (curry f n) n) is equivalent with f (where f is a function of n parameters). |
| Exercise 2.25. Generalized compose | We have seen the compose function on a previous slide. Let us here work with a variant of compose called self-compose:
(define (self-compose-2 f)
(lambda (x)
(f (f x)))) You first job is to generalize self-compose-2 to self-compose*, which composes the f with itself n times: (define (self-compose* f n) ...) Test your function appropriately. Also, program a function compose* which takes a list of functions as arguments. Each function in the list must be of a single parameter. Your function must return the composition of all the functions. Here is an example of the intended use of the function: > ((compose* (list incr - fac)) 5) -119 fac is here supposed to be the factorial function, and incr is the usual increment function. The expression (compose* (list incr - fac)) should be equivalent to (lambda (x) (incr (- (fac x)))). Are you able to program compose* with a reduction function and compose? |
| Exercise 2.25. Generation of approximations to differentiated functions | Given a function fr from real numbers to real numbers. Program a higher-order function derivative, which differentiates a function like fr. In this exercise you are asked to work numerically, in order to approximate the function. This stands as a contrast to symbolic differentiation. As examples, (derivative (lambda (x) (* x x))) should behave (almost) as (lambda (x) (* 2 x)); (derivate sin) should behave almost as cos; and (derivate exp) should behave almost like exp itself. Write a function compare-2-functions (compare-2-functions f1 f2 numerical-input-list) which applies f1 and f2 on elements in numerical-input-list, and outputs a list of differences between f1(x) and f2(x) for x in numerical-input-list. Use compare-2-functions to compare (derivative f) and f'. The inspiration to the exercise comes from Christian Wagenknecht's book 'Programmierparadigmen', from Springer Verlag. |
| Exercise 2.25. The cartesian product of two sets | Program a function that returns the cartesian product of two sets. Each set should be represented as a list. In this exercise, make as much use of map as possible. You may also use a reduction function, if needed. All the involved iteration over lists should done by mapping or reducing functions. (Do not write your own recursive function that 'just does the job'). |
| Exercise 2.25. Powerset | Program a function powerset, which as input takes a set S (represented as a list). The function must return all possible subsets of S. Hint: What is (powerset '())? It should, of course, be a set of sets. Each set is a represented as a list. |
| Exercise 2.25. Generation of get-prop | In an earlier exercise we programmed an accessor function, get-prop, on property lists. We encountered the following challenges:
Write a function (configure-get-prop comparison-function not-found-value) which returns a get-prop function which uses comparison-function (instead of equal?), which returns not-found-value instead of #f. Generate the get-prop function from the earlier exercise, and generate new variants. Play with your generated functions, and make sure that they work as intended. |
Chapter 2: Recursion and Higher-order Functions
Course home Author home About producing this web Previous lecture (top) Next lecture (top) Previous lecture (bund) Next lecture (bund)
Generated: September 17, 2021, 14:11:24