Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark

Abstract Previous lecture Next lecture Index References Contents

In this lecture we will study how to approach a number of other programming paradigms from the functional programming paradigm - in Scheme. This includes imperative programming and object-oriented programming. Coroutines and trampolining will also be studied.

"NEXT: Point class - basic stuff"

(define (send message obj . par)
  (let ((method (obj message)))
    (apply method par)))

(define (point x y)
  (letrec ((getx    (lambda () x))
           (gety    (lambda () y))
           (add     (lambda (p) 
                      (point 
                       (+ x (send 'getx p))
                       (+ y (send 'gety p)))))
           (type-of (lambda () 'point))
          )
    (lambda (message)
      (cond ((eq? message 'getx) getx)
            ((eq? message 'gety) gety)
            ((eq? message 'add)  add)
            ((eq? message 'type-of) type-of)
            (else (error "Message not understood"))))))

(define p1 (point 1 2))
(define p2 (point 3 4))

(send 'type-of p1)
(list (send 'getx p1) (send 'gety p1))
(define p3 (send 'add p1 p2))
(list (send 'getx p3) (send 'gety p3))


"NEXT: Color point example"

(define (new-instance class . parameters)
  (apply class parameters))

(define (new-part class . parameters)
  (apply class parameters))

(define (method-lookup object selector)
  (cond ((procedure? object) (object selector))
         (else (error "Inappropriate object in method-lookup: " object))))

(define (send message object . args)
  (let ((method (method-lookup object message)))
    (cond ((procedure? method) (apply method args))
          ((null? method) (error "Message not understood: " message))
          (else (error "Inappropriate result of method lookup: " method)))))


(define (object)
  (let ((super '())
        (self 'nil))

   (define (dispatch message)
       '())
 
   (set! self dispatch)
   self))

(define (point x y)
 (let ((super (new-part object))
       (self 'nil))
  (let ((x x) 
        (y y)
       )
     
     (define (getx) x)
  
     (define (gety) y)
  
     (define (add p) 
      (point 
       (+ x (send 'getx p))
       (+ y (send 'gety p))))
  
     (define (type-of) 'point)

     (define (point-info)
       (list (send 'getx self) (send 'gety self) (send 'type-of self)))
       
     (define (dispatch message)
       (cond ((eqv? message 'getx) getx)
             ((eqv? message 'gety) gety)
             ((eqv? message 'add)  add)
             ((eqv? message 'point-info)  point-info)
             ((eqv? message 'type-of) type-of)
  	     (else (method-lookup super message))))
     
     (set! self dispatch)
   )

   self))  


(define (color-point x y color)
 (let ((super (new-part point x y))
       (self 'nil))
   (let ((color color))
       
     (define (get-color)
       color)

     (define (type-of) 'color-point)
       
     (define (dispatch message)
       (cond ((eqv? message 'get-color) get-color)
             ((eqv? message 'type-of) type-of)
             (else (method-lookup super message))))
       
     (set! self dispatch)
   )
     
   self))

(define cp (new-instance color-point 5 6 'red))
(send 'get-color cp)
(list (send 'getx cp) (send 'gety cp))
(send 'type-of cp)
(send 'point-info cp)   ; observe that type-of is not a virtual method

"NEXT: Color point with virtual methods"

(define (new-instance class . parameters)
 (let ((instance (apply class parameters)))
   (virtual-operations instance)
   instance))

; Arrange for virtual operations in object
(define (virtual-operations object)
  (send 'set-self! object object))

(define (new-part class . parameters)
  (apply class parameters))


(define (object)
  (let ((super '())
        (self 'nil))

   (define (set-self! object-part)
     (set! self object-part))

   (define (dispatch message)
     (cond ((eqv? message 'set-self!) set-self!)
           (else '())))
 
   (set! self dispatch)
   self))


(define (point x y)
 (let ((super (new-part object))
       (self 'nil))
  (let ((x x) 
        (y y)
       )
     
     (define (getx) x)
  
     (define (gety) y)
  
     (define (add p) 
      (point 
       (+ x (send 'getx p))
       (+ y (send 'gety p))))
  
     (define (type-of) 'point)

     (define (point-info)
       (list (send 'getx self) (send 'gety self) (send 'type-of self)))

     (define (set-self! object-part)
         (set! self object-part)
         (send 'set-self! super object-part))
       
     (define (dispatch message)
       (cond ((eqv? message 'getx) getx)
             ((eqv? message 'gety) gety)
             ((eqv? message 'add)  add)
             ((eqv? message 'point-info)  point-info)
             ((eqv? message 'type-of) type-of)
             ((eqv? message 'set-self!) set-self!)
             (else (method-lookup super message))))
     
     (set! self dispatch)
   )

   self))  


(define (color-point x y color)
 (let ((super (new-part point x y))
       (self 'nil))
   (let ((color color))
       
     (define (get-color)
       color)

     (define (type-of) 'color-point)

     (define (set-self! object-part)
         (set! self object-part)
         (send 'set-self! super object-part))
       
     (define (dispatch message)
       (cond ((eqv? message 'get-color) get-color)
             ((eqv? message 'type-of) type-of)
             ((eqv? message 'set-self!) set-self!)
             (else (method-lookup super message))))
       
     (set! self dispatch)
   )
     
   self))

(define cp (new-instance color-point 5 6 'red))
(send 'get-color cp)
(list (send 'getx cp) (send 'gety cp))
(send 'type-of cp)
(send 'point-info cp)

"NEXT: Trampolining 1"

(define (fact-iter n acc)
  (if (zero? n)
      acc
      (fact-iter
        (- n 1)
        (* acc n))))

(fact-iter 5 1)

(define (mem? n lst)
  (cond ((null? lst) #f)
        ((= (car lst ) n) #t)
        (else (mem? n (cdr lst)))))

(mem? 5 (list 1 2 3 4 5 6))

(define (fib n)
  (fib-iter n 0 0 1))

(define (fib-iter n i small large)
  (if (< i n)
      (fib-iter n (+ i 1) large (+ large small))
      small))

(fib 8)

"NEXT: Trampolining 2"
(define (return x) x)             
(define (bounce thunk) (call thunk))     
(define (call thunk) (thunk))    

(define (fact-iter n acc)
  (if (zero? n)
      (return acc)
      (bounce 
        (lambda ()
          (fact-iter
            (- n 1)
            (* acc n))))))

(fact-iter 5 1)

(define (mem? n lst)
  (cond ((null? lst) (return #f))
        ((= (car lst ) n) (return #t))
        (else (bounce
                (lambda ()
                  (mem? n (cdr lst)))))))

(mem? 5 (list 1 2 3 4 5 6))

(define (fib n)
  (fib-iter n 0 0 1))

(define (fib-iter n i small large)
  (if (< i n)
      (bounce
        (lambda () 
          (fib-iter n (+ i 1) large (+ large small))))
      (return small)))

(fib 8)

"NEXT: Trampolining 3"

(define (return x) (tag 'done x))                 
(define (bounce thunk) (tag 'doing thunk))        
(define (tag label thing) (cons label thing))     

(define (fact-iter n acc)
  (if (zero? n)
      (return acc)
      (bounce 
        (lambda ()
          (fact-iter
            (- n 1)
            (* acc n))))))

(fact-iter 5 1)

(define (mem? n lst)
  (cond ((null? lst) (return #f))
        ((= (car lst ) n) (return #t))
        (else (bounce
                (lambda ()
                  (mem? n (cdr lst)))))))

(mem? 5 (list 1 2 3 4 5 6))

(define (fib n)
  (fib-iter n 0 0 1))

(define (fib-iter n i small large)
  (if (< i n)
      (bounce
        (lambda () 
          (fib-iter n (+ i 1) large (+ large small))))
      (return small)))

(fib 8)

"NEXT: Trampolining 4"

(define (tag label thing) (cons label thing))
(define tag-of car)
(define tag-value cdr)

(define (pogo-stick thread)                                
  (cond ((eqv? 'done (tag-of thread))                      
          (tag-value thread))                              
        ((eqv? 'doing (tag-of thread))                     
          (pogo-stick (call (tag-value thread))))))          

(define (fact-iter n acc)
  (if (zero? n)
      (return acc)
      (bounce 
        (lambda ()
          (fact-iter
            (- n 1)
            (* acc n))))))

(pogo-stick (fact-iter 5 1))

(define (mem? n lst)
  (cond ((null? lst) (return #f))
        ((= (car lst ) n) (return #t))
        (else (bounce
                (lambda ()
                  (mem? n (cdr lst)))))))

(pogo-stick (mem? 5 (list 1 2 3 4 5 6)))

(define (fib n)
  (fib-iter n 0 0 1))

(define (fib-iter n i small large)
  (if (< i n)
      (bounce
        (lambda () 
          (fib-iter n (+ i 1) large (+ large small))))
      (return small)))

(pogo-stick (fib 8))

"NEXT: Trampolining 5"

(define (seesaw thread-1 thread-2)                           
  (cond ((eqv? 'done (tag-of thread-1))                      
          (tag-value thread-1))
        ((eqv? 'doing (tag-of thread-1))
          (seesaw thread-2 (call (tag-value thread-1))))))

(define (fact-iter n acc)
  (if (zero? n)
      (return acc)
      (bounce 
        (lambda ()
          (fact-iter
            (- n 1)
            (* acc n))))))

(define (fib n)
  (fib-iter n 0 0 1))

(define (fib-iter n i small large)
  (if (< i n)
      (bounce
        (lambda () 
          (fib-iter n (+ i 1) large (+ large small))))
      (return small)))


(seesaw (fact-iter 5 1) (fib 8))
(seesaw (fact-iter -1 1) (fib 8))



"NEXT: Trampolining 6"

(define (trampoline thread-queue)                            
  (let ((head (car thread-queue)))
   (cond ((eqv? 'done (tag-of head)) (tag-value head))
         ((eqv? 'doing (tag-of head)) 
             (trampoline
                (append 
                   (cdr thread-queue)
                   (list (call (tag-value head)))))))))

(define (fact-iter n acc)
  (if (zero? n)
      (return acc)
      (bounce 
        (lambda ()
          (fact-iter
            (- n 1)
            (* acc n))))))

(define (mem? n lst)
  (cond ((null? lst) (return #f))
        ((= (car lst ) n) (return #t))
        (else (bounce
                (lambda ()
                  (mem? n (cdr lst)))))))

(define (fib n)
  (fib-iter n 0 0 1))

(define (fib-iter n i small large)
  (if (< i n)
      (bounce
        (lambda () 
          (fib-iter n (+ i 1) large (+ large small))))
      (return small)))

(trampoline (list (fact-iter -1 1) (mem? 5 (list 2 8 9 1 3 4  3 5 )) (fib 8)))

(trampoline (list (fact-iter -1 1) (fib 7)  (mem? 5 (list 2 8 9 1 3 4  3 5 ))))

"THE END"

Functions and closures revisited Slide Annotated slide Contents Index References

On this page we review some of the properties of function object - also known as closures. The contents of this pages is taken directly from an earlier pages in this material.

The concept function object: A function object represents a function at run time. A function object is created as the value of a lambda expression		A function object is a first class value at run time, in the same way as numbers, lists and other data are values. This is different from more traditional programming languages, where procedural and functional abstractions have another status than ordinary data.
The concept closure: A function object is also known as a closure.		The name 'closure' is related to the interpretation of free names in the body expression of the function. Free names are used, but not defined in the body. In a function object (or closure) the free names are bound in the context of the lambda expression. This is a contrast to the case where the free names are bound in the context of the application of the function.

Characteristics of function objects: First class A function object can be passed as a parameter to a function, returned as the result from another function, and organized as a constituent of a data structure Anonymous Does not have a name Closure Free names are captured in the context of the lambda expression Static binding of free names A closure is represented as a pair of the syntactical form of the function and values of free names Callable A function object can be applied on actual parameters

Reference Foldoc: closure

Classes and objects Slide Annotated slide Contents Index References

Due to (1) the first class status of functions, and due to (2) the use of static binding of free names, it is possible to interpret a closure as an object With this interpretation, it is possible to regard certain function definitions as classes

Object model: Objects are instances of classes Objects interact by means of message passing Methods are dynamically looked up (in the classes behind the objects) All methods are virtual

Program: The definition of a 'class Point ' with methods getx , gety , add , and type-of. On this page we have also defined the syntactical convenience function send that sends a message to an object. In Racket be sure that you define send before Point (such that send in the add method refers to our send , and not an already existing and unrelated definition of the name send ).

(define (point x y) (letrec ((getx (lambda () x)) (gety (lambda () y)) (add (lambda (p) (point (+ x (send 'getx p)) (+ y (send 'gety p))))) (type-of (lambda () 'point)) ) (lambda (message) (cond ((eq? message 'getx) getx) ((eq? message 'gety) gety) ((eq? message 'add) add) ((eq? message 'type-of) type-of) (else (error "Message not understood"))))))

Program: The send method which is used in the Point class. The function apply calls a function on a list of parameters. This should be seen in contrast to a normal call, in which the individual parameters are passed.

(define (send message obj . par) (let ((method (obj message))) (apply method par)))

Exercise 3.2. Points and Rectangle

The purpose of this exercise is to strengthen your understanding of functions used as classes in Scheme. First, play with the existing Point class defined on this page available from the on-line version of this material. As an example, construct two points and add them together. Also, construct two lists of each four points, and add them together pair by pair. Define a new method in the Point class called (move dx dy), which displaces a point with dx units in the x direction and dy units in the y direction. We encourage you to make a functional solution in which move creates a new displaced point. (After that you may consider an imperative solution, in which the state of the receiving point can be changed with an assignment, set!). Finally, define a new class, Rectangle, which aggregates two points to a representation of a rectangle. Define move and area methods in the new class. As a practical remark to the 'class Point ' and the send primitive, be sure to define send before you define Point . (This is done to redefine an existing send procedure in Racket).

A general pattern of classes Slide Annotated slide Contents Index References

The following shows a template of a function that serves as a class

Program: A general template of a simulated class. construction-parameters are typically transferred to the let construct, which we want to play the role as instance variables. Next comes explicitly defined methods, and last is the object handle called self . Notice that the value returned by the class is the value of self - the object handle.

(define (class-name construction-parameters) (let ((instance-var init-value) ...) (define (method parameter-list) method-body) ... (define (self message) (cond ((eqv? message selector) method) ... (else (error "Message not understood" message)))) self))

Program: Accompanying functions for instantiation and message passing.

(define (new-instance class . parameters) (apply class parameters)) (define (send message object . args) (let ((method (method-lookup object message))) (cond ((procedure? method) (apply method args)) (else (error "Error in method lookup " method))))) (define (method-lookup object selector) (cond ((procedure? object) (object selector)) (else (error "Inappropriate object in method-lookup: " object))))

Reference Kurt Nørmark, Simulation of Object-oriented Concepts and Mechanisms in Scheme

Example of the general class pattern Slide Annotated slide Contents Index References

The Point class redefined to comply with the general class pattern

Program: The class Point implemented with use of the general class template. The Point class corresponds to the Point class defined on an earlier page. Notice that the bindings of x and y in the let construct is superfluous in the example. But due to the simultaneous name binding used in let constructs, they make sense. Admittedly, however, the let construct looks a little strange.

(define (point x y) (let ((x x) (y y) ) (define (getx) x) (define (gety) y) (define (add p) (point (+ x (send 'getx p)) (+ y (send 'gety p)))) (define (type-of) 'point) (define (self message) (cond ((eqv? message 'getx) getx) ((eqv? message 'gety) gety) ((eqv? message 'add) add) ((eqv? message 'type-of) type-of) (else (error "Message not understood" message)))) self))

Program: All the necessary stuff to play with Point.

Program: A sample construction and dialogue with point.

1> (define p (new-instance point 2 3)) 2> (send 'getx p) 2 3> (define q (new-instance point 4 5)) 4> (define p+q (send 'add p q)) 5> (send 'getx p+q) 6 6> (send 'gety p+q) 8

A general pattern of classes with inheritance Slide Annotated slide Contents Index References

The following shows a template of a function that serves as a subclass of another class

Program: A general template of a simulated class with inheritance.

(define (class-name parameters) (let ((super (new-part super-class-name some-parameters)) (self 'nil)) (let ((instance-variable init-value) ...) (define (method parameter-list) method-body) ... (define (dispatch message) (cond ((eqv? message 'selector) method) ... (else (method-lookup super message)))) (set! self dispatch)) self))

Program: The root of a class hierarchy.

(define (object) (let ((super '()) (self 'nil)) (define (dispatch message) '()) (set! self dispatch) self))

Program: Accompanying functions for instantiation, message passing, and method lookup.

(define (new-instance class . parameters) (apply class parameters)) (define (new-part class . parameters) (apply class parameters)) (define (method-lookup object selector) (cond ((procedure? object) (object selector)) (else (error "Inappropriate object in method-lookup: " object)))) (define (send message object . args) (let ((method (method-lookup object message))) (cond ((procedure? method) (apply method args)) ((null? method) (error "Message not understood: " message)) (else (error "Inappropriate result of method lookup: " method)))))

An example of classes with inheritance Slide Annotated slide Contents Index References

We sketch one of the favorite toy specializations of Point - ColorPoint

Program: A specialization of Point which is called ColorPoint.

(define (color-point x y color) (let ((super (new-part point x y)) (self 'nil)) (let ((color color)) (define (get-color) color) (define (type-of) 'color-point) (define (dispatch message) (cond ((eqv? message 'get-color) get-color) ((eqv? message 'type-of) type-of) (else (method-lookup super message)))) (set! self dispatch) ) self))

Program: Class Point - A subclass of object - with a new method point-info.

(define (point x y) (let ((super (new-part object)) (self 'nil)) (let ((x x) (y y) ) (define (getx) x) (define (gety) y) (define (add p) (point (+ x (send 'getx p)) (+ y (send 'gety p)))) (define (type-of) 'point) (define (point-info) (list (send 'getx self) (send 'gety self) (send 'type-of self))) (define (dispatch message) (cond ((eqv? message 'getx) getx) ((eqv? message 'gety) gety) ((eqv? message 'add) add) ((eqv? message 'point-info) point-info) ((eqv? message 'type-of) type-of) (else (method-lookup super message)))) (set! self dispatch) ) self))

Program: All necessary stuff to play with ColorPoint.

Program: A sample construction and sample dialogue with ColorPoint.

> (define cp (new-instance color-point 5 6 'red)) > (send 'get-color cp) red > (send 'getx cp) 5 > (send 'gety cp) 6 > (send 'point-info cp) (5 6 point) > (define cp-1 (send 'add cp (new-instance color-point 1 2 'green))) > (send 'getx cp-1) 6 > (send 'gety cp-1) 8 > (send 'get-color cp-1) Message not understood: get-color > (send 'type-of cp-1) point > (send 'point-info cp-1) (6 8 point)

The interpretation of self Slide Annotated slide Contents Index References

In order to obtain virtual methods of classes we need to alter the value of self in all superclasses

Figure. Two different interpretations of self . We see two linear class hierarchies. The class C inherits from B, which in turn inherits from A. And similarly, F inherits from E, which inherits from D. The one to the left - in the green class hierarchy - is the naive one we have obtained in our templates and examples until now. The one to the right - in the yellow class hierarchy, shows another interpretation of self . Following this interpretation, self at all levels refer to the most specialized object part.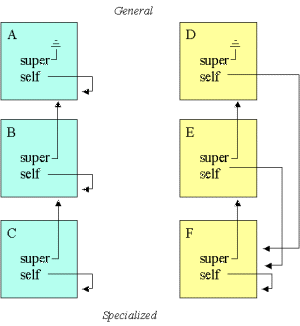

A general pattern of a class hierarchy with virtual methods Slide Annotated slide Contents Index References

The following shows a template of a function that serves as a subclass of another class - now with virtual methods

Program: A general template of a simulated class with inheritance.

(define (class-name parameters) (let ((super (new-part super-class-name some-parameters)) (self 'nil)) (let ((instance-variable init-value) ...) (define (method parameter-list) method-body) ... (define (set-self! object-part) (set! self object-part) (send 'set-self! super object-part)) (define (dispatch message) (cond ((eqv? message 'selector) method) ... ((eqv? message 'set-self) set-self!) (else (method-lookup super message)))) (set! self dispatch)) self))

Program: The functions new-instance, virtual-operations, and others.

An example of virtual methods Slide Annotated slide Contents Index References

We continue playing with the classes Point and ColorPoint

Program: All necessary stuff to play with ColorPoint.

Program: A sample construction and sample dialogue with ColorPoint.

> (define cp (new-instance color-point 5 6 'red)) > (send 'get-color cp) red > (send 'getx cp) 5 > (send 'gety cp) 6 > (send 'point-info cp) (5 6 color-point) > (define cp-1 (send 'add cp (new-instance color-point 1 2 'green))) > (send 'point-info cp-1) (6 8 point) > (send 'get-color cp-1) Message not understood: get-color

Exercise 3.4. Color Point Extensions

On this page we have seen the class ColorPoint, which inherits from Point. The classes make use of virtual methods. In this exercise you should start with the code in this file. First take a look at the existing stuff, and make sure you understand it. Be aware that both of the classes Point and ColorPoint use virtual methods. Add a method class-of to both Point and ColorPoint that returns the class of an instance. Now repair the method add in Point, such that it always instantiate a class corresponding to the class of the receiver. In other words, if the receiver of add is a Point, instantiate a Point. If the receiver of add is a ColorPoint, instantiate a ColorPoint. You can probably use the method class-of from above. You may encounter a problem, because the constructor of point and color-point take a different number of parameters. You are welcome to default the color of a color point to your favorite color!

Exercise 3.4. Representing HTML with objects in Scheme

This is an open exercise - maybe the start of a minor project - The exercises relates to LAML. I do not recommend this exercise in this variant of PP. In the original mirror of HTML in Scheme, the HTML mirror functions, return strings. In the current version, the mirror functions return an internal syntax tree representation of the web documents. With this, it is realistic to validate a document against a grammar while it is constructed. In this exercise we will experiment with an object representation of a web document. We will use the class and object representation which we have introduced in this lecture. Construct a general class html-element which implement the general properties of a HTML element object. These include: A method that generates a rendering of the element A method that returns the list of constituents An abstract method that performs context free validation of the element In addition, construct one or more examples of specific subclasses of html-element , such as html , head , or body. These subclasses should have methods to access particular, required constituents of an element instance, such as the head and the body of a HTML element, and title of a head element. Also, the concrete validation predicate must be redefined for each specific element.

Summing up: Simulation of OOP in Scheme Slide Annotated slide Contents Index References

What have we learned?

Closures can serve as objects Functions can serve as classes The tricks is the dispatcher A sequence of object parts may be used to represent inheritance The trick is to arrange for virtual methods Even more can be achieved See my report on Simulation of OOP in Scheme

Do not necessarily use OOP simulation for handling of concept in your real-life Scheme programs.

To which degree can we do imperative programming in a functional programming language?

Points of interest Sequential control Jumps and goto Selection control Iteration control Assignment State transitioning

Sequential Control Slide Annotated slide Contents Index References

Evaluation order is very liberal in functional programming languages Can we deal with sequential order, as known from imperative programming languages?

Begin C1; C2 End Classical, Algol-like syntax for sequential execution. C1 first, next C2. {C1; C2;} A block in C that ensures sequential composition of two commands C1 and C2. E1, E2 An expression with the comma operator that ensures sequential evaluation of of two expressions E1 and E2. ((lambda (a b) unused) C1 C2) Using parameters to a non-curried lambda expression - does not work The evaluation order of C1 and C2 is not known ((lambda (unused) C2) C1) The actual parameter C1 is evaluated - and bound to unused - before the evaluation of C2. The rule in languages with applicative order evaluation - such as Scheme (begin C1 C2) A Scheme special form (library syntax) for sequential composition The value of (begin C1 C2) is the value of C2 Similar to the comma operator in C Rarely useful in functional programming

Jumps in Functional Programs Slide Annotated slide Contents Index References

A tail call in Scheme is like a goto with parameters [Insight originally observed by Guy Steele]

Table. Programs with goto. In the Scheme expression, notice that the calls of L2 (twice) and L1 (once) in L1 are all tail calls. Therefore in these calls, there is no need to return to L1 after the simulation of a goto. Consequently, we simple leave L1 when/if L1 or L2 is called.

Imperative Functional - Scheme Begin L1: if B1 then goto L2; S1; if B2 then goto L2; S2; goto L1; L2: S3; End - /* Rewritten - equivalent */ Begin L1: if B1 then goto L2; else begin S1; if B2 then goto L2; else begin S2; goto L1; end end L2: S3; End (letrec ((L1 (lambda () (if B1 (L2) (begin S1 (if B2 (L2) (begin S2 (L1))))))) (L2 (lambda () S3))) (L1)) #include #define DUMMY 0 int main(void) { int B1 = 1, B2 = 1; int S1 = DUMMY, S2 = DUMMY, S3 = DUMMY; L1: if (B1) goto L2; S1; if (B2) goto L2; S2; goto L1; L2: S3; } Same

Reference Example from 'Lambda the Ultimate' by Steele and Sussman

A labelled program part becomes a function A goto statement becomes a tail call to one of the functions

Selection Control Slide Annotated slide Contents Index References

Conditionals are fundamental and both the functional and the imperative programming paradigm

(if C E1 E2) Considered a core primitive in applicative functional programming languages Only one of the expressions E1 and E2 should be evaluated Similar to the if control structure in imperative programming languages

Reference Core Scheme

Iterative Control Slide Annotated slide Contents Index References

Iterative control is handled by recursion in functional programming languages

Iterative functions Programmed with recursion in tail calls - tail recursion Memory efficient Every loop requires a named, recursive function

Table. Euclid's gcd function programming in C with a while loop, and in Scheme with a tail recursive function

Imperative Functional - Scheme int gcd(int small, int large){ int rem; while (small > 0){ rem = large % small; large = small; small = rem; } return large; } (define (gcd small large) (if (> small 0) (gcd (remainder large small) small) large))

Assignments in Functional Programs Slide Annotated slide Contents Index References

General use of assignment is hard to simulate in a functional program Assignment for name binding purposes - single assignment - can be handled by name bindings in lambda expressions

Table. We illustrate the handling of single assignments (first row)

Imperative Functional - Scheme void solveQuadraticEquation (double a, double b, double c){ double discriminant, root1, root2; discriminant = b * b - 4 * a * c; if (discriminant < 0) printf("No roots\n"); else if (discriminant == 0){ root1 = -b/(2*a); printf("One root: %f\n", root1); } else { root1 = (-b + sqrt(discriminant))/(2*a); root2 = (-b - sqrt(discriminant))/(2*a); printf("Two roots: %f and %f\n", root1, root2); } } (define (solveQuadraticEquation a b c) (let ((discriminant (- (* b b) (* 4 a c)))) (cond ((< discriminant 0) (list)) ((= discriminant 0) (let ((root1 (/ (- b) (* 2 a)))) (list root1))) (else (let ((root1 (/ (+ (- b) (sqrt discriminant)) (* 2 a))) (root2 (/ (- (- b) (sqrt discriminant)) (* 2 a)))) (list root1 root2)))))) void solveQuadraticEquation (double a, double b, double c){ double discriminant = b * b - 4 * a * c; if (discriminant < 0) printf("No roots\n"); else if (discriminant == 0){ double root1 = -b/(2*a); printf("One root: %f\n", root1); } else { double root1 = (-b + sqrt(discriminant))/(2*a); double root2 = (-b - sqrt(discriminant))/(2*a); printf("Two roots: %f and %f\n", root1, root2); } } Same

State in Functional Programs Slide Annotated slide Contents Index References

State transitioning - where a set of variables are updated simultaneously - can be dealt with by parameter passing - typically in a tail recursive function

Table. We illustrate the handling of state transitioning

Imperative Functional - Scheme int gcd(int small, int large){ int rem; while (small > 0){ rem = large % small; large = small; small = rem; } return large; } (define (gcd small large) (if (> small 0) (gcd (remainder large small) small) large))

Object Mutation Slide Annotated slide Contents Index References

Object mutation in imperative programming (or object-oriented programming) can be dealt with by functions that return a mutated copy of the object.

Table. We illustrate object mutation - a point in C and Scheme. In Scheme we use a cons pair for the x and y coordinates.

Imperative Functional - Scheme #include struct point{ double x, y; }; typedef struct point point; void move(point *p, double dx, double dy){ p->x += dx; p->y += dy; } int main(void) { point p = {5.0, 7.0}; printf("p: (%lf, %lf)\n", p.x, p.y); move(&p, 1.0, 2.0); printf("p: (%lf, %lf)\n", p.x, p.y); return 0; } (define (make-point x y) (list 'point x y)) (define point-x (compose car cdr)) (define point-y (compose car (compose cdr cdr))) (define p (make-point 5.0 7.0)) (define (move p dx dy) (make-point (+ (point-x p) dx) (+ (point-y p) dy))) > p (point 5.0 7.0) > (define q (move p 1 2)) > q (point 6.0 9.0)

It is sometimes necessary to escape from a deep expression, for instance in an exceptional case We are interested in a primitive which allows us to control the remaining part of a calculation - a so-called continuation.

Exit or exception mechanism: The need to abandon some deep evaluation Continuation Capturing of continuations Exploring new control mechanisms by use of continuations

Scheme supports first class continuations dressed as functions

The catch and throw idea Slide Annotated slide Contents Index References

Catch and throw provides for an intuitively simple escape mechanism on functional ground

Syntax:

(catch id catch-expr)

Syntax:

(throw id throw-expression)

Scheme does not support catch and throw Instead, Scheme supports a much more powerful mechanisms based on continuations

References Common Lisp the Language, 2nd Edition. Dynamic Non-local exists (Common Lisp)

A catch and throw example Slide Annotated slide Contents Index References

We now give a Common Lisp like example of catch and throw.

Exit from a list length function in case it discovers a non-empty tail of the list

Program: An example using catch and throw. Please notice that the example is not a proper Scheme program. Catch and throw are not defined in Scheme.

(define (list-length lst) (catch 'exit (letrec ((list-length1 (lambda (lst) (cond ((null? lst) 0) ((pair? lst) (+ 1 (list-length1 (cdr lst)))) (else (throw 'exit 'improper-list)))))) (list-length1 lst))))

Reference Same example with call-with-current-continuation

catch and throw are not available in standard Scheme

The intuition behind continuations Slide Annotated slide Contents Index References

The concept continuation: A continuation of the evaluation of an expression E in a surrounding context C represents the future of the computation, which waits for, and depends on, the value of E

Table. An intuitive understanding of continuations of an expression in some context.

Context C and expression E Intuitive continuation of E in C (+ 5 (* 4 3)) The adding of 5 to the value of E (cons 1 (cons 2 (cons 3 '()))) The consing of 3, 2 and 1 to the value of E (define x 5) (if (= 0 x) 'undefined (remainder (* (+ x 1) (- x 1)) x)) The multiplication of E by x - 1 followed by a the calculation of the remainder by division of x

Being more precise Slide Annotated slide Contents Index References

Instead of relying of an informal understanding of continuations we will now introduce lambda expressions that represent the continuations.

We can form a lambda expression that to some degree represents a continuation

Table. A more precise notation of the continuations of E

Context C and expression E The continuation of E in C (+ 5 (* 4 3)) (lambda (E) (+ 5 E)) (cons 1 (cons 2 (cons 3 '()))) (lambda (E) (cons 1 (cons 2 (cons 3 E)))) (define x 5) (if (= 0 x) 'undefined (remainder (* (+ x 1) (- x 1)) x)) (lambda (E) (remainder (* E (- x 1)) x))

The capturing of continuations Slide Annotated slide Contents Index References

It is now time to introduce the Scheme primitive that allows us to capture a continuation.

Scheme provides a primitive that captures a continuation of an expression E in a context C. The primitive is called call-with-current-continuation, or call/cc as a short alias. call/cc takes a parameter, which is a function of one parameter. The parameter of the function is bound to the continuation.

Table. Use of call/cc and capturing of continuations.

Context C and the capturing (+ 5 (call/cc (lambda (e) (* 4 3)) )) (cons 1 (cons 2 (cons 3 (call/cc (lambda (e) '()) )))) (define x 5) (if (= 0 x) 'undefined (remainder (* (call/cc (lambda (e) (+ x 1)) ) (- x 1)) x))

Capturing, storing, and applying continuations Slide Annotated slide Contents Index References

We here show capturing, imperative assignment, and a subsequent application of a continuation

Table. Capturing and applying continuations. The captured continuations are stored in a global variable. The application of the continuation is shown in the third column, and the result of the application of the continuation is shown in the fourth column.

Context C and expression E Value of C Application of continuation Value (+ 5 (call/cc (lambda (e) (set! cont-remember e) (* 4 3)))) 17 (cont-remember 3) 8 (cons 1 (cons 2 (cons 3 (call/cc (lambda (e) (set! cont-remember e) '()))))) (1 2 3) (cont-remember '(7 8)) (1 2 3 7 8) (define x 5) (if (= 0 x) 'undefined (remainder (* (call/cc (lambda (e) (set! cont-remember e) (+ x 1) )) (- x 1)) x)) 4 (cont-remember 3) 2

Use of continuations for escaping purposes Slide Annotated slide Contents Index References

We here illustrate applications of the continuations for escaping purposes

Table. Capturing and use of a continuation for escaping purposes

Context C, capturing, and escape call Value (+ 5 (call/cc (lambda (e) (* 4 (e 10)))) ) 15 (cons 1 (call/cc (lambda (e) (cons 2 (cons 3 (e 'x))))) ) (1 . x) (define x 5) (if (= 0 x) 'undefined (call/cc (lambda (e) (remainder (* (+ x 1) (- x (e 111))) x))) ) 111

Practical example: Length of an improper list Slide Annotated slide Contents Index References

The length of an improper list is undefined We chose to return the symbol improper-list if list-length encounters an improper list This example is similar to the catch and throw example shown earlier in this section

Program: The function list-length, which returns the symbol 'improper-list in case it encounters an improper list.

(define (list-length l) (call-with-current-continuation (lambda (do-exit) (letrec ((list-length1 (lambda (l) (cond ((null? l) 0) ((pair? l) (+ 1 (list-length1 (cdr l)))) (else (do-exit 'improper-list)))))) (list-length1 l))) ))

Reference An continuation passing style version of list-length - without use of call-with-current-continuation

Practical example: Searching a binary tree Slide Annotated slide Contents Index References

Searching a binary tree involves a recursively defined tree traversal. If we find the node we are looking for it is convenient to throw the node out of the tree traversal. Notice the slightly 'imperative style' in find-in-tree below.

Program: A tree search function which uses a continuation found if we find what we search for. Notice that this examples requires the function subtree-list, in order to work. The function returns #f in case we do not find node we are looking for. Notice that it makes sense in this example to have both the if expression and the #f value in sequence!

(define (find-in-tree tree pred) (call-with-current-continuation (lambda (found) (letrec ((find-in-tree1 (lambda (tree pred) (if (pred tree) (found tree) (let ((subtrees (subtree-list tree))) (for-each (lambda (subtree) (find-in-tree1 subtree pred)) subtrees))) #f))) (find-in-tree1 tree pred))) ))

Reference Coroutines

We will see more examples of continuation programming in the lecture about 'Simulation of Other Paradigms in Scheme': Coroutines

The implicite continuation of a function is turned into an explicit parameter Every function takes an extra parameter: A continuation which is a function of a single parameter No function returns normally

Reference Continuations

Program: A function programmed in both direct style and continuation passing style.

(define (p-direct a b) (* (+ a b) (- a b))) (define (p-cps a b k0) (plus a b (lambda(v1) ; given the sum of and b in v1, now compute a-b and ; the product. (sub a b (lambda(v2) ; given the sum in v1 and the difference in v2, now ; carry out the rest of the computation (the multiplication) ; and pass the result to k0. (mult v1 v2 k0)))))) ; Variants of +, -, and * with continuation parameters. (define (plus a b k) (k (+ a b ))) (define (sub a b k) (k (- a b))) (define (mult a b k) (k (* a b)))

Program: Functions w, f, g and h programmed in direct style.

(define (w a b) (f (g a) (h b) (g b) (h a))) (define (f a b c d) (+ a b c d)) (define (g a) (* a a)) (define (h a) (* a a a))

Program: The same functions programmed in continuation passing style.

; (define (w a b) (f (g a) (h b) (g b) (h a))) ; (define (f a b c d) (+ a b c d)) ; (define (g a) (* a a)) ; (define (h a) (* a a a)) (define (w a b k0) (g a (lambda(v1) (h b (lambda (v2) (g b (lambda (v3) (h a (lambda (v4) (f v1 v2 v3 v4 k0)))))))))) (define (f a b c d k) (k (+ a b c d))) (define (g a k) (k (* a a))) (define (h a k) (k (* a a a)))

Exercise 3.5. A discriminant function in continuation passing style

Program the following discriminant function (lambda (a b c) (- (* b b) (* 4 a c))) in continuation passing style (CPS). (define (discriminant a b c) (sub (square b) (mult (mult 4 a) c))) ; AUX functions: (define (square a) (mult a a)) (define (mult a b) (* a b)) (define (sub a b) (- a b)) In the program above we have provided auxilliary functions for squaring, multiplication and subtraction. These functions must be provided with an extra continuation parameter when you program the CPS variants of the functions. Consider different evaluation orders, and how it affects the CPS variant of the functions.

Reference Recursion versus iteration

Program: The usual recursive factorial function - in direct and continuation passing style.

(define (fact-direct n) (if (= n 0) 1 (* n (fact-direct (- n 1))))) (define (fact-cps n k) (if (= n 0) (k 1) (fact-cps (- n 1) (lambda(v) ; Eventually v becomes (- n 1)! (k (* n v))) ; Now pass (* n v) = (* n (- n 1)! ) to k. ) ) ) ; Notice that fact-cps is tail recursive!

Program: The tail recursive factorial function - in direct and continuation passing style.

(define (fact-tail-rec n r) (if (= 0 n) r (fact-tail-rec (- n 1) (* r n)))) (define (fact-tail-rec-cps-1 n r k) (if (= 0 n) (k r) (fact-tail-rec-cps-1 (- n 1) (* r n) (lambda (v) ; Eventually v becomes (fact n), because the base case passes (k v)) ; the result via a chain of trivial "pass on" functions. ; Are all these (lambda(v) (k v)) functions really necessary? ) ; No - see the next variant called fact-tail-rec-cps-2. ) ) (define (fact-tail-rec-cps-2 n r k) (if (= 0 n) (k r) (fact-tail-rec-cps-2 (- n 1) (* r n) k ; Eventually (fact n) is passed to k. k is the continuation ) ; of the original call to the factorial function. ) )

Program: The list-length function - continuation passing style - handling improper lists.

; list-length in direct style - makes use of call-with-current-continuation to capture the outer continuation. (define (list-length-direct lst) (call-with-current-continuation (lambda (do-exit) (letrec ((list-length-inner (lambda (lst) (cond ((null? lst) 0) ((pair? lst) (+ 1 (list-length-inner (cdr lst)))) (else (do-exit 'improper-list)))))) (list-length-inner lst))) )) (define (list-length-cps lst k0) ; k0 is the outer continuation - ready to catch exceptional values (letrec ((list-length-inner (lambda (lst k1) (cond ((null? lst) (k1 0)) ((pair? lst) (list-length-inner (cdr lst) (lambda (v) (k1 (+ 1 v))) ; v is the length of (cdr l). ; Pass 1+v to k1. ) ) (else (k0 'improper-list)))) )) ; Pass the symbol improper-list ; to the outer continuation k0. (list-length-inner lst k0))) ; The outer continuation k0 is used for 'returning' exceptional values. ; A chain of inner continations on the form (lambda (v) (k1 (+ 1 v))) accumulate the length. ; Heavy and clumsy. Next we show a much more elegant iterative version.

Program: An iterative list-length function - continuation passing style - handling improper lists.

(define (list-length-iter-cps lst res k0) (cond ((null? lst) (k0 res)) ((pair? lst) (list-length-iter-cps (cdr lst) (+ res 1) k0)) (else (k0 'improper-list)))) ; k0 is passed along the tail recursive calls, and ; can also be used for passing 'an exceptional value'.

Reference An earlier version of list-length that use call-with-current-continuation

Observations about continuation passing style Slide Annotated slide Contents Index References

Based on the experiences with the programs on the previous page we make some observations about continuation passing style - CPS

Functions written in CPS are always tail recursive In some cases at the expense of construction of a chain of lambda expressions - to be called when the recursion contracts Tail recursive functions do not need to contruct new continuations The original - outer continuation - is passed on in recursive calls Functions written in CPS do not need 'the magic primitive' call-with-current-continuation We can program in such a way that the necessary continuations are explicitly available Functions written in CPS are specific about the evaluation order of sub-expressions Functions written in CPS are 'convoluted', 'inverted' and difficult to read and write Functions in CPS are typically automatically translated from functions in direct style Functions written in CPS never returns Can be implemented without a run time stack

A function F1 that calls a function F2 are not symmetric - If F2 is called several times it restarts every time Two coroutines C1 and C2 cooperate in a fully symmetric way - by resuming each other.

Figure. The flow of control among functions (F1 calls F2) left, and among coroutines (C1 and C2 resume each other).

Simulating Coroutines in Scheme Slide Annotated slide Contents Index References

Coroutines can be simulated in Scheme by (heavy) use of continuations

Upon resuming C2 from C1 Activate a continuation cont2 in C2 - pass some value v Also send the current continuation cont1 of the resume point in C1 C2 receives an aggregate consisting of: (v , cont1)

Program: Template for resuming C2 from C1.

A simpel producer and consumer Slide Annotated slide Contents Index References

We show two different variants of a simple producer consumer pattern

Program: Producer Consumer - pure functional programming in Scheme.

Essential steps: Start the producer The producer prepares the first iteration, and returns its first continuation via exit The consumer starts - it receives the first producer continuation Now the resume-resume interaction takes place At the end the producer sends a stop value to the consumer In the consumer, the stop value ends consumation

Program: Alternative Producer Consumer - the other coroutine is maintained in mutable state.

It is tricky to start up the two continuations Explicit passing of continuations between the coroutines is clumsy - Keeping the continuation 'of the other part' in mutable state is an alternative

Simultaneous traversal of two binary trees (1) Slide Annotated slide Contents Index References

Simulating parallel pre-order traversals of two binary trees The traversals gives rise to a list of node pairs from the two trees

Figure. Two binary trees together with the results of the simultaneous traversals

Overall approach Nodes are passed from each traversal to a controller - via (heavy) use of continuations Continuations are exchanged in between the controller and the recursive tree traversals The recursive tree traversals carry the controller continuations arround

Simultaneous traversal of two binary trees (2) Slide Annotated slide Contents Index References

Here we provide the details of the two simultaneous tree traversals

Two simulutaneous traversals scheduled by a controller: Start the controller Start pre-order traversal of the first tree - hand back pair of first node and traversal continuation Start pre-order traversal of the second tree - hand back pair of first node and traversal continuation Form pair of nodes, and recur Continue each of the traversals - hand back control continuations

Program: The basic tree functions - together with two concrete trees. Notice the constructors make-tree and leaf; The accessors root, left-tree and right-tree; and the predicates inner-node?, leaf?, and empty-tree. Even if fully within the functional paradigm, the inspiration from OOP is clear: Hide the representatinon of the tree from the application/client.

Program: The tree traversal functions.

Program: The controller function.

Program: Tree stuff, traversal, and controller - in one file.

Delayed evaluation and scheduling of a computation from an external driver Provides for interleaved excution of several functions - as controlled by the scheduler The starting point is some tail recursive functions

Program: A few functions - to be trampolined below.

(define (fact-iter n acc) (if (zero? n) acc (fact-iter (- n 1) (* acc n)))) (define (mem? n lst) (cond ((null? lst) #f) ((= (car lst ) n) #t) (else (mem? n (cdr lst))))) (define (fib n) (fib-iter n 0 0 1)) (define (fib-iter n i small large) (if (< i n) (fib-iter n (+ i 1) large (+ large small)) small)) ; > (fact-iter 5 1) ; 120 ; > (mem? 5 (list 1 2 3 4 5 6)) ; #t ; > (fib 8) ; 21

Program: Augmenting with bounce and return.

(define (return x) x) (define (bounce thunk) (call thunk)) (define (call thunk) (thunk)) (define (fact-iter n acc) (if (zero? n) (return acc) (bounce (lambda () (fact-iter (- n 1) (* acc n)))))) (define (mem? n lst) (cond ((null? lst) (return #f)) ((= (car lst ) n) (return #t)) (else (bounce (lambda () (mem? n (cdr lst))))))) (define (fib n) (fib-iter n 0 0 1)) (define (fib-iter n i small large) (if (< i n) (bounce (lambda () (fib-iter n (+ i 1) large (+ large small)))) (return small))) ; > (fact-iter 5 1) ; 120 ; > (mem? 5 (list 1 2 3 4 5 6)) ; #t ; > (fib 8) ; 21

Program: Redefining bounce and return.

(define (return x) (tag 'done x)) (define (bounce thunk) (tag 'doing thunk)) (define (tag label thing) (cons label thing)) (define (fact-iter n acc) (if (zero? n) (return acc) (bounce (lambda () (fact-iter (- n 1) (* acc n)))))) (define (mem? n lst) (cond ((null? lst) (return #f)) ((= (car lst ) n) (return #t)) (else (bounce (lambda () (mem? n (cdr lst))))))) (define (fib n) (fib-iter n 0 0 1)) (define (fib-iter n i small large) (if (< i n) (bounce (lambda () (fib-iter n (+ i 1) large (+ large small)))) (return small))) ; > (fib 8) ; (doing . #<procedure:STDIN::11935>) ; > (fact-iter 7 1) ; (doing . #<procedure:STDIN::11560>) ; > (mem? 5 (list 1 2 3 4 5 6)) ; (doing . #<procedure:STDIN::11771>)

Program: Introducing a single threaded scheduler: pogo-stick.

(define (return x) (tag 'done x)) (define (bounce thunk) (tag 'doing thunk)) (define (call thunk) (thunk)) (define (tag label thing) (cons label thing)) (define tag-of car) (define tag-value cdr) (define (pogo-stick thread) (cond ((eqv? 'done (tag-of thread)) (tag-value thread)) ((eqv? 'doing (tag-of thread)) (pogo-stick (call (tag-value thread)))))) (define (fact-iter n acc) (if (zero? n) (return acc) (bounce (lambda () (fact-iter (- n 1) (* acc n)))))) (define (mem? n lst) (cond ((null? lst) (return #f)) ((= (car lst ) n) (return #t)) (else (bounce (lambda () (mem? n (cdr lst))))))) (define (fib n) (fib-iter n 0 0 1)) (define (fib-iter n i small large) (if (< i n) (bounce (lambda () (fib-iter n (+ i 1) large (+ large small)))) (return small))) ; > (pogo-stick (fact-iter 5 1)) ; 120 ; > (pogo-stick (mem? 5 (list 1 2 3 4 5 6))) ; #t ; > (pogo-stick (fib 8)) ; 21

Exercise 3.7. Trampolining a recursive factorial function without tail calls?!

On the accompanying slide we have studied so-called trampolining of tail calls. In this exercise we will understand if/why it is necessary to apply trampolining on tail calls. Use return and bounce in a 'normal, (non-tail)recursive factorial function' fact-rec or a similar function that does not make use of tail calls. What happens if we call the function, and if we attempt to drive or schedule the computation of (fact-rec 5) with pogo-stick? Explain your findings, and draw your conclusions.

Program: Multithreaded schedulers: seesaw and trampoline.

(define (return x) (tag 'done x)) (define (bounce thunk) (tag 'doing thunk)) (define (call thunk) (thunk)) (define (tag label thing) (cons label thing)) (define tag-of car) (define tag-value cdr) (define (pogo-stick thread) (cond ((eqv? 'done (tag-of thread)) (tag-value thread)) ((eqv? 'doing (tag-of thread)) (pogo-stick (call (tag-value thread)))))) (define (seesaw thread-1 thread-2) (cond ((eqv? 'done (tag-of thread-1)) (tag-value thread-1)) ((eqv? 'doing (tag-of thread-1)) (seesaw thread-2 (call (tag-value thread-1)))))) (define (trampoline thread-queue) (let ((head (car thread-queue))) (cond ((eqv? 'done (tag-of head)) (tag-value head)) ((eqv? 'doing (tag-of head)) (trampoline (append (cdr thread-queue) (list (call (tag-value head))))))))) (define (fact-iter n acc) (if (zero? n) (return acc) (bounce (lambda () (fact-iter (- n 1) (* acc n)))))) (define (mem? n lst) (cond ((null? lst) (return #f)) ((= (car lst ) n) (return #t)) (else (bounce (lambda () (mem? n (cdr lst))))))) (define (fib n) (fib-iter n 0 0 1)) (define (fib-iter n i small large) (if (< i n) (bounce (lambda () (fib-iter n (+ i 1) large (+ large small)))) (return small))) ; > (seesaw (fact-iter 5 1) (fib 8)) ; 120 ; > (seesaw (fact-iter -1 1) (fib 8)) ; 21 ; > (trampoline (list (fact-iter -1 1) (mem? 5 (list 2 8 9 1 3 4 3 5 )) (fib 8))) ; #t

Exercise 3.7. A variant of seesaw that completes both threads

The function seesaw, as discussed on the slide, only completes one of the threads. This may be convenient in some situations (if one of the threads runs infinitly), but in general we are interested in the results of both threads. Here is the version of seesaw that we discuss: (define (seesaw thread-1 thread-2) (cond ((eqv? 'done (tag-of thread-1)) (tag-value thread-1)) ((eqv? 'doing (tag-of thread-1)) (seesaw thread-2 (call (tag-value thread-1)))))) Program a version of seesaw that - at the very end - return a list of length 2: First element must be the value finally returned by thread-1, and the second element must be the value finally returned by thread-2. Here is an example of the call of the new version of seesaw: > (seesaw (fact-iter 5 1) (fib 8)) (120 21) Your variant of seesaw may be seen as an example of a loop which maintains some state (the two threads, their status (doing/done), and their values - if they exist). As such, this exercise is a good example of programming an iterative, tail-recursive, state-transitioning function in Scheme.    Here is all you need to get started: (define (return x) (tag 'done x)) (define (bounce thunk) (tag 'doing thunk)) (define (call thunk) (thunk)) (define (tag label thing) (cons label thing)) (define tag-of car) (define tag-value cdr) (define (fact-iter n acc) (if (zero? n) (return acc) (bounce (lambda () (fact-iter (- n 1) (* acc n)))))) (define (mem? n lst) (cond ((null? lst) (return #f)) ((= (car lst ) n) (return #t)) (else (bounce (lambda () (mem? n (cdr lst))))))) (define (fib n) (fib-iter n 0 0 1)) (define (fib-iter n i small large) (if (< i n) (bounce (lambda () (fib-iter n (+ i 1) large (+ large small)))) (return small))) (define (pogo-stick thread) (cond ((eqv? 'done (tag-of thread)) (tag-value thread)) ((eqv? 'doing (tag-of thread)) (pogo-stick (call (tag-value thread)))))) ; A version of seesaw that delivers 'the value of the fastest thread'. ; The one from the video. (define (seesaw thread-1 thread-2) (cond ((eqv? 'done (tag-of thread-1)) (tag-value thread-1)) ((eqv? 'doing (tag-of thread-1)) (seesaw thread-2 (call (tag-value thread-1))))))

References The functions on this slide are inspirred from Ganz, Friedman and Wand: Trampoline Style. Wikipedia: Tail calls - through trampolining

Trampoling can be used in a compilers - for compilation of a tail-recursive function to a loop that drives the recursion

More exercises Slide Annotated slide Contents Index References

Exercise 3.9. Can you read and understand an expression with call/cc?

Take a look at this expression: (let ((x 1) (y 2) (z 3) (v 5)) (cons x (call/cc (lambda (e) (cons y (cons z (if (even? v) v (e (+ v 1))))))))) What is the value of the expression? [Needless to say: Figure it out without just putting it into your Scheme REPL.] Play with it - and try out possible variations. The same for: (let ((x 1) (y 2) (z 3) (v 5)) (+ x (call/cc (lambda (e) (+ y (+ z (if (even? v) v (e (+ v 1)))))))))

Exercise 3.9. Capturing a continuation when traversing a list

This exercises is strange! Therefore, I discourage you from making it. Most likely, you will be more confused about continuations after having made this exercise than before... Write a simple recursive function square-list that traverse a list of numbers, with the purpose of squaring each element in the list. Modify your function such that it captures a continuation of the handling of the third element in the list (if such an element exists). Replace the squared number with this continuation. Are you able to access the captured contination from the list, and demonstrate how to use it? Try this: > (define xxx (square-list (list 1 2 3 4 5 6))) > ((caddr xxx) '()) Explain your results (or lack of results). caddr is a convenient composition of car, cdr and cdr. Now try to assign the captured continuation (with set!) to a global variable remember-continuation. After you have called square-list, play with your captured and stored continuation: > (square-list (list 1 2 3 4 5 6)) > remember-continuation > (remember-continuation '()) > (remember-continuation '(10 11 12)) Discuss and explain the results you obtain.

Chapter 3: Simulation of other Paradigms and Continuations
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: August 17, 2021, 12:49:21