Kurt Nørmark
Department of Computer Science, Aalborg University, Denmark

Abstract Next lecture Index References Contents

In this lecture we first introduce the main programming paradigms. Next we introduce the functional programming paradigm using the programming language Scheme. In this lecture we cover expressions, types, lists, definitions, basic function concept, and name binding.

Lisp is the next oldest programming language - only Fortran is older.

Lisp characteristics: Invented for symbolic computations Superficially inspired by mathematical function theory Is syntactically and uniformly based on parenthesized prefix notation Parsing a Lisp program is almost trivial Programming goes hand in hand with language development It is easy to access and manipulate programs from programs Calls for tool making in Lisp Lisp is really the name of a family of languages Common Lisp, Emacs Lisp, Scheme, Clojure, ...

References Foldoc: Lisp Foldoc: prefix notation

Program: A Lisp form - A Scheme function.

(define (file-name-extension file-name) (let ((extension-pos (find-in-string-from-end file-name #\.)) (forward-slash-pos (find-in-string-from-end file-name #\/)) (backward-slash-pos (find-in-string-from-end file-name #\\))) (cond ((and extension-pos forward-slash-pos (> extension-pos forward-slash-pos)) (substring file-name (+ extension-pos 1) (string-length file-name))) ((and extension-pos forward-slash-pos (<= extension-pos forward-slash-pos)) "") ((and extension-pos backward-slash-pos (> extension-pos backward-slash-pos)) (substring file-name (+ extension-pos 1) (string-length file-name))) ((and extension-pos backward-slash-pos (<= extension-pos backward-slash-pos)) "") (extension-pos (substring file-name (+ extension-pos 1) (string-length file-name))) (else ""))))

Program = Data = Lists

Scheme Slide Annotated slide Contents Index References

Scheme is a small, yet powerful language in the Lisp family

Scheme characteristics: Supports functional programming Imperative programming is supported as well Functions are first class data objects Uses static binding of free names in procedures and functions Types are checked and handled at run time - no static type checking Parameters are evaluated before being passed - no lazyness

Scheme is an attractive alternative to Common Lisp and Emacs Lisp

References Schemers.org home page Foldoc: Scheme

Exercise 1.2. Installing a Scheme System

There are many different implementations of Scheme - Scheme Systems - around. It is important for you to install one of them, and to be able to use the installed Scheme system throughout the functional programming part of this course. It is your own choice which Scheme system you wish to use. This exercise is intended to help you, inform you about possibilities, and to locate possible software on the internet. Racket comes both with a modern and pedagogically supportive IDE - DrRacket - and a more naked Scheme engine (with a REPL - a read-eval-print loop). Racket is probably the Scheme system in most widespread use today. Earlier, Racket was known as PLT Scheme. Chez Scheme is another nice alternative. It comes as a commercial system, and as a free variant. As of now (August 2018) the commercial system has been turned in to an open-source project at github. The free variant is called Petite Chez Scheme. Direct download link for Petite Chez Scheme: for windows (version 8.4, reviewed August 2018), and for other platforms. Chez Scheme is made by the author of the book The Scheme Programming Language, Kent Dybvig. Independent of the Scheme system you use, it is recommended to develop programs in a two-pane setup. In one pane you write your Scheme source programs. In the other, you run the REPL (Read-Eval-Print-Loop) - the Scheme interpreter. There must be (will be) flexible ways to load the Scheme program (incrementally or totally) from the source pane to the REPL pane. DrRacket supports this setup. I always use Scheme from my favorite text editor, which happens to be GNU Emacs. There is a simple addition to your .emacs file which may be helpful, in case you want to program in Scheme using Emacs. When you have installed a Scheme system, be sure to give it a try. Start with some existing examples (from a possible example dir, from the text book, or from these notes). Load the Scheme forms into your REPL and evaluate them.

R5RS, R6RS, R7RS, ... Slide Annotated slide Contents Index References

Revised resports on the Algorithmic Language Scheme in various versions

Versions of Scheme: R5RS: The version on which this course is based R6RS: Much larger than R5RS R7RS: Small - finalized Big - in progress

References R5RS: The Scheme Language Report R6RS: The Scheme Language Report R7RS (Small) The Scheme Language Report

In this course our interest in Scheme is driven by the need to illustrate key concepts in functional programming Therefore R5RS compliance is sufficient for PP

The 'read-eval-print loop' allows you to interact with a Scheme system in terms of evaluation of individual expressions Some authors talk about a REPL - Read Eval Print Loop.

Program: A sample session with Scheme using a read eval print loop.

1> (+ 4 (* 5 6)) 34 2> (define x 6) 3> (+ (* 5 x x) (* 4 x) 3) 207 4> (/ 21 5) 21/5 5> (/ 21.0 5) 4.2 6> (define (fak n) (if (= n 0) 1 (* n (fak (- n 1))))) 7> (fak 50) 30414093201713378043612608166064768844377641568960512000000000000

Exercise 1.3. Testing functional programs

Tesing is important in every programming paradigm. Discuss testability of a program written in the functional paradigm, in contrast to a program written in the imperative programming paradigm. A few years ago I wrote a paper Systematic Unit Testing in a Read-eval-print Loop. You may consult this paper for your inspiration.

Practical Scheme Programming Slide Annotated slide Contents Index References

In practical use, the REPL and a Scheme source program appear in a two-pane setup

Figure. The REPL and the Scheme source editor

Types are used to make programs more readable, make them run more efficient, and to detect certain errors before they cause errors in the calculation.

Readability Explicitly typed variables, parameters and function serve as important documentation, which enhances the program understanding. Efficiency Knowledge of the properties of data makes it possible to generate more efficient code Correctness Explicit information about types in a program is a kind of redundancy against which it is possible to check expressions Programmers usually wish to identify type errors as early as possible in the development process

Reference Foldoc: type

Typing and Typecheck Slide Annotated slide Contents Index References

On this page we will provide a possible overview of different kinds of typing and typecheck There is no overall and univeral agreement on the definitions of weak/strong/static/dynamic typing

Typed/untyped Typed: Operations are only applicable to data of specified types Untyped: Any operation can be performed on any type of data Strong/weak Strong: Types are strictly enforced. Operations performed on wrong types of data leads to an error. Weak: Values of one type can be treated as values of another type Static/dynamic Static: Type checking is done before the program is executed Dynamic: Type checking is done at run-time

Scheme is (relatively) strongly and dynamically typed

References Foldoc: strong typing Foldoc: weak typing Foldoc: static typing Foldoc: dynamic typing Typing - Wikipedia

A list is recursively composed of a head and a tail, which is a (possibly empty) list itself The building blocks of lists are the cons cells Every such cell is allocated by an activation of the cons function

An illustration list construction and list selection. We first construct a list (d c b a) and we bind it to the variable lst. Next we select the first element, the tail of lst, the second element, and the second tail of lst.

Construction of the list structure which we here call x (cons e f) Selection: (car x) => e (cdr x) => f The constructor function cons takes an element e and a list f and constructs a new list. As illustrated above cons makes exactly one new cons cell, and no kind of list copying is involved at all. The selector car returns the first element of the list. A better name of car would be head . The selector cdr returns the list consisting of all but the first element in the list. A better name of cdr would be tail .

A proper list is always terminated by the empty list In Scheme the empty list is denoted '(). When we in this context talk about the termination of the list we mean the value we get by following the cdr references to the end of the list structure.

Exercise 1.4. A Proper List Predicate

The Scheme function (predicate) pair? tells if its parameter is a pair (constructed by cons). The function null? tells if its parameter is the empty list. The function list? tells if its parameter is a proper list. In this exercise, write your own version of list? Let us call our function proper-list? Intuitively, a proper list is empty, or it is 'ended by' an empty list (by following the cdr chain). You may want to read about pairs and lists in the Scheme Report. Can you write your predicate without thinking (and programming) in terms of a while loop? Can you write your predicate without using if or cond? Is your function efficient? What is the time complexity? Please - consider these questions carefully.

References R5RS: List and pair functions in Scheme Foldoc: list Foldoc: cons

Symbolic expressions and improper lists Slide Annotated slide Contents Index References

The cons function is suitable for definition of binary trees with 'data' in the leaves

Figure. A symbolic expression which illustrates the most general form it can take - a binary tree

Figure. The same symbolic expression laid out as a list. The expressions is a proper list if and only if h is the empty list. If h is not the empty list, the symbolic expression is an improper list.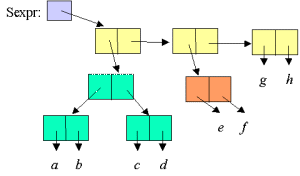

Exercise 1.5. Construction of symbolic expressions

Construct the symbolic expressions illustrated on this page via the cons primitive in Scheme. The entities named a through h should be symbols. As a help, the rightmost part of the structure is made by (cons 'g 'h) . 'g is equivalent to (quote g) , meaning that g is not evaluated, but taken for face value. Experiment with h being the empty list, which is denoted '(). Try to use a proper list function, such as length, on your structures. Can you make sense of the result?

Practical list construction Slide Annotated slide Contents Index References

cons is the basic list constructor function - but it can be applied through a number of other means as well

List and S-expression construction: Deep cons expressions Using the list function Using quote  or  quasiquote also known as backquote

Table. Examples of list construction by use of cons , list and quoted list expressions.

Expression Value (cons 1 (cons 2 (cons (+ 1 2) '()))) (1 2 3) (list 1 2 (+ 1 2)) (1 2 3) (quote (1 2 (+ 1 2))) (1 2 (+ 1 2)) '(1 2 (+ 1 2)) (1 2 (+ 1 2)) (quasiquote (1 2 (unquote (+ 1 2)))) (1 2 3) `(1 2 ,(+ 1 2)) (1 2 3)

Exercise 1.6. Every second element of a list

Write a function, every-second-element, that returns every second element of a list. As examples (every-second-element '(a b c)) => (a c) (every-second-element '(a b c d)) => (a c) Do you see any use of this function when we work with property lists? It is often worthwhile to go for a more general solution than actually needed. Therefore, program (every-nth-element n lst) where n >= 1 and lst is a proper list. Can you define every-second-element in terms of every-nth-element?

Reference R5RS: Quasiquotation

List functions Slide Annotated slide Contents Index References

There exists a number of important List functions in Scheme, and we often write other such functions ourselves We will here take a look at some of the most important list functions, as defined by the language itself. You are encouraged to read about them in the Scheme Report, to which we make a reference below.

(null? lst)     A predicate that returns whether lst is empty (list? lst)     A predicate that returns whether lst is a proper list (length lst)     Returns the number of elements in a proper list lst (append lst1 lst2)     Concatenates the elements of two or more lists (reverse lst)     Returns the elements in lst in reverse order (list-ref lst k)     Accesses element number k of the list lst (list-tail lst k)     Returns the k'th tail of the list lst And many more It should be noticed that the first element is designated as element number 0. Thus (list-ref '(a b c) 1) returns b

Reference R5RS: Pairs and Lists

Lists are passed by reference to the functions that manipulate them

Association lists Slide Annotated slide Contents Index References

An association list is a list of cons pairs Association lists are used in the same way as associative arrays

Table. Examples of association lists. The function assq uses eq? to compare the first parameter with the first element - the key element - in the pairs. As an alternative, we could use the function assoc, which uses equal? for comparison. A better and more general solution would be to pass the comparison function as parameter. Notice in this context, that both assq and assoc are 'traditional Lisp functions' and part of Scheme, as defined in the language report.

Expression Value (define computer-prefs '((peter . windows) (lars . mac) (paw . linux) (kurt . unix))) (assq 'lars computer-prefs) (lars . mac) (assq 'kurt computer-prefs) (kurt . unix) (define computer-prefs-1 (cons (cons 'lene 'windows) computer-prefs)) computer-prefs-1 ((lene . windows) (peter . windows) (lars . mac) (paw . linux) (kurt . unix))

Exercise 1.8. Creation of association lists

Program a function pair-up that constructs an association list from a list of keys and a list of values. As an example (pair-up '(a b c) (list 1 2 3)) should return ((a . 1) (b . 2) (c . 3)) Think of a reasonable solution in case the length of the key list is different from the length of the value list.

Exercise 1.8. Association lists and property lists

Association lists have been introduced at this slide. An association list is a list of keyword-value pairs (a list of cons cells). Property lists are closely related to association lists. See the slide about property lists. A property list is a 'flat list' of even length with alternating keys and values. The property list corresponding to the following association list ((a . 1) (b . 2) (c . 3)) is (a 1 b 2 c 3) Program a function that converts an association list to a property list. Next, program the function that converts a property list to an association list.

Reference Associative arrays - OOP (in Danish)

Property lists Slide Annotated slide Contents Index References

A property list is a flat, even length list of associations

Table. A comparison between association lists and property lists. In this example we associate keys (represented as symbols) to string values.

Association list Property list ((peter . "windows") (lars . "mac") (paw . "linux") (kurt . "unix")) (peter "windows" lars "mac" paw "linux" kurt "unix")

Exercise 1.9. The get-prop function for property lists

The R5RS Scheme functions assoc, assq, and assv access pairs in association lists. In this exercise we will write a similar function for property lists. More specifically, write a function get-prop with the following signature: (get-prop key property-list) The function should return the value of key in property-list. Like assoc, get-prop should return #f if key is not found in property-list. Here is an example REPL session with get-prop: > (define weekday-plist (list 'monday 1 'tuesday 2 'wednesday 3 'thursday 4 'friday 5 'saturday 6 'sunday 7)) > (get-prop 'wednesday weekday-plist) 3 > (get-prop 'sunday weekday-plist) 7 > (get-prop 'january weekday-plist) #f How will you handle the case where the property list is malformed - a property list with an odd number of elements? Discuss pros and cons of property lists and get-prop, compared to association lists and assoc. Does the #f value, returned in cases where we do not find the key, bother you?

Programs represented as lists Slide Annotated slide Contents Index References

It is a unique property of Lisp that programs are represented as data, using the main data structure of the language: the list

Program: The function from the general library that converts different kinds of data to a number.

(define (as-number x) (cond ((string? x) (string->number x)) ((number? x) x) ((char? x) (char->integer x)) ((boolean? x) (if x 1 0)) ; false -> 0, true -> 1 (else (error (string-append "Cannot convert to number " (as-string x))))

In Scheme it is not intended that the program source should be introspected by the running program. But in other Lisp systems there is easy access to this simple kind of (self) reflection.

Besides numbers, Scheme also supports booleans, characters, and symbols

Booleans True is denoted by #t and false by #f Every non-false values count as true in if and cond Characters Characters are denoted as #\a, #\b, ... Some characters have symbolic names, such as #\space, #\newline Symbols Symbols are denoted by quoting their names: 'a , 'symbol , ... Two symbols are identical in the sense of eqv? if and only if their names are spelled the same way

References R5RS: Booleans R5RS: Characters R5RS: Symbols R5RS: Equivalence predicates

Vectors Slide Annotated slide Contents Index References

Vectors in Scheme are heterogeneous array-like data structures of a fixed size

Vectors are denoted in a similar way as list Example: #(0 a (1 2 3)) Vectors must be quoted in the same way as list when their external representations are used directly The function vector is similar to the function list There are functions that convert a vector to a list and vice versa vector->list list->vector

The main differences between lists and vectors are the mode of access and the mode of construction There is direct access to the elements of a vector. List elements are accessed by traversing a chain of references. This reflects the basic differences between arrays and linked lists. The mode of construction for list is recursive, using the cons function. Lists are created incrementally: New elements can be created when needed, and prepended to the list. Vectors are allocated in one chunck, and cannot be enlarged or decreased incrementally.

References R5RS: Vectors Future exercise about binary search in vectors

Strings Slide Annotated slide Contents Index References

String is an array-like data structure of fixed size with elements of type character.

The string and vector types have many similar functions A number of functions allow lexicographic comparisons of strings: string=?, string<?, string<=?, ... There are case-independent, ci, versions of the comparison functions. The substring function extracts a substring of a string

Like lists, strings are important for many practical purposes, and it may therefore be important to familiarize yourself with the string functions in Scheme

Reference R5RS: Strings

The concept definition: A definition binds a name to a value

Syntax: A name is first introduced and the name is bound to the value of the expression

(define name expression)

About Scheme define forms Appears normally at top level in a program Creates a new location named name and binds the value of expression to that location In case the location already exists we have a redefinition, and the define form is equivalent to an assignment Does not allow for imperative programming, because define cannot appear in selections, iterations, etc. Can also appear at certain positions in bodies, but only as syntactic sugar for local binding forms (letrec)

Reference R5RS: Definitions

The conceptual starting point is the well-known mathematical concept of functions The notational starting point is lambda calculus

The mathematical function concept A mapping from a domain to a range A function transfers values from the domain to values in the range A value in the domain has at most a single corresponding value in the range Totally or partially defined functions Extensionally or intensionally defined functions Lambda calculus A very terse notation of functions and function application An extensionally defined function is defined by a set of pairs, enumerating corresponding elements in the domain and range. Notice that this causes practical problems if there are many different values in the domain of the function. An intensionally defined function is based on an algorithm that describes how to bring a value from the domain to the similar value in the range. This is a much more effective technique to definition of most the functions, we program in the functional paradigm.

Reference Foldoc: function

Evaluation of parenthesized expressions in Scheme Slide Annotated slide Contents Index References

Here we will emphasize the rules of evaluating a form like (a b c d e) in Scheme

How is the form (a b c d e) evaluated in Scheme? The form (a b c d e) appears as a pair of parentheses with a number of entities inside. The question is how the parenthesized expression is evaluated, and which constraints apply to the evaluation.

Evaluation rules The evaluation of the empty pair of parentheses ( ) is in principle an error If a is the name of a special form, such as lambda, if, cond, or define special rules apply In all other cases: Evaluate all subforms uniformly The value of a must be a function object. The function object is called with the values of b, c, d, and e as actual parameters. The evaluation of the empty pair of parentheses ( ) is often - in concrete Scheme systems - considered as the same as '( ), which returns the empty list. However, you should always quote the empty pair of parentheses to denote the empty list.

References R5RS: Procedure calls Beta Reduction - calling a function

Lambda Expressions in Scheme Slide Annotated slide Contents Index References

A lambda expression is an expression which is evaluated to a function object

Syntax:

(lambda (formal-parameter-list) expression)

Lambda expression characteristics in Scheme: No type declaration of formal parameter names Call by value parameters In reality passing of references to lists and other structures Positional and required parameters (lambda (x y z) expr) accepts exactly three parameters

Program: Simple examples of lambda expressions.

(lambda (x) ; The identity function x) (lambda (n) ; The function that adds one to a number (+ n 1)) (lambda (f) ; Given the function f, returns a function that (lambda (x) ; accepts x and applies f on x (f x)))

Lambda calculus Slide Annotated slide Contents Index References

We will here introduce the notation of the lambda calculus, mainly in order to understand the inspiration which led to the concept of lambda expressions in Lisp and Scheme.

Lambda calculus is a more dense notation than the similar Scheme notation

Table. A comparison of the notations of abstraction and combination (application) in the lambda calculus and Lisp. In some variants of lambda calculus there are more parentheses than shown here: (λ v . E). However, mathematicians tend to like ultra brief notation, and they often eliminate the parentheses. This stands as a contrast to Lisp and Scheme programmers.

Lambda calculus Scheme Abstraction λ v . E (lambda (v) E) Combination E1 E2 (E1 E2)

Reference Foldoc: lambda calculus

Lambda calculus is covered in a later PP lecture Scheme before lambda calculus

Function objects Slide Annotated slide Contents Index References

The concept function object: A function object represents a function at run time. A function object is created as the value of a lambda expression		A function object is a first class value at run time, in the same way as numbers, lists and other data are values. This is different from more traditional programming languages, where procedural and functional abstractions have another status than ordinary data.
The concept closure: A function object is also known as a closure.		The name 'closure' is related to the interpretation of free names in the body expression of the function. Free names are used, but not defined in the body. In a function object (or closure) the free names are bound in the context of the lambda expression. This is a contrast to the case where the free names are bound in the context of the application of the function.

Characteristics of function objects: First class A function object can be passed as a parameter to a function, returned as the result from another function, and organized as a constituent of a data structure Anonymous Does not have a name Closure Free names are captured in the context of the lambda expression Static binding of free names A closure is represented as a pair of the syntactical form of the function and values of free names Callable A function object can be applied on actual parameters

Functions as first class values Slide Annotated slide Contents Index References

A function object is a first class citizen

The concept first class citizen: A first class citizen is an entity which can be (1) passed as parameter to functions, (2) returned as a result from a function, and (3) organized as parts of data structures

Reference Foldoc: first class

Closures Slide Annotated slide Contents Index References

Functions capture the free names in the context of the lambda expression

An illustration of a closure, as formed by the syntactical lambda expression together with the necessary free names

Reference Function objects

More forms of lambda expressions in Scheme Slide Annotated slide Contents Index References

Syntax:

(lambda (formal-parameter-list) expression)

Syntax:

(lambda formal-parameters-name expression)

Lambda expression characteristics in Scheme: Positional and required parameters (lambda (x y z) expr) accepts exactly three parameters Required and rest parameters (lambda (x y z . r) expr) accepts three or more parameters Rest parameters only (lambda r expr) accepts an arbitrary number of parameters

Exercise 1.10. Parameter passing in Scheme

Familiarize yourself with the parameter passing rules of Scheme by trying out the following calls: ((lambda (x y z) (list x y z)) 1 2 3) ((lambda (x y z) (list x y z)) 1 2) ((lambda (x y z) (list x y z)) 1 2 3 4) ((lambda (x y z . r) (list x y z r)) 1 2 3) ((lambda (x y z . r) (list x y z r)) 1 2) ((lambda (x y z . r) (list x y z r)) 1 2 3 4) ((lambda r r) 1 2 3) ((lambda r r) 1 2) ((lambda r r) 1 2 3 4) Be sure that you can explain all the results

Function definition in Scheme Slide Annotated slide Contents Index References

A function object can be bound to a name via define like any other kind of value. But we often use a slightly different, equivalent syntax for function definitions, where the 'lambda' is implicitly specified

Syntax: The ordinary way to bind f to the value of a lambda expressions

(define f (lambda (p1 p2) ...))

Syntax: An equivalent syntactic sugaring with a more shallow parenthesis structure. Whenever Scheme identifies a list at the 'name place' in a define form, it carries out the transformation (define (f p1 p2) ...) => (define f (lambda (p1 p2) ...)) . Some Scheme programmers like the form (define (f p1 p2) ...) because the calling form (f p1 p2) is a constituent of the form (define (f p1 p2) ...)

(define (f p1 p2) ...)

The latter function definition is syntactic sugar for the first The two function definitions are identical

The concept name binding expression: A name binding expression establishes a number of local name bindings in order to ease the evaluation of a body expression

In a name binding construct a number of names are bound to values. The name bindings can be used in the body, which must be an expression when we are working in the functional paradigm. There are a number of variations in the way the names can refer to each other mutually. We will meet some of them on the following pages.

Syntax: The names n 1 ... n k are bound to the respective values e 1 ... e k , and the body expression is evaluated relative to these name bindings. Free names in the body expression are bound to names defined in the surround of the let construct.

(let ((n<sub>1</sub> e<sub>1</sub>) ... (n<sub>k</sub> e<sub>k</sub>)) body-expr)

Characteristics of a let construct: In body-expr n1 refers to the value of e1 , ..., and nk refers to the value of ek Syntactic sugar for an immediate call of a lambda expression To be illustrated on the next page As a consequence, the names are bound simultaneously relative to the name bindings in effect in the context of the let construct.

Reference R5RS: Binding Constructs (let, let*, letrec)

The equivalent meaning of let Slide Annotated slide Contents Index References

We will here understand the underlying, equivalent form of a let name binding construct

Syntax:

(let ((n<sub>1</sub> e<sub>1</sub>) ... (n<sub>k</sub> e<sub>k</sub>)) body-expr)

Syntax:

(<font color = "#0000ff" >(lambda (n<sub>1</sub> ... n<sub>k</sub>) body-expr)</font> e<sub>1</sub> ... e<sub>k</sub>)

Program: An example of an error in let.

(define seconds-in-a-day (* 24 60 60)) (define seconds-in-an-hour (* 60 60)) (define (how-many-days-hours-minutes-seconds n) (let ((days (quotient n seconds-in-a-day)) (n-rest-1 (modulo n seconds-in-a-day)) (hours (quotient n-rest-1 seconds-in-an-hour)) (n-rest-2 (modulo n-rest-1 seconds-in-an-hour)) (minutes (quotient n-rest-2 60)) (seconds (modulo n-rest-2 60)) ) (list days hours minutes seconds)))

It is now obvious that it is not possible to refer to a name ni from one of the expressions ej

The let* name binding construct Slide Annotated slide Contents Index References

It is often useful to be able to use previous name bindings in a let construct, which binds several names

Syntax:

(let* ((n<sub>1</sub> e<sub>1</sub>) ... (n<sub>i-1</sub> e<sub>i-1</sub>) (n<sub>i</sub> e<sub>i</sub>) ... (n<sub>k</sub> e<sub>k</sub>)) body-expr)

Characteristics of let*: It is possible to refer to n1 through ni-1 from the expression ei Syntactic sugar for k nested let name bindings

The let* name binding construct Slide Annotated slide Contents Index References

We show how to implement let* with let

Syntax:

(let* ((n<sub>1</sub> e<sub>1</sub>) ... (n<sub>i-1</sub> e<sub>i-1</sub>) (n<sub>i</sub> e<sub>i</sub>) ... (n<sub>k</sub> e<sub>k</sub>)) body-expr)

Syntax:

(let ((n<sub>1</sub> e<sub>1</sub>)) ... (let ((n<sub>i-1</sub> e<sub>i-1</sub>)) (let ((n<sub>i</sub> e<sub>i</sub>)) ... (let((n<sub>k</sub> e<sub>k</sub>)) body-expr))))

An example with let* Slide Annotated slide Contents Index References

Program: A typical example using sequential name binding. The task is to calculate the number of days, hours, minutes, and seconds given a number of seconds. We subsequently calculate a number of quotients and rest. While doing so we find the desired results. In this example we would not be able to use let; let* is essential because a given calculation depends on previous name bindings. The full example, including the definition of the constants, can be found in the accompanying elucidative program. The function is part of the LAML time library in lib/time.scm of the LAML distribution. The time library is used whenever we need to display time information, such as 'the time of generation' of some HTML files.

(define (how-many-days-hours-minutes-seconds n) (let* ((days (quotient n seconds-in-a-day)) (n-rest-1 (modulo n seconds-in-a-day)) (hours (quotient n-rest-1 seconds-in-an-hour)) (n-rest-2 (modulo n-rest-1 seconds-in-an-hour)) (minutes (quotient n-rest-2 60)) (seconds (modulo n-rest-2 60)) ) (list days hours minutes seconds)))

Program: A typical example using sequential name binding - all details.

(define seconds-in-a-day (* 24 60 60)) (define seconds-in-an-hour (* 60 60)) (define (how-many-days-hours-minutes-seconds n) (let* ((days (quotient n seconds-in-a-day)) (n-rest-1 (modulo n seconds-in-a-day)) (hours (quotient n-rest-1 seconds-in-an-hour)) (n-rest-2 (modulo n-rest-1 seconds-in-an-hour)) (minutes (quotient n-rest-2 60)) (seconds (modulo n-rest-2 60)) ) (list days hours minutes seconds)))

The letrec namebinding construct Slide Annotated slide Contents Index References

The letrec name binding construct allows for definition of mutually recursive functions

Syntax:

(letrec ((n<sub>1</sub> e<sub>1</sub>) ... (n<sub>k</sub> e<sub>k</sub>)) body-expr)

Program: An schematic example of a typical application of letrec for local definition of two mutually recursive functions.

(letrec ((f1 (lambda (...) ... (f2 ...))) (f2 (lambda (...) ... (f1 ...))) ) body-expr)

Characteristics of letrec Each of the name bindings have effect in the entire letrec construct, including e1 ... ek letrec can be implemented by assignments to the bound names

An implementation of letrec Slide Annotated slide Contents Index References

letrec can be implemented with use of an assignment

Syntax:

(letrec ((n<sub>1</sub> e<sub>1</sub>) ... (n<sub>k</sub> e<sub>k</sub>)) body-expr)

Syntax:

(let ((n<sub>1</sub> #f) ... (n<sub>k</sub> #f)) (set! n<sub>1</sub> e<sub>1</sub>) ... (set! n<sub>k</sub> e<sub>k</sub>) body-expr)

Binding of free names Slide Annotated slide Contents Index References

Static or dynamic binding of free names in lambda expressions

The concept free name: A name n is free in some function F if n is applied, but not defined in F

Static binding A free name n in F is bound in the (textual) context of F (in the source program) Safe and efficient The Scheme approach Dynamic binding A free name n in a function F is bound in the context of the call of F Potentially unsafe and inefficient Used in early Lisp systems - used in Emacs Lisp

Binding of free names - examples Slide Annotated slide Contents Index References

We illustrate differences between static and dynamic binding of free names

Program: A function g with four free names a, b, c, and d.

(letrec ((g (lambda () (+ a b c d))) (f (lambda (a b c d) (g)))) (f 1 2 3 4)) ; With static binding: Error: reference to undefined identifier: a ; With dynamic binding: 10

Program: A function g with four free names a, b, c, and d - statically bound in an outer let in Scheme.

(let ((a 10) (b 11) (c 12) (d 13)) (letrec ((g (lambda () (+ a b c d))) (f (lambda (a b c d) (g)))) (f 1 2 3 4))) ; With static binding: 46. The result in Scheme. ; With dynamic binding: 10. The context of *the call* of g is significant.

Program: A function g with four bounded names a, b, c, and d - passing many parameters from f to g.

(let ((a 10) (b 11) (c 12) (d 13)) (letrec ((g (lambda (a b c d) (+ a b c d))) (f (lambda (a b c d) (g a b c d)))) (f 1 2 3 4))) ; With static binding: 10. ; With dynamic binding: 10.

Dynamic binding of free name provides for implicit passing of the formal parameters of f to g In some situations, this is convenient: Temporary shadowing of more global name bindings In other situations it may give surprises...

The fluid-let namebinding construct Slide Annotated slide Contents Index References

Some Scheme systems support fluid-let, which in its body temporarily reassigns values to the names This may be used as an alternative to rebinding with use of dynamic binding.

Program: Illustration of the use of fluid-let for temporary reassignment of relatively global variables.

(let ((a 10) (b 11) (c 12) (d 13)) (letrec ((g (lambda () (+ a b c d))) ) (list (g) (fluid-let ((a 1) (b 2) (c 3) (d 4)) ; in this fluid-let a is temporarily assigned (g)) ; to 1, b to 2, c to 3, and d to 4. (g) ) ) ) ; (46 10 46)

We will illustrate the idea of referential transparency in the context of practical Scheme Programming

Program: Rewriting an expression in various ways - use of referential transparency.

(let ((a (list 1 2)) (b (list 1 2)) (c (list 3 4))) (append a b c)) <==> (let ((a (list 1 2)) (c (list 3 4))) (append a a c)) <==> (let ((a (list 1 2))) (append a a (list 3 4))) <==> (let ((a (list (- 3 2) 2)) (b (list 1 (+ 1 1)))) (append a b (list 3 4))) <==> (list 1 2 1 2 3 4)

A copy of some data can be used as a substitute for the original data A value of an expression can be used as a substitute for the expression itself A 'more complicated expression' can be used as a substitute for 'the original expression'

Referential Transparency Slide Annotated slide Contents Index References

Referential transparency is a rather fuzzy and ambiguous idea On this page we will quote and address different phrasings

Uday Reddy, Stack Overflow The term "reference" is used in analytical philosophy to talk about the thing that an expression refers to. ... A context in a sentence is "referentially transparent" if replacing a term in that context by another term that refers to the same entity doesn't alter the meaning. Stoy The only things that matters about an expression is its value, and any subexpression can be replaced by any other equal in value Wikipedia (as of August 5, 2013) An expression is said to be referentially transparent if it can be replaced with its value without changing the behavior of a program Landin (a) each expression has a nesting subexpression structure, (b) each subexpression denotes something (usually a number, truth value or numerical function), (c) the thing an expression denotes, i.e., its "value", depends only on the values of its sub-expressions, not on other properties of them. Bird and Wadler The value of an expression depends only on the values of its constituent expressions (if any) and these subexpressions may be replaced freely by others possessing the same value Stack Overflow, Brian Bondy Referential transparency ... means that given a function and an input value, you will always receive the same output. KN In a given context, two expressions that are equal to each other may substitute each other

Reference Referential Transparency, Stack Overflow

More Excercises Slide Annotated slide Contents Index References

Exercise 1.16. A calendar language - Some calendar functions

Design a small Lisp language (in Scheme) for calendars and appointments. A calendar can contain a number of appointments. An appointment is characterized by an appointment text, a starting time and an ending time. Times have the usual constituents: Year, month, day, hour, and minute. A calendar can also contain other calendars recursively (as in a Composite design pattern). In addition to the design of the Lisp Calendar language, you are requested to write a number of processing functions, including a function that presents a calendar in HTML. In this assignment we distinguish between: A calendar expression, which makes use of a number of constructor functions (for the calendar as such, for each appointment, for starting time, ending time, etc). Each such construction function should accept flexible parameters, and it should check its constituents such that a constructed calendar/appointment is guaranteed to be well-formed. The constructor functions should return an internal representation (see below). There must be functions that access the parts of a calendar, the parts of an appointment, the parts of a time, etc. An internal representation, as generated by the constructor functions. Feel free pick an internal representation which fits your needs and preferences. You may prefer to think of the internal representation as an abstract syntax tree of the calendar language. Please, in particular, consider how to represent time in your calendar. The internal representation may reflect the calendar expressions rather directly, or it may reorganize the calendar in a way which fits the operational needs (see below). One or more external presentations. In this assignment we will produce a simple HTML presentation of the calendar (see below). You are asked to program the following functionality on calendars and appointments: Functions that add and delete appointments/calendars to and from the calendar. Feel free to the design the signatures of theses functions appropriately. Please be sure to program pure functions (which return a new calendar that represents the addition/deletion). (present-calendar-html cal from-time to-time) A function that presents the appointments of a calendar within a given time interval: From a calendar start time from-time to a calendar end time to-time. The function must return an HTML value (such as a text string that represents an HTML fragment). You decide the organization (daily, weekly, monthly, ...) of the resulting calendar. You are encouraged to isolate concrete HTML details in a specific layer of Scheme functions. (In other words, try to avoid that HTML details and string concatenations are spread throughout all corners of the function present-calendar-html). (find-appointments cal pred) Find and return the list of all appointments in the calendar cal that fulfills the appointment predicate pred. (find-first-appointment cal pred) Find the earliest appointment (if any) that satisfies the appointment predicate pred. Return #f if no such appointment exists in the calendar. (find-last-appointment cal pred) As find-first-appointment, but find the latest appointment instead of the earliest. (flatten-calendar cal) A function that eliminates nested calendars. All appointments of nested calendards must be raised to appointments in the top-level calendar. The function should return the flattened calendar. (appointments-overlap? ap1 ap2) A predicate that returns if the two appointments ap1 and ap2 overlap in time. Please notice that two appointments can be overlapping in several different ways. (calendars-overlap? cal1 cal2) A predicate that returns if two calendars have one or more overlapping appointments. If this functions returns false (#f), all appointments in the two calendars are temporally disjoint. In case of inaccuracies in the formulations of this exercise, please state the conditions under which you have created you solution.

Exercise 1.16. A counterpart to list-tail

The Scheme function list-tail returns the n'th tail of a list: > (list-tail '(a b c d e) 2) (c d e) > (list-tail '(a b c d e) 0) (a b c d e) > (list-tail '(a b c d e) 4) (e) Program your own version of list-tail. Call it my-list-tail. Next, program a function list-prefix which is a prefix counterpart to list-tail. (list-prefix lst n) returns a prefix of the list of length n: > (list-prefix '(a b c d e) 2) (a b) > (list-prefix '(a b c d e) 4) (a b c d) > (list-prefix '(a b c d e) 0) () Do not just use reverse and/or length in clever ways. Make 'a real implementation' of list-prefix. Reflect on the difference between these two functions. Which one is most expensive in terms of memory allocation?

Exercise 1.16. The function butlast

R5RS has functions such that list-ref and list-tail. (list-ref lst n) returns element number n in a list, (list-tail lst k) returns a suffix of list (omitting k elements). In this exercise we will program a function butlast. (butlast lst) returns all elements of lst apart from the last element. Thus, butlast computes the prefix of the list consisting of all elements but the last one. Needless to say, butlast assumes as a precondition that the input list is non-empty. Let us notice that it is harder to compute the prefix of a list than a suffix of a list. Why? The following implementation of butlast is tempting, but inefficient (quick and dirty): (define (butlast lst) (reverse (cdr (reverse lst))))) Now, program butlast with a single traversal of the list. Can you generalize butlast to compute the prefix of a list appart from the last n elements: (define (but-n-last lst n) ...)) Please consider the similarity between but-n-last and list-prefix from one of the other exercises.

Exercise 1.16. Lexicographic photo file naming

Imagine that we have a collection of photo files, named arbitrarily. We also have a list of photo file names (or photo path names) which represents a desired order of the photos. In this exercise we wish to copy the collection of photos to a new destination. At the new destination, the photo files must be renamed lexicographically, relative to the given list of photo names. By that we mean that the name of the first photo file should be "AAA", the next "AAB", the twenty sixth "AAZ", the twenty senventh "ABA", and the last "ZZZ". With this kind of naming, most photo playing devices will show the photos in the desired order (because it will sort the photos alphabetically before showing them). In the scenario above we have used names of three characters. The number of digits can/should be adopted to the number of photo files. In addition we have used the alphabet of capital letters from 'A' to 'Z'. Other alphabets may, of course, be possible. Write a function (next_photo_name current-photo-name) which returns the name after current-photo-name, in lexicographic order. Thus, for example (next_photo_name "A") => "B" (next_photo_name "AA") => "AB" (next_photo_name "AAAZ") => "AABA" (next_photo_name "HIJK") => "HIJL" Make a wise decision about the value of (next_photo_name "ZZZ"). Your function next_photo_name should be recursive. The function is simple in case the last letter in the string is lower than the last letter in the alphabet. A recursive solution is used if the last letter in the string is equal to the last letter of the alphabet. For test purposes, write a function (list-of-photo-names first-name n) that generates a list of n photo names, each with the same number of letters as in first-name. As an example (list-of-photo-names "AAA" (* 26 26 26)) should generate the full list of all 17576 three letter photo file names from "AAA" to "ZZZ". Given the functions next-photo-name and list-of-photo-names it is relatively simple to plug it into a useful file copy function, such as this function: (define (copy-photos! source-photo-name-list target-photo-name-list source-path destination-path) (for-each (lambda (source-photo-name target-photo-name) (let* ((source (string-append source-path source-photo-name)) (destination (string-append destination-path target-photo-name)) ) (if (not (file-exists? destination)) (copy-file source destination) (display-message "Destination file exists" destination "- NO copy made.")) ) ) source-photo-name-list target-photo-name-list)) (copy-photos! some-photo-list (list-of-photo-names "AAA" (length some-photo-list)) ...) Notice that this function is imperative, a named accordingly (with an exclamation suffix in the function name). Notice also the use of file-exists?, copy-file and display-message (all of which are non R5RS procedures). In the sketch above we assume that a three-letter file length will be appropriate.

Exercise 1.16. A music language in Scheme

Design a simple and small Lisp (Scheme) language for music. In this assignment, music is basically modelled in terms of notes and pauses. A note is characterized by a pitch value, a duration, and an instrument. A pause is characterized by a duration. A pitch value is an integer between 0 and 127 (where 60 is middle C). Durations are integers; 960 time units correspond roughly to a second. Instruments are represented as symbols, where the following are supported: Piano, Organ, Guitar, Violin, Flute, Trumpet, Helicopter eller Telephone. Notes and pauses can be composed sequentially and in parallel. Conceptually, a MusicElement is either a Note, a Pause, a SequentialMusicElement or a ParallelMusicElement. A SequentialMusicElement represents a collection of MusicElements which are played in a strict sequence (one after the other). A ParallelMusicElement represents a collection of MusicElements which are played together (all starting at the same time). Please notice the recursive nature of this modelling: A SequentialMusicElement or a ParallelMusicElement consist of parts, which themselves may be of type SequentialMusicElement and/or ParallelMusicElement. Notes and pauses terminate the recursion. This model of music is a composite (design pattern), and it can be illustrated as in the following class hierarchy: 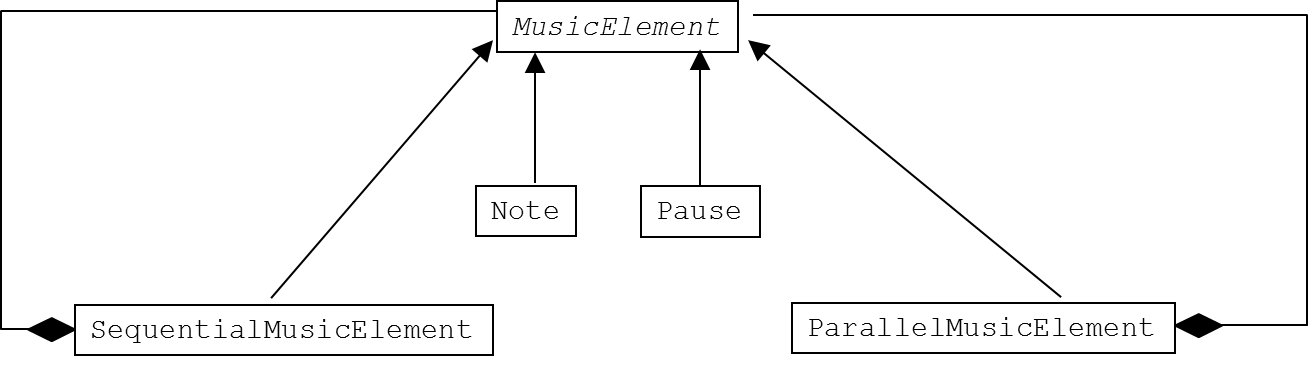You are asked to program the following functionality: Constructor functions for the Scheme Music Language - one for each of the four forms of music elements. Each such construction function should accept flexible parameters, and it should check its constituents such that a constructed music element is guaranteed to be well-formed. Music elements may be constructed in terms of the pich values, duration values and instrument values. Alternatively, or supplementary, you may prefer to introduce note names (such as C, CS, D), durations in terms of rational numbers (such as 1/2, 1/4, 1/8), octave numbers, and similar ideas. Predicates that identify each of the four music elements. Selectors that access the parts of each type of a music element. Functions that scales, transposes, and re-instruments a music element. Scaling multiplies durations with a scaling factor, transposition adds to the note pitch, and re-instrumentation changes instrument. Each of these must be implemented as pure functions that return modified music elements. A function that returns the duration of music element. A boolean function monophonic? that returns if a music element is monophonic (at most one note sounds at a time) An integer function degree-of-polyphony that returns the maxium number of notes that play at the same time in a music element. Please notice: The degree of polyphony of a parallel music element may be less than the count of its constituent music elements (due to pauses in some parts). Therefore you should be careful when you program degree-of-polyphony for ParallelMusicElements. A function that maps (linearizes) a music element object to a flat list of absolutely time note objects (a list which we conceive as a low level "event list"). Absolutely timed note objects can be constructed by the function note-abs-time-with-duration (already provided and implemented for you). A list of note-abs-time-with-duration forms can be transformed to a playable MIDI file in a number of different ways (see below). Finally, your program must include an example of a simple canon song, and you must include the generated MIDI file in your submission. The constructor function note-abs-time-with-duration takes the following parameters: (note-abs-time-with-duration abs-time channel note-number velocity duration) where abs-time: A non-negative integer, in time ticks. The absolute start time of the note. channel: An integer between 1 and 16, which in reality is a MIDI channel allocated to the requested instrument. Channel 1 is a piano, channel 2 is an organ, channel 3 is a guitar, channel 4 is a violin, channel 5 is a flute, channel 6 is a trumpet, channel 7 is a helicopter, and channel 8 is a telephone. note-number: An integer between 0 and 127. In reality a MIDI note number. velocity: An integer between 0 and 127. The velocity (strength) of the note. Not controllable in this exercise. Therefore it can be given as a constant, such as 80. duration: A non-negative integer. The duration of this note (measured in time ticks). The procedure transform-to-midi-file! transforms a list of note-abs-time-with-duration forms to a playable MIDI file. The procedure has the following signature: (transform-to-midi-file-and-write-to-file! low-level-event-list filename) where low-level-event-list: A list of values, each of which are returned by the function note-abs-time-with-duration. filename: A MIDI file name, or a path to MIDI file name. The low-level transformation functionality, which supports this exercise, can be downloaded from the course website in a number of different variants (depending on your Scheme platform). Alternatively, a playable MIDI file can be generated by a web service from a list of note-abs-time-with-duration forms, provided that you use this simple implementation of the constructor function: ; Construct the low-level internal representation of a note (with note-number) ; bound to a particular absolute time (in time ticks), and with a given duration ; (in time ticks). The channel parameter encodes the instrument used. ; The velocity represents the strengths of the node. (define (note-abs-time-with-duration abs-time channel note-number velocity duration) (cons 'note-abs-time-with-duration (list abs-time channel note-number velocity duration))) In case of inaccuracies in the formulation of this exercise, please state the conditions under which you have created you solution.

Exercise 1.16. AAU group formation

In this exercise we will work with the concepts student, group and grouping. The overall purpose is to program various ways to make project groups, in the context of PBL group work at AAU. A student has the following properties: Student-id, name, sex, ethnicity (country born), and age. The student-id is unique, and it corresponds directly to the AAU student number (represented as a string). The sex is either "male" or "female" (both strings). The nationality is a string (such as "Danish"). The age is a non-negative integer. As such, a student can be represented by various list formats, as a struct, or as a simulated OOP object. A group is a set of students, which, for some purpose, belongs together (such as in a semester group at AAU). The group also has a group-id, which in this exercise is an integer group number (starting from 1). A group can be represented as the group-id together with a list of students, or (shorter) a group-id together with a list of student-ids. A grouping attaches a group to each student in our population of interest. Thus, in a grouping each student should belong to exactly one group. A grouping can be represented as a list of groups. Alternatively, a grouping can be represented as an association list which maps student-ids to group-ids. In this exercise, we recommend that a grouping is represented as an association list, which associcates a group number to a student. As an example, the association list (ordered arbitrarly): ((1 . a) (1 . e) (2 . b) (1 . c) (2 . d)) defines a grouping consting of two group. Group 1 consists of the students a, e and c. Group 2 consists of the students b and d. The starting point of this exercise is a population of n students. There exists a sample population of 200 students, which can be used as the starting point in a solution to this exercise. You are supposed to input/read these student in the beginning of your program. Write a function that returns a given group from a grouping. In addition, write a function that returns the number of groups in the grouping, a function that return the maximum group size in a grouping, and a function that returns the minimum group size in a grouping. Write constructor, predidate, selection functions for a single student. As part of this you must decide how to represent a student in your program. Write a constructor function for a single group, and write a group predicate function. In addition, write a selector function that returns a list of students in the group, and a selector function that returns the group-id (group number). Both the constructor and selectors will most likely be trivial, but it is good for us to have these functions available. The various grouping functions (discussed below) will serve as grouping constructor functions. Write a predicate that identifies a grouping object. For practical purposes it is recommended to program (pretty)printing functions for students, groups and groupings. Random grouping: Given a list of students sl and a list of desired group sizes gsl, program a grouping function that forms (length gsl) groups, of the sizes prescribed in gsl. This grouping function should return a grouping. The function should asserts that gsl is a list on positive integers (g1 g2 ... gk), where g1+g2+...+gk = (length sl). The grouping should be recursive, in a straightforward way: Initially, form a group of g1 students (randomly selected with use of a random function), and solve the remaining random grouping problem recursively, for the group size list (g2 ... gk). Grouping by counting: Program a second grouping function which mimics the "manual couting approach" to the formation of k groups. In this approach, the grouping relies somehow on the order of students in the student collection. The counting goes: 1, 2, ..., k, 1, 2, ... k, ... (a total of n times where n is the number of students). This leads to a marking of each student by the allocated group number, and based on the marking, a grouping object should be created. Balanced grouping by counting: As a variant of grouping by counting, program a third grouping function to form k groups from the n students which ensures equal distribution of sex and equal distribution of ethnicality in the constructed groups. As equal as possible in the real world. Please come up with a good, pragmatic and reasonable solution. Random grouping with group predicate. As a variant of random grouping, add a group predicate to the parameter list of grouping function. Do your best to form groups that fulfill the group predicate. If a (random) group is formed, which breaks the group predicate, redo the random pick of the group (up to a limit, such as 1000 times). Program and play with the following group predicates: At least N students in a group are A years old, or older. All students in the group are female. No students in the group are of the same age. In the 2020 version of the PP1 miniproject, the Random grouping with group predicate is considered as optional. It is allowed to use a non-pure random function function for random grouping (such as random in Racket). In addition, you are allowed to write non-pure print functions. All other functions in your solution should be pure functions.

Chapter 1: Introduction to Functional Programming in Scheme
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: August 13, 2021, 14:51:36