


   | Rekursion |
Ligesom Fibonacci tal er Towers of Hanoi en absolut klassiker i diskussion og introduktion af rekursion.
Towers of Hanoi illustrerer en beregningsmæssig opgave med eksponentiel køretid. Derved ligner dette program vores første program til beregning af Fibonacci tal (afsnit 34.2). Ligheden rækker dog ikke langt. Det var helt enkelt at finde en effektiv algoritme til udvikling af talrækken af Fibonacci tal. Der er ingen genveje til løsning af Towers of Hanoi problemet.
|
36.1. Towers of Hanoi (1)
Indhold Op Forrige Næste Slide Aggregerede slides Stikord Programindeks Opgaveindeks
Problemet bag Towers of Hanoi er at flytte skiver fra et tårn til en anden med en tredje som 'mellemstation'. De nærmere regler er beskrevet herunder.
Towers of Hanoi er en gammel asiatisk overlevering om munke, der skulle flytte 64 skiver fra én søjle til en anden Ifølge legenden ville templet og verden omkring det falde inden arbejdet kunne fuldføres |
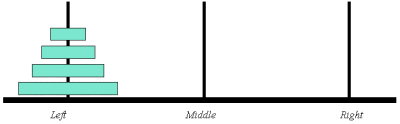
| Figur 36.1 En illustration af Towers of Hanoi med fire skiver. |
|
36.2. Towers of Hanoi (3)
Indhold Op Forrige Næste Slide Aggregerede slides Stikord Programindeks Opgaveindeks
Vi løser Towers of Hanoi problemet ved udpræget brug af en del og hersk strategi, jf. afsnit 11.6. Delproblemerne appellerer til rekursiv problemløsning, idet delproblemerne til forveksling ligner det oprindelige problem.
Vi programmerer en løsning på problemet som kun viser hvilke flytninger der skal foretages. Bogen har en løsning, som også viser hvordan tårnene ser ud efter hver flytning. |
Funktionen hanoi herunder flytter n skiver fra tårn a til tårn b med brug af tårn c som mellemstation. Som det fremgår af program 36.2 er typen tower en enumeration type som dækker over værdierne left, middle og right. Enumerationtyper blev behandlet i afsnit 18.3.
1 2 3 4 5 6 7 8 9 10 | /* Move n discs from tower a to tower b via tower c */
void hanoi(int n, tower a, tower b, tower c){
if (n == 1)
move_one_disc(a,b);
else {
hanoi(n-1,a,c,b);
move_one_disc(a,b);
hanoi(n-1,c,b,a);
}
} | |||
|
Lad os nu forstå løsningen i program 36.1. Hvis n er lig med 1 er løsningen triviel. Vi flytter blot skiven fra tårn a til b. Dette gøres med move_one_disc. Hvis n er større end 1 flyttes først n-1 skiver fra a til hjælpetårnet c (det første røde sted). Dernæst flyttes den nederste store skive fra a til b med move_one_disc (det andet blå sted). Endelig flyttes de n-1 skiver på fra c til b, nu med a som hjælpetårn (det andet røde sted).
Hele programmet er vist i program 36.2. Vi ser først enumeration typen tower og dernæst hanoi funktionen beskrevet herover. Funktionen move_one_disc rapporterer blot flytningen ved at udskrive data om flytning på standard output (skærmen). Variablen count, som er static i funktionen (jf. afsnit 20.3), tæller antallet af flytninger, blot for at tilfredsstille vores nysgerrighed om opgavens omfang. Funktionen tower_out, som kaldes fra move_one_disc, løser problemet med at udskrive en tower værdi. Denne problematik er tidligere illustreret i bl.a. program 18.7. Funktionen main prompter brugeren for antallet af skiver, og dernæst kaldes hanoi.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | #include <stdio.h>
enum tower {left, middle, right};
typedef enum tower tower;
void move_one_disc(tower a, tower b);
char *tower_out(tower t);
/* Move n discs from tower a to tower b via tower c */
void hanoi(int n, tower a, tower b, tower c){
if (n == 1)
move_one_disc(a,b);
else {
hanoi(n-1,a,c,b);
move_one_disc(a,b);
hanoi(n-1,c,b,a);
}
}
void move_one_disc(tower a, tower b){
static long count = 0;
count++;
printf("%5i. Move disc from %6s tower to %6s tower\n",
count, tower_out(a), tower_out(b));
}
char *tower_out(tower t){
static char *result;
switch (t){
case left: result = "LEFT"; break;
case middle: result = "MIDDLE"; break;
case right: result = "RIGHT"; break;
}
return result;
}
int main(void) {
int number_of_discs;
printf("How many discs: ");
scanf("%d", &number_of_discs);
hanoi(number_of_discs, left, right, middle);
return 0;
} | |||
|
En kørsel af program 36.2 med fire skiver giver følgende output:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 1. Move disc from LEFT tower to MIDDLE tower
2. Move disc from LEFT tower to RIGHT tower
3. Move disc from MIDDLE tower to RIGHT tower
4. Move disc from LEFT tower to MIDDLE tower
5. Move disc from RIGHT tower to LEFT tower
6. Move disc from RIGHT tower to MIDDLE tower
7. Move disc from LEFT tower to MIDDLE tower
8. Move disc from LEFT tower to RIGHT tower
9. Move disc from MIDDLE tower to RIGHT tower
10. Move disc from MIDDLE tower to LEFT tower
11. Move disc from RIGHT tower to LEFT tower
12. Move disc from MIDDLE tower to RIGHT tower
13. Move disc from LEFT tower to MIDDLE tower
14. Move disc from LEFT tower to RIGHT tower
15. Move disc from MIDDLE tower to RIGHT tower | |||
|
Som det tydeligt fremgår af næste afsnit, vil outputtet fra program 36.2 føles som uendelig langt hvis hanoi kaldes med et stort heltal n som input.
36.3. Towers of Hanoi (4)
Indhold Op Forrige Næste Slide Aggregerede slides Stikord Programindeks Opgaveindeks
Som allerede observeret forårsager hvert ikke-trivielt kald af hanoi to yderligere kald. Derved fordobles arbejdet for hver ekstra skive, som er involveret. Dette er eksponentiel vækst.
Det er let at se at antallet af flytninger F(n) vokser eksponentielt med antallet af diske i tårnet. Mere præcist ser vi at F(n) = 2 n - 1. |
Vi kan kun håndtere et arbejde, som vokser eksponentielt, for meget begrænsede problemstørrelser. I tabel 36.1 illustreres dette konkret. I søjlen 10-9 antager vi at vi kan flytte 1000000000 skiver pr. sekund. I søjlen 10-3 antager vi at vi kun kan flytte 1000 skiver pr. sekund. Uanset dette ser vi at arbejdet tager tilnærmelsesvis uendelig lang tid at udføre, når n går mod 100.
| n | 2n | 10-9 · 2n | 10-3 · 2n |
| 5 | 32 | 3.2 · 10-8 sek | 3.2 · 10-2 sek |
| 25 | 3.4 · 107 | 0.03 sek | 9.3 timer |
| 50 | 1.1 · 1015 | 13 dage | 35702 år |
| 65 | 3.7 · 1019 | 1170 år | 1.17 · 109 år |
| 80 | 1.2 · 1024 | 3.8 · 107 år | 3.8 · 1013 år |
| 100 | 1.2 · 1039 | 4.0 · 1013 år | 4.0 · 1020 år |
| Tabel 36.1 En table der viser antallet af flytninger og køretider af hanoi funktionen. Køretiderne i tredje kolonne er angivet under antagelsen af vi kan flytte 109 skiver pr. sekund. Køretiderne i fjerde kolonne er angivet under antagelsen af vi kan flytte 103 skiver pr. sekund. |