


   | Funktioner |
Vi gennemgår her et lidt mere avanceret eksempel, nemlig rodsøgning i en kontinuert funktion. Vores primære interesse er naturligvis problemløsning og funktioner, herunder topdown udvikling og programmering ved trinvis forfinelse.
|
13.1. Rodsøgning (1)
Indhold Op Forrige Næste Slide Aggregerede slides Stikord Programindeks Opgaveindeks
Vi starter med den essentielle observation, der danner baggrund for den centrale rodsøgningsalgoritme:
Enhver kontinuert funktion f, som har en negativ værdi i l og en positiv værdi i u (eller omvendt) vil have mindst én rod r mellem l og u. |
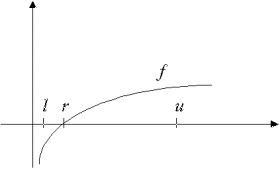
| Figur 13.1 En kontinuert funktion f med en rod mellem l og u |
I figur 13.1 ser vi tydeligt at der skal være mindst én rod mellem l og u, nemlig i r. Der kan sagtens være flere rødder. Hvis dette er tilfældet har vi ingen egentlig kontrol over, hvilken af disse vi finder.
Ved at indsnævre intervallet [l, u], og ved hele tiden at holde roden mellem l og u, kan vi hurtigt finde frem til
en værdi r for hvilken f(r) = 0. |
13.2. Rodsøgning (2)
Indhold Op Forrige Næste Slide Aggregerede slides Stikord Programindeks Opgaveindeks
Den central algoritme, som finder en rod mellem l og u er vist i program 13.1. Bemærk, at vi forudsætter at l er mindre end (eller lig med) u, og at fortegnet af funktionens værdi i l og u er forskellige. Med andre ord skal situationen være som i figur figur 13.1.
1 2 3 4 5 6 7 8 9 | double findRootBetween(double l, double u){
while (!isSmallNumber(f(middleOf(l,u)))){
if(sameSign(f(middleOf(l,u)), f(u)))
u = middleOf(l,u);
else
l = middleOf(l,u);
}
return middleOf(l,u);
} | |||
|
I programmet flytter vi gentagne gange enten l eller u til midtpunktet . Bemærk her, at l og u er parametrene i funktionen findRootBetween, og når vi ændrer på l eller u er det kun den lokale værdi i funktionen der ændres. Dette er en konsekvens af brug af værdiparametre (se afsnit 12.7).
De røde, blå og lilla dele af findRootBetween i program 13.1 skal nu programmeres. I alle tre tilfælde er der tale om småfunktioner, der medvirker til at højne abstraktionsniveauet i findRootBetween. I program 13.2 viser vi mulige definitionen af disse funktioner.
1 2 3 4 5 6 7 8 9 10 11 | int sameSign(double x, double y){
return x * y >= 0.0;
}
double middleOf(double x, double y){
return x + (y - x)/2;
}
int isSmallNumber(double x){
return (fabs(x) < 0.0000001);
} | |||
|
Vi kan nu samle alle dele i ét program. Alternativt kunne vi have organiseret 'stumperne' i to eller flere kildefiler, ligesom vi gjorde i tændstikpige eksemplet i afsnit 11.5.
Vi bemærker, at vi i main programmerer en løkke, som gentagne gange beder brugeren af programmet om intervaller, hvor vi søger efter rødder i funktionen x3 - x2 - 41 x + 105. Som antydet ved vi at der er rødder i 5.0, 3.0 og -7.0. Det skyldes at x3 - x2 - 41 x + 105 faktisk bare er lig med (x - 5.0) . (x - 3.0) . (x + 7.0). Prøvekør selv programmet, og find rødderne!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | #include <stdio.h>
#include <math.h>
double f (double x){
/* (x - 5.0) * (x - 3.0) * (x + 7.0) */
return (x*x*x - x*x - 41.0 * x + 105.0);
}
int sameSign(double x, double y){
return x * y >= 0.0;
}
double middleOf(double x, double y){
return x + (y - x)/2;
}
int isSmallNumber(double x){
return (fabs(x) < 0.0000001);
}
double findRootBetween(double l, double u){
while (!isSmallNumber(f(middleOf(l,u)))){
if(sameSign(f(middleOf(l,u)), f(u)))
u = middleOf(l,u);
else
l = middleOf(l,u);
}
return middleOf(l,u);
}
int main (void){
double x, y;
int numbers;
do{
printf("%s","Find a ROOT between which numbers: ");
numbers = scanf("%lf%lf", &x, &y);
if (numbers == 2 && !sameSign(f(x),f(y))){
double solution = findRootBetween(x,y);
printf("\nThere is a root in %lf\n", solution);
}
else if (numbers == 2 && sameSign(f(x),f(y)))
printf("\nf must have different signs in %lf and %lf\n",
x, y);
else if (numbers != 2)
printf("\nBye\n\n");
}
while (numbers == 2);
} | |||
|