Primula supports the parameter learning technique for Relational Bayesian Networks described in this ICML 07 paper. The method is based on likelihood maximization using gradient ascent, and can be applied to complex models containing nested and non-decomposable combination functions. For example, the model nested_combfunc.rbn contains a nested application of the combination functions noisy-or and exponential sum (esum) where the latter is non-decomposable, and defined as esum(p1,...,pn)=exp(-sum_i pi). In this model, the probability that the probabilistic relation r(v) is true for a node v in a colored graph depends on the distribution of blue nodes two edges away: the probability for the attribute r for the bottom node in this small tree-structured graph
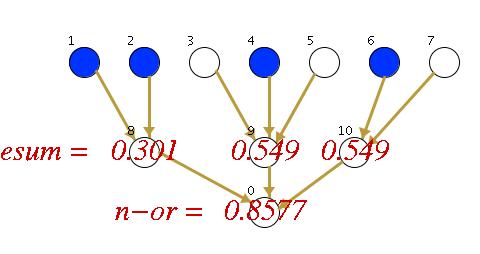
is computed by first evaluating the inner esum combination function for all nodes one edge away. This gives the values exp(- k * 0.6), where k is the number of blue neighbors one further edge away. These esum values are then combined by a noisy-or, giving the probability value 0.8577.
The model nested_combfunc.rbn contains two parameters: the weight a blue neighbor adds to the inner esum function (=0.6), and the weight a non-blue neighbor adds to the inner esum function (=0). Using Primula's Learn Module these parameters can be learned from data.