Kurt Nørmark ©
Department of Computer Science, Aalborg University, Denmark


September 2001

Abstract Previous lecture Next lecture Index References Contents

I denne lektion tager vi udgangspunkt i en meget vigtig kvalitet ved software, nemlig korrekthed. Vi stiller os selv spørgsmålet: 'korrekt i forhold til hvad'? Svaret på spørgsmålet er korrekthed i forhold til en specifikation. Vi ser på forskellige muligheder for at specificere et program, og vi vælger at koncentrere os om brugen af logiske udtryk i termer af pre- og postbetingelser. Ud over specifikationsproblemet ser vi også på problemstillingen omkring ansvarsfordeling. I et stort program er der meget vundet ved at være bevidst og eksplicit om fordelingen af ansvar mellem forskellige dele af programmet. Disse dele er helt naturligt objekter og operationer i det objekt-orienterede paradigme. Under behandlingen af ansvarsfordeling læner vi os op ad en god metafor, nemlig kontraktbegrebet, som vi ofte støder på i vores hverdag. Det viser sig at kontraktbegrebet - og subkontrakter - kan forklare væsentlige aspekter af nedarvningsmekanismen. Dette ser vi naturligvis på. Vi slutter af med forskellige praktiske spin off effekter af de foregående ideer, såsom kontraktovervågning (i forhold til programbeviser) samt undtagelseshåndtering.

En software kvalitet er en positive egenskab, som vi ønsker at tilføre et program

Table. En række kvaliteter ved software, deres beskrivelse, og som kontrast, deres modsætning. Kvaliteter er positivt ladede ord.

Kvalitet Beskrivelse Modsætning Korrekthed Opfyldelse af intentionen Ukorrekthed Robusthed Modståelig over for uventede situationer Skrøbelighed Genbrugelighed Kan bruges i andre sammenhænge Anvendelsesspecifik Enkelhed Undgår indviklede løsninger Komplekst Forståelighed Mental håndterbarhed af programmet Uforståelighed ............. ................. .........

Korrekthed Slide Note Contents Index References Speak

Korrekthed er den oplagte softwarekvalitet. Her udfordrer vi hinanden på, hvad vi egentlig forstår ved korrekthed

Vi ønsker at skrive korrekte programmer Korrekte i forhold til hvad?

Korrekthed kan være relativ til programmørens forståelse Ofte uformuleret og flygtig en formuleret specifikation Formel eller uformel Separat eller en del af programmet

Specifikation Slide Note Contents Index References Speak

Specifikation går forud for implementation. Vi kan opfatte specifikation som en del af designfasen. Her ser vi på forskellige aspekter af specifikationer

The concept specifikation: En program specifikation er en eksakt forskrift som skal opfyldes af program implementationen En specifikation besvarer 'hvad spørgsmål' i modsætning til 'hvordan spørgsmål'

En specifikation beskriver og foreskriver egenskaberne af en efterfølgende program implementation. Ideelt beskæftiger en specifikation sig med 'hvad' et program skal gøre, ikke noget om 'hvordan' det skal ske

Formelle teknikker til specifikation af abstrakte datatyper: Algebraisk specifikation. En mængde af ligninger som angiver de kaldsmæssige egenskaber af datatypens operationer i forhold til et antal særlige konstruktorer Axiomatisk specifikation. En mængde af logiske udsagn om de definitionsmæssige egenskaber af datatypen og dens operationer Algebraisk specifikation er en elegant teknik, som tillader os at specificere abstrakte datatyper. Kerneideen er en angivelse af, hvordan de forskellige operationer (funktioner) virker på såkaldte konstruktorer (også funktioner) I denne lektion vil vi koncentrere os om axiomatiske specifikationer

Program: Et eksempel på en algebraisk specifikation af en stak. Øverst ser vi en syntaktisk definition af signaturerne af de operationer, som virker på en stak. Alle operationer skal være funktioner. Nederst ses den semantiske specifikation af stakken. Princippet er at vise hvordan de forskellige stakfunktioner virker på konstruktorerne, som er new og push.

Type stack [int] declare constructors new () -> stack; push (int, stack) -> stack; destructors pop (stack) -> stack; selectors top (stack) -> int; empty (stack) -> bool; for all i in int; s in stack; let pop (new()) = error; pop (push (i,s)) = s; top (new()) = error; top (push (i,s)) = i; empty (new()) = true; empty (push(i,s)) = false; end end stack.

Program: Et eksempel på en axiomatisk specifikation af en kvadratrodsfunktion.

sqrt(x: Real) -> Real precondition: x >= 0; postcondition: abs(result * result - x) <= 0.000001

The concept logisk udtryk: Et logisk udtryk er et udtryk af typen boolean		'Logiske udtryk' er betegnelsen for den delmængde af udtryk som beregnes til et boolsk resultat (altså true eller false resultat). Et logisk udtryk kaldes også ofte for et udsagn
The concept prebetingelse: En prebetingelse af en operation er et logisk udtryk, som skal være opfyldt umiddelbart før operationen kaldes		En prebetingelse er et udsagn om situationen før kaldet af en operation. I prebetingelsen er der mulighed og behov for at referere til operationens parametre
The concept postbetingelse: En postbetingelse af en operationer et logisk udtryk, som skal være opfyldt umiddelbart efter at operation er udført		En postbetingelse er et udsagn om situationen efter kaldet af operationen. Hvis operationen er en procedure karakteriserer postbetingelsen programtilstanden efter operationskaldet. Hvis operationen er en funktion beskriver postbetingelsen resultatet (output) i forhold til parametrene (input)

Prebetingelse En prebetingelse udtrykker, om det er meningsfyldt at kalde operationen med de givne parametre Prebetingelsen's opfyldelse er en forudsætning for at operationen kan kaldes Postbetingelse En postbetingelse udtrykker at operationen returnerer et bestemt resultat eller har en bestemt effekt, når denne kaldes med de givne parametre som opfylder prebetingelsen Postbetingelsen fastlægger betydningen af operationen

Logiske udtryk kaldes ofte for assertions på engelsk og udsagn på dansk

Eksempel på brug af pre- og postbetingelser i et objekt-orienteret program Slide Note Contents Index References Speak

Vi har talt om pre- og postbetingelser i forhold til operationer. I objekt-orienteret programmering hører operationerne til i klasser. Vi går nu over til at studere pre- og postbetingelser af operationer i en klasse. Vi ser indledningsvist på et konkret eksempel

En version af CircularList hvor der er en øvre grænse på størrelsen af listen

Program: Klassen CircularList med pre- og postbetingelser. Alle andre detaljer er ignoreret. Prebetingelser angives med nøgleordet require og postbetingelse med nøgleordet ensure. Denne syntaks stammer direkte fra Eiffel. Bemærk venligst at programmet ikke er programmeret i Java, idet Java ikke understøtter require og ensure. Vi antager at countElement er en operation som rent faktisk tæller antallet af elementer i Listen. Endvidere at prædikaterne isFirst og isLast er funktioner, der fortæller hvorvidt et element er det første hhv. det sidste element i listen. Vi benytter også funktionerne retrieveSecond og retrieveButLast til returnering af hhv. listens andet og næstsidste element. Bemærk specielt udtryksformen old og noChange. Old foran et udtryk i postbetingelsen beregner udtrykket i den programtilstand der var gældende umiddelbart før kaldet af operationen. NoChange er opfyldt, hvis operationen ikke har ændret programtilstanden. (NoChange er med andre ord opfyldt, hvis operationen er en funktion). Old og NoChange giver kun mening i postbetingelser.

class CircularList { /** Construct an empty circular list */ public CircularList() require true; ensure empty(); /** Return my number of elements */ public int size() require true; ensure size = countElements() && noChange; /** Insert el as a new first element */ public void insertFirst(Object el) require !full(); ensure !empty() && isCircular() && isFirst(el); /** Insert el as a new last element */ public void insertLast(Object el) require !full(); ensure !empty() && isCircular() && isLast(el); /** Delete my first element */ public void deleteFirst() require !empty(); ensure empty() || (isCircular() && isFirst(old retrieveSecond())); /** Delete my last element */ public void deleteLast() require !empty(); ensure empty() || (isCircular() && isLast(old retrieveButLast())); /** Return the first element in the list */ Object retrieveFirst() require !empty(); ensure isFirst(result) && noChange; /** Return the last element in the list */ Object retrieveLast() require !empty(); ensure isLast(result) && noChange; }

Exercise 9.1. Pre- og postbetingelser i CircularList

På den tilknyttede slide er der vist pre- og postbetingelser for klassen CircularList. I betingelserne anvendes funktionerne empty(), countElements(), isCircular(), isFirst(Object), isLast(Object), retrieveSecond() og retrieveButLast(). Denne opgave går ud på at implementere ovennævnte funktioner som private operationer i klassen CircularList. Simuler pre- og postbetingelserne ved at kalde funktionerne hhv. først og sidst i klassen's metoder. Hvis der brydes en prebetingelse skal man udføre: throw new PreconditionBroken() Tilsvarende skal et brud af en postbetingelse føre til udførelse af: throw new PostconditionBroken() Download filen med min løsning af opgaven om Cirkulære lister. Denne fil indeholder endvidere de nødvendige erklæringer af de ovenfor nævnte exception klasser. Udtrykkene i 'old ...' kan volde særlige problemer. Ideen med old er at kunne evaluere et udtryk i den programtilstand som bestod netop inden metoden blev kaldt. Derfor vil det være en mulighed at forudberegne disse 'old udtryk' i starten af metoden.

Et sprog til formulering af 'assertions' Slide Note Contents Index References Speak

Hvis vi ønsker at behandle assertions formelt skal der naturligvis eksistere et sprog, hvori assertions kan formuleres

Vi ønsker at inkludere en specifikation i termer af pre- og postbetingelser i et program Vi må have et delsprog af programmeringssproget, i hvilket vi kan formulere 'assertions' i et program Vi ønsker at kunne efterchecke udsagn i et kørende program

Et muligt specifikationssprog Understøttelse af simple, logiske udtryk (med and, or, not, implies) Brug af alkvantorer ('for alle ...') og eksistenskvantorer ('der eksisterer ...') Det er problematisk at efterchecke udtryk med kvantorer i et kørende program Understøttelse af programmerede assertions via boolske funktioner i programmeringssproget Problematisk hvis der er fejl i disse Understøttelse af uformelt formulerede udsagn i programkommentarer Langt bedre end ingen specifikation Egenskaberne af et muligt specifikationsssprog er direkte inspireret af det objekt-orienterede programmeringssprog Eiffel Årsagen til, at kvantorer er problematisk, er udtryk for er ønsket om at kunne efterchecke assertions i et kørende program. Hvis vi ønsker 'kvantorudtryksform' kan vi falde tilbage på at programmere boolske funktioner, som returnerer hvorvidt 'alle ... opfylder en betingelse' eller 'om der eksisterer ... der opfylder en betinglse' Programmerede udsagn er problematiske derved, at specifikationen ikke ønskes afhængiggjort af programmet. Hvad skal vi f.eks. stille op med specifikationen af de programmerede udsagn; og hvad hvis der er fejl i disse dele af programmet?

De fleste klasser i et objekt-orienteret program forvalter et bestemt ansvar Med 'ansvarsfordeling' interesserer vi os bl.a. for hvorledes vi kan undgå overlappende ansvar mellem klasserne og ansvarsforflygtigelse.

Generelt om ansvarsfordeling Uden en klar fordeling af ansvar vil der være en tendens til at alle dele af et program påtager sig et stort ansvar at alle dele af et program checker for alle mulige betingelser (defensiv programmering) at gøre et stort program større og mere kompleks Med en klar fordeling af ansvar opnår vi at operationerne i et program kan operere i forhold til ganske bestemte forudsætninger minimale mængder af check af mulige fejlbetingelser positivt bidrag i retning af et mere enkle programmer

Det overansvarlige program Slide Note Contents Index References Speak

For at skabe en kontrast til vores videre diskussion af ansvarsfordeling vil vi se på et program, hvor de enkelte dele (klasser) påtager sig et for stort ansvar.

Figure. Et eksempel på et program med overlappende ansvarsforvaltning. Programmet er en karikatur af et overansvarligt program. Vi ser flere eksempler på at både klient og Kontoklassen tester for de samme forhold. Endvidere er kontoklassen designet ud fra en overansvarligheds filosofi; Hvis man hæver et negativt beløb 'får man det bedste ud af situationen' ved nemligt at indsætte det tilsvarende positive beløb. Det tilsvarende gør sig gældende hvis man indsætter et negativt beløb

Exercise 9.2. Kontrakter i Bankkonto

Denne opgave handler igen om én af vore favoriteksempler, nemlig klassen Konto. Ved øvelserne i lektion 3 blev der stillet en opgave om at repræsentere en Konto med en transaktionshistorie. Brug løsningen på den tidligere opgave hvis I har behov for at hente et passende udgangspunkt for denne opgave. Forsyn klassen konto med en kontrakt. Mere specifikt: Lav pre- og postbetingelser på alle operationer i klassen Definer en klasseinvariant Vær specielt opmærksom på invarianten, som skal sikre konsistens mellem datarepræsentationen (transaktionshistorien) og de eksterne egenskaber af kontoen. (Man kan iøvrigt hente meget konkret inspiration til denne opgave i artiklen 'Applying Design by Contract').

Det ansvarsløse program Slide Note Contents Index References Speak

Som en kontrast til programmet på forrige side viser vi her 'det ansvarsløse program.

Figure. En kontrast til det overansvarlige program. Vi har blot strippet programmet for al overansvarlighed. Dette viser, hvor store mængder af program der skal vedligeholdes, hvis vi ønsker at gå med både livrem, seler, og hvad man nu ellers går rundt med for at holde bukserne oppe...

Ansvarsfordeling specificeret med pre- og postbetingelser Slide Note Contents Index References Speak

Vi fastlægger nu hvordan man kan bruge pre- og postbetingelser til at definere en ansvarsfordeling mellem klienter og forsyner objekter. I forhold til det overansvarlige program, som blev diskuteret ovenfor, trækker vi nogle tests (betingelser) ud af programmet til fordel for en placering i specifikationen. Pre- og postbetingelser, som bliver brudt, er udtryk for meget alvorlige fejl, som for de fleste programmer bør være fatale. Altså, hvis en pre- eller postbetingelser bliver brudt, giver det ikke mening at fortsætte programudførelsen

Pre- og postbetingelser kan bruges til at specificere ansvarsfordelingen mellem klasser og operationer i et objekt-orienteret program

Opfyldelse af pretingelsen Kalderen's ansvar Klienten's ansvar i et objekt-orienteret program Opfyldelse af postbetingelsen Den kaldte operation's ansvar Forsyneren's ansvar i et objekt-orienteret program

Kontraktbegrebet Slide Note Contents Index References Speak

Vi introducerer nu kontraktbegrebet for software, som en metafor i forhold til kontrakter kendt fra vores hverdag. Vi omgås alle med mange forskellige kontrakter. Eksempelvis indgår vi i et kontrakt-lignende forhold med vores forsikringsselskab; kontrakten udtrykker gensidige forpligtigelser hvis der opstår en skade. Hvis vi køber en bil skriver vi under på en kontrakt med bilforhandleren om leveringsbetingelser mv. Hvis vi optager et lån i en bank indgår der en kontrakt. Der er også talrige kontrakter i spil i forhold til offentlige myndigheder, som oftest er påtvungen os ved lov.

Pre- og postbetingelserne af operationer i en klasse udgør tilsammen en kontrakt mellem klassen og dens klienter

The concept kontrakt: En kontrakt udtrykker de gensidige forpligtelser mellem to dele af et program, som samarbejder om løsningen af et problem

En kontrakt mellem to dele af et program svarer til kontrakt begrebet som vi kender det fra den virkelige verden. Her er altså tale om en gensidig forpligtigelser mellem to parter, som har indgået en aftale. Ifølge Nudansk ordbog er en kontrakt en 'bindende skriftlig overenskomst'. Ordbogen eksemplificerer dette med leje-, engagement-, eller købssituationer.

Et kontraktbrud er en alvorlig begivenhed som bringer programmet i en undtagelsestilstand, som for det meste vil afstedkomme at programmet stopper udførelsen Et kontraktbrud opfattes som en fejl i programmet i forhold til specifikationen Vi kan også sige, at kontraktbrud opfattes som en fatal fejl i programmet, som er udtryk for et brud på specifikationen

Kontrakter: ydelse og nydelse Slide Note Contents Index References Speak

En kontrakt indebærer som regel både fordele og forpligtelser. Vi benytter her de lidt poppede, men ganske sigende betegnelser 'ydelse' og 'nydelse'

Figure. Figuren udtrykker at der både er forpligtelser (ydelser) og lettelser (nydelser) når man indgår en kontrakt. Vi viser her nydelse og ydelse i forhold til en forsyner klasse og en klient klasse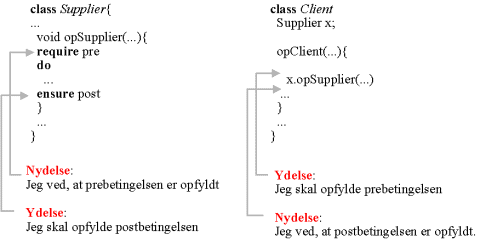

En operation i klassen lover at opfylde post-betingelsen såfremt klienten kalder operationen med opfyldt prebetingelse. Kontrakten er udtryk for en klar ansvarsfordeling mellem klient og leverandøren. Det er klientens ansvar at undersøge, om prebetingelsen af supplier-operationen er opfyldt. Hvis dette ikke er tilfældet, bliver supplier-operationen ikke kaldt, og der opstår en fejlsituation i klienten. Det er således ikke nødvendigt i kroppen af en operation i leverandør-klassen at teste, om operationens pre-betingelse er opfyldt. Den skal være opfyldt. Hvis supplier-operationen ikke opfylder sin post-betingelse opstår der en fejlsituation i supplier klassen. Denne klare ansvarsfordeling, og deraf følgende minimale, test af betingelser forud for udførelsen af en operation, står i skarp kontrast til defensiv programmering. Som vi har omtalt går man i defensiv programmering både med livrem og seler i den forstand, at man gerne udfører samme test (f.eks. prebetingelsen) to forskellige steder i programmet, for at forhindre misforståelser om ansvarsfordelingen. I og med at opfyldelse af prebetingelsen er klientens ansvar, skal alle dele af en prebetingelse være tilgængelig for klienterne.

Ydelse og nydelse i kvadratrods funktionen Slide Note Contents Index References Speak

For at konsolidere forståelseen af idéen om ydelse og nydelse i forbindelse med kontrakter viser vi her i specifikationen af kvadratrodsfunktionen hvad der ydelse og hvad der er nydelse

Kvadratrod(x: Real) -> Real require x >= 0; ensure result * result = x;

Table. Ydelse og nydelse i kvadratrodsfunktionen. Klienten er kalderen af funktionen. Forsyneren er selve funktionen.

- Ydelse Nydelse Klient Skal overføre et ikke negativt tal x Får returneret kvadratroden af input'et Forsyner Returnerer y, hvorom der gælder at y * y = x Skal ikke bekymre sig om negative input

Klasseinvarianten udtrykker nogle krav, som skal være opfyldt på ethvert stabilt tidspunkt i levetiden af klassens instanser

The concept klasseinvariant: En klasseinvariant udtrykker egenskaber af et objekt, som er uforanderlige i forhold til en række påvirkninger af objektet

En invariant er en egenskab som er uforanderlig når et objekt (eller lignende) bliver udsat for en række påvirkninger

En klasseinvariant virker som en generel skærpelse af både pre- og postbetingelser af metoder klassen kan benyttes til at udtrykke nogle generelle konsistensforhold mellem metoder og/eller datarepræsentation udgør et 'sundhedskriterium' for instanser af klassen

Eksempel. Der skal altid være én kop kaffe på kanden

Invarianter kendes også fra vores ikke-tekniske hverdag. Det er f.eks. en regel, at kanden på afdelingens kaffemaskiner altid skal indeholde mindst én krus kaffe. Alle transaktioner på kaffemaskinen skal overholde denne invariant. Bemærk at handlingerne, der beståer i at tømme kaffekanden samt at lave ny kaffe er at betragte som én transaktion i denne model. På et tidspunkt er kanden tom, men da dette tidspunkt ikke forekommer mellem to (eksterne) transaktioner på maskinen, bryder vi ikke invarianten.

 

Exercise 9.3. Klasseinvariant i DoubleLinkable

Vi har i en tidligere lektion studeret dobbeltkædede lister. Se her for den relevante slide. Formuler en passende klasseinvariant for en dobbeltkædet liste, som udtrykker at dobbeltkædningen er i orden. Skitser et prædikat (boolsk funktion) på klassen DoubleLinkable, som udtrykker at et enkelt led i kæden er 'i orden'.

Eksempel på klasseinvariant: CircularList Slide Note Contents Index References Speak

Lad os her se på et konkret eksempel på benyttelse af klasseinvarianter. Det er naturligt at vende tilbage til det eksempel, som vi studerede lidt tidligere omkring pre- og postbetingelser

Program: Klassen CircularList med en invariant. Bemærk at flere af pre- og postbetingelserne er blevet simplere end vist ovenfor. Dette hænger sammen med at klasseinvarianten skærper alle pre- og postbetingelser

class CircularList { /** Construct an empty circular list */ public CircularList() require true; ensure empty(); /** Return my number of elements */ public int size() require true; ensure (size = countElements) && noChange; /** Insert el as a new first element */ public void insertFirst(Object el) require !full(); ensure !empty() && isFirst(el); /** Insert el as a new last element */ public void insertLast(Object el) require !full(); ensure !empty() && isLast(el); /** Delete my first element */ public void deleteFirst() require !empty(); ensure (empty() || isFirst(old retrieveSecond)); /** Delete my last element */ public void deleteLast() require !empty(); ensure (empty() || isLast(old retrieveButLast())); /** Return the first element in the list */ Object retrieveFirst() require !empty(); ensure isFirst(result) && noChange; /** Return the last element in the list */ Object retrieveLast() require !empty(); ensure isLast(result) && noChange; invariant !empty() implies isCircular() and empty() implies (size() = 0); }

Reference Pre- og postbetingelser i cirkulær liste

Hvornår skal en invariant være opfyldt? Slide Note Contents Index References Speak

Vi beskrev løst ovenfor, at en invariant skal være opfyldt på ethvert stabilt tidspunkt i et objekts levetid. Vi vil nu gør dette udsagn væsentligt mere præcist

En klasseinvariant skal opfyldes på følgende tidspunkter i et objekts levetid: Umiddelbart efter objektets skabelse (initialisering via en konstruktor) Før udførelsen af en offentlig operation Efter udførelsen af en offentlig operation Vi ser, at klasseinvarianten er et 'sigtepunkt' for konstruktorerne i en klasse. Objekter skal starte livet et en sund tilstand. De sunde tilstande af et objekt beskrives af klassens klasseinvariant

Klasseinvarianten skal ikke nødvendigvis opfyldes efter udførelse af private operationer i klassen En privat operation spiller ofte rollen som en hjælpeoperation. Udførelse af en sådan hjælpeoperation bringer ikke nødvendigvis objektet i en sund tilstand. Der skal muligvis flere påvirkninger til inden objektet havner i en tilstand, hvor klasseinvarianten gælder

Figure. Problemstillingen omkring forholdet mellem assertions når en klasse B arver fra klassen A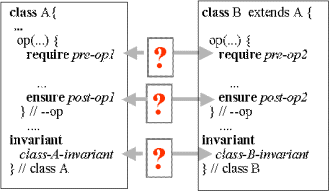

Hvordan forholder assertions i en subklasse sig til de tilsvarende assertions i en superklasse?

Subkontrakter Slide Note Contents Index References Speak

Vi har indset at mængden af assertions (pre- og postbetingelser samt invarianten) på en klasse C kan opfattes som en kontrakt. Vi vil nu studere hvordan denne kontrakt udvikler sig når vi danner subklasser af klassen C

Via polymorfi kan subklasser 'gøre det ud for' superklasser Derfor skal subklasser's kontrakter overholde kontrakten defineret af en superklasse Subklassers kontrakter skal udgøre en subkontrakt af superklassens kontrakt

Assertions i en subklasse Prebetingelser må ikke strammes Postbetingelser må ikke svækkes Klasseinvarianter må ikke svækkes En operation i en specialiseret klasse må ikke forhindre et kald af sig selv, som er garanteret af superklassens tilsvarende operation. Derfor må prebetingelsen ikke strammes En operation i en specialiseret klasse skal gøre arbejdet mindst lige så godt som den tilsvarende operation i superklasenklasse. Derfor må postbetingelsen ikke svækkes

Operationer kan ikke redefineres 'på må og få' i et klassehierarki Reglerne ovenfor formaliserer, at operationerne der redefineres ned gennem et specialiseringshierarki, skal være tæt beslægtede - også semantisk. Hidtil har vi kun set lagt bånd på navne og parametre af redefinerede operationer (covarians). Her kommer vi altså med nogle semantiske forventninger (krav) i forbindelse med redefintion. Dette er meget tilfredsstillende

Eksempel på klasseinvarianter: Trekantshierarkiet Slide Note Contents Index References Speak

Vi har tidligere studeret hierarkiet af trekanter. Først nu hvor vi er bevæbnet med klasseinvarianter kan vi på en tilfredsstillende måde karakterisere specialiseringen i dette klassehierarki

Figure. Invarianter i klassehierarkiet af trekanter: Generel trekant: 3 sider og 3 vinkler Vinkelsum er 180 grader Ligebenet trekant: Invariant generel trekant To sider er lige lange Retvinklet trekant: Invariant-generel Phytagoras Ligesidet trekant: Invariant-ligebenet Tredie side har samme længde som de to andre Retvinklet ligebenet trekant: 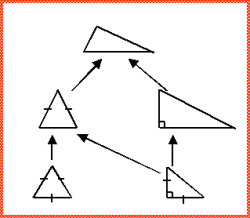Invariant-retvinklet Invariant-ligebenet

I takt med at vi specialiserer trekanterne styrkes klasseinvarianterne

Assertions i abstrakte klasser Slide Note Contents Index References Speak

Assertions giver i høj grad mening i abstrakte klasser. Via reglerne for redefinerede operationers assertions er det meget nyttigt at angive assertions allerede på et meget generelt niveau i et klassehierarki

Det er nyttigt og meningsfyldt at definere kontrakter i abstrakte klasser

Program: Den abstrakte klasse Stack forsynet med assertions. Vi har taget udgangspunkt i den abstrakte klasse Stack fra forrige lektion. Pre- og postbetingelser i "..." er uformelle, kommentarlignende udsagn, som ikke vil kunne eftercheckes når programmet kører.

abstract class Stack{ abstract public void push(Object el) require !full; ensure !empty && top() = el && size() = old size() + 1; abstract public void pop(); require !empty(); ensure !full() && size() = old size() - 1; abstract public Object top() require !empty(); abstract public boolean full() ensure "size() = capacitet"; abstract public boolean empty() ensure size() = 0; abstract public int size() ensure "result = number of elements on stack"; public void toggleTop(){ require size() >= 2; Object topEl1 = top(); pop(); Object topEl2 = top(); pop(); push(topEl1); push(topEl2); ensure size() = old size() && "top and element below top are exchanged"; } // toggleTop public String toString(){ return("Stack"); } }

Reference Klassen Stack

Definition af abstrakte klasser med kontrakter understøtter specifikation i form af 'design by contract' Abstrakte klasser er i overvejende grad udtryk for design, som kontrast til implementation. Når vi forsyner abstrakte klasser med kontrakter vil vi tale om 'design by contract'

Undervejs i et programudførelse kan assertions checkes i forhold til programmets aktuelle tilstand

Assertions er udtryk for redundans, og assertions kan som sådan anvendes til check. I lidt mere jævnt sprog kan vi sige, at assertions er et supplerende element i vore programmer i forhold til 'det der sker i operationerne'; Assertions beskriver programmets handlinger på højere og logisk niveau. Vi kan sammenligne det der faktisk sker når vi kører med programmet med det, der er udtrykt i vore assertions.

Brud på en kontrakt bringer programudførelsen i store vanskeligheder Under programtest leder dette til debugging og fejlrettelse Under programdrift bringer dette programmet i en undtagelsessituation som bør føre til kontrolleret nedlukning eller valg af en alternativ programudførelsesstrategi Når eller hvis der opdages et brud på en kontrakt, f.eks. en invariant som ikke holder når man kører programmet, har vi identificeret et stort problem. Det giver ikke mening at fortsætte programudførelsen. Der kan være tale om en programmeringsfejl i forhold til specifikationen af programmet. I en debugging situation er det eneste fornuftige at få rettet denne fejl. I en driftssituation har vi identificeret en undtagelsessituation, som typisk håndteres ved en kontrolleret nedlukning af programmet. I nogle meget kritiske programmer vil vi ønske at genoptage programudførelsen med en ændret 'beregningsstrategi' (recovery).

Udbyttet af kontrakter i programudviklings processen Slide Note Contents Index References Speak

Vi vil her opsummere udbyttet af kontrakter og assertions i hele programudviklingsprocessen

Kontrakter bidrager på følgende måde i programudviklingens faser - og videre frem: Design: En pragmatisk fornuftig måde at lave programspecifikation Dokumentation: Udgør sammen med signaturer og kommentarer et væsentlig del af klassens dokumentation Implementation: Udgør retningslinier for programmeringen Verifikation: Grundlaget for et formelt bevis af programmets korrekhed Test: Afslører brud på kontrakter og deraf følgende behov for debugging og fejlretning Drift: Bringer programmet i en undtagelsestilstand som udfordrer dets robusthed Når vi taler om dokumentation i forbindelse med kontrakter tænker vi på, at kontraktforhold vil være meget nyttige at dokumentere via javadoc genereret dokumentation

Kontraktidéen går på tværs af alle væsentlige kontruktive faser i en programudviklingsproces

Assertions i objekt-orienterede programmeringssprog Slide Note Contents Index References Speak

Eiffel er et objekt-orienterede programmeringssprog som understøtter assertions. Den primære inspirationskilde til materialet i dette afsnit er således Bertrand Meyer, som har lavet Eiffel

Idéerne i denne lektion understøttes direkte i det objekt-orienterede programmeringssprog Eiffel Eiffel er designet af Bertrand Meyer, som også er forfatter til artiklen 'Applying Design by Contract'

Assertions og kontrakter i andre objekt-orienterede sprog Simulere ideerne ved brug af boolske funktioner Understøttes ved anvendelse af en preprocessor Angives ved brug af kommentarer

I Java er der desværre ingen understøttelse af kontrakter og assertions Der findes dog flere forsøg på at påklistre assertions og kontrakter til Java via præ-processorer

References Eiffel hjemmeside Mini artikel om kontrakter og assertions Jass - Java with assertions

Assertions finder anvendelse i andre sammenhænge end kontrakter Løkkeinvarianter er en primær 'mekanisme' som tillader os at styre og ræsonnere om en løkke

Program: Et eksempel på en iterativ funktion med en løkke invariant.

static int div(int x, int y){ // require x > 0 && y > 0; int rest = x; int quotient = 0; while (rest >= y) { // invariant rest + quotient * y = x; // System.out.println(rest + quotient * y == x); rest = rest - y; quotient = quotient + 1; } return (quotient); // ensure rest + quotient * y = x && rest < y && rest >= 0; } // end div

Collected references Contents Index

Pre- og postbetingelser i cirkulær liste Klassen Stack Jass - Java with assertions Mini artikel om kontrakter og assertions Eiffel hjemmeside

Chapter 9: Designkontrakter og ansvarsfordeling
Course home     Author home     About producing this web     Previous lecture (top)     Next lecture (top)     Previous lecture (bund)     Next lecture (bund)     
Generated: March 31, 2008, 12:09:01