Kurt Nørmark
Institut for Datalogi, Aalborg Universitet
| Sammendrag Forrige lektion Næste lektion Stikord Referencer Indhold | I denne lektion gennemgår vi funktions- og procedure begrebet, herunder lokale variable og parametre. Vi ser naturligvis også på detaljer omkring funktioner i C. |
| Procedurer og funktioner uden parametre |
| Procedurer og Funktioner Slide Indhold Stikord Referencer |
|
| Begrebet abstraktion: En abstraktion indkapsler, navngiver og parametriserer en samling af programdetaljer | ||
| Begrebet procedure: En procedure er en abstraktion over en sekvens af kommandoer | ||
| Begrebet funktion: En funktion er en abstraktion over et udtryk |
|
| Program: Illustration of grundlæggende karakteristika af procedurer og funktioner - vist i C. |
|
| Program: Samme program - uden brug af funktioner og procedurer. |
|
|
| Funktionsdefinition uden parametre i C Slide Indhold Stikord Referencer |
|
| Syntax: En funktionsdefinition i C |
|
|
|
| Kald af en funktion uden parametre Slide Indhold Stikord Referencer |
| Syntax: Et funktionskald i C |
|
|
| Program: Illustration af funktionsdefinition efter funktionskald. |
|
| Program: Funktionsdefinition før funktionskald. |
|
| Program: Løsning af 'definition efter kald' med brug af en prototype. |
|
| Eksempel: Rødder i en andengradsligning Slide Indhold Stikord Referencer |
|
|
| Program: Et program der finder rødder i en andengradsligning - uden funktioner - alt i main. |
|
| Program: En funktion der finder rødder i en andengradsligning. |
|
|
|
|
| Lokale variable Slide Indhold Stikord Referencer |
|
|
| Program: Illustration af ulovlig anvendelse af en lokal variabel. |
|
| Top-down programmering ved trinvis forfinelse |
| Lasagne al forno Slide Indhold Stikord Referencer |
|
|
| Struktureret lasagne Slide Indhold Stikord Referencer |
|
| Program: Ustruktureret lasagne. |
|
| Program: Struktureret Lasagne. |
|
| Program: Lav en portion lasagneplader. |
|
| Program: Lav en portion hvid sovs. |
|
| Program: Lav en portion kødsovs. |
|
|
| Lasagne ala C Slide Indhold Stikord Referencer |
|
| Program: Et pseudo C program som laver lasagne. |
|
| Program: Et pseudo C program som laver lasagne - funktioner med parametre. |
|
| En tændstikpige (1) Slide Indhold Stikord Referencer |
|
| Program: Det ønskede output - tændstikpigen. |
|
| Program: Udskrivning af tændstikpige i termer af udskrivning af hoved, arme, krop og ben. |
|
|
| En tændstikpige (2) Slide Indhold Stikord Referencer |
|
| Program: Udskrivning af hoved, arme, krop og ben i termer af generelle geometriske figurer. |
|
|
| En tændstikpige (3) Slide Indhold Stikord Referencer |
|
| Program: Udskrivning af cirkler, linier og andre geometriske figurer. |
|
| En tændstikpige (4) Slide Indhold Stikord Referencer |
|
| Figur. En illustration of problemer og delproblemer i forbindelse med tegning af en tændstikpige |  |
| En tændstikpige (5) Slide Indhold Stikord Referencer |
|
| Program: Tændstikpige programmet. |
|
| Program: Filen char-graphics.h - header fil med prototyper af de grafiske funktioner. |
|
| Program: Filen char-graphics.c - implementationen af de grafiske funktioner. |
|
| Program: Oversættelse af programmerne. |
|
| Program: Oversættelse af programmerne - med mange warnings. |
|
| Program: Makefile - som automatiserer oversættelsen. |
|
| Program: Makefile med makroer. |
|
|
|
| Del og hersk - del og kombiner Slide Indhold Stikord Referencer |
|
| Figur. Opdelning af et kompleks problem i delproblemer | 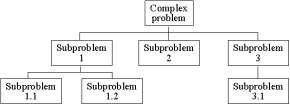 |
|
| C funktioner med input parametre |
| Formelle og aktuelle parametre Slide Indhold Stikord Referencer |
|
| Syntax: En funktionsdefinition i C |
|
|
| Syntax: Et funktionskald i C |
|
| Program: Illustration af formelle og aktuelle parametre. |
|
|
|
| Eksempel: Rødder i en andengradsligning Slide Indhold Stikord Referencer |
|
|
| Program: En funktion der finder rødder i en andengradsligning - nu med input parametre. |
|
|
|
|
| Opgave 5.2. Trinvis forfinelse af solveQuadraticEquation | På mange måder er funktionen solveQuadraticEquation fra programmet på den tilhørende slide en god løsning på at finde rødderne i den generelle andengradsligning a x2 + b x + c = 0. Dog udestår, som omtalt på tilhørende slide, en tilfredsstillende løsning på aflevering af outputtet: Antallet af rødder og rødderne selv. Men det kommer lidt senere i kurset. I denne opgave vil vi nedbryde problemløsningen endnu mere, og vi vil på systematisk vis programmere C funktioner som løser disse delproblemer. Målet med opgaven er altså primært på at anvende ideerne om trinvis forfinelse og top-down programmering. Dette indebærer delmål om programmering af funktioner med inputparametre, brug af prototyper af funktioner, og brug af return til formidling af output fra en funktion. Programmer hvert af følgende delproblemer som en separat funktion:
Hvis der kun er én rod, anses første og anden rod for at være ens. Hvis der ikke findes rødder må de to sidstenævnte funktioner ikke kaldes. Find gode navne til funktionerne, der løser ovenstående tre delproblemer, og forsyn funktionerne med relevante input parametre. Funktionernes output skal formidles via funktionernes returværdi. Omskriv programmet så det kalder de tre funktioner. Vær sikker på at du bibeholder funktionen solveQuadraticEquation. Programmer endvidere main således at solveQuadraticEquation kaldes i en løkke. I denne løkke skal de tre koeficienter a, b og c indlæses. Afslut løkken når alle de tre indlæste koeficienter a, b og c er lig med 0. Dette kan gøres med en sentinel-controlled loop. Løs ligningen (inden i løkken) i de tilfælde, hvor det giver mening. Vær sikker på at du organiserer dit C program ud fra de anbefalinger vi har set om top-down programmering ved trinvis forfinelse. I denne opgave bedes du programmere det hele i én C fil. Der skal således ikke laves en header fil med prototyper. |
| Eksempel: Temperaturomregninger Slide Indhold Stikord Referencer |
|
| Program: Et program som omregner frysepunkt og kogepunkt til Fahrenheit grader - uden abstraktion. |
|
| Program: Et program som omregner frysepunkt og kogepunkt til Fahrenheit grader. |
|
| Figur. To kald af fahrenheit_temperature funktionen | 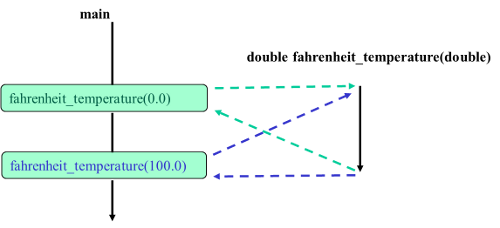 |
| Program: Et program som udskriver en celcius fahrenheit tabel. |
|
| Program: Output fra ovenstående program. |
|
| Eksempel: Antal dage i en måned Slide Indhold Stikord Referencer |
|
| Program: Et program der beregner antal dage i en måned - helt uden funktioner. |
|
| Program: Et program der beregner antal dage i en måned med en funktion - uden IsLeapYear funktionen. |
|
| Program: Et program der beregner antal dage i en måned med en funktion. |
|
|
| Eksempel: GCD Slide Indhold Stikord Referencer |
|
| Program: Et program der beregner største fælles divisor med en funktion. |
|
|
| Opgave 5.5. Find de første n primtal | Denne opgave giver dig blandt andet træning i programmering af et C program, der anvender en header file (.h fil) og en tilhørende .c fil. I denne opgaven kalder vi en funktion, som allerede er skrevet. I senere opgaver skal du selv i gang med at skrive dine funktioner. Du skal skrive et program med en main funktion der udskriver de første n primtal. Skriv dit program i en fil der hedder test-primes.c. Der ønskes følgende output hvis n er 100: prime 1: 2 prime 2: 3 prime 3: 5 prime 4: 7 prime 5: 11 prime 6: 13 prime 7: 17 prime 8: 19 prime 9: 23 prime 10: 29 ... prime 99: 523 prime 100: 541 I din main funktion skal du - ganske enkelt - gennemløbe så mange positive heltal, som det er nødvendigt, for at finde de første n primtal. For at få alt dette til at virke skal du lave følgende primes.h fil: /* Return if i is a prime number */ int is_prime(int i); Endvidere skal du placere følgende programlinier i filen primes.c, og oversætte denne c fil separat. #include "primes.h"
#include <math.h>
#include <assert.h>
/* Return if i is a prime number.
It is assumed as a precondition that the parameter i is non-negative */
int is_prime(int i){
assert(i >= 0);
if (i == 1)
return 0;
else if (i == 2)
return 1;
else if (i % 2 == 0)
return 0;
else{
int k, limit;
limit = (int)(ceil(sqrt(i)));
for (k = 3; k <= limit; k += 2)
if (i % k == 0)
return 0;
return 1;
}
}
Compilering af programmet: Følg mønstret fra vores gennemgang af oversættelse af tændstikpige programmet. Læs og forstå også funktionen is_prime. Inspirationen til denne opgave er fra bogen C by Dissection - anvendt med tilladelse fra forlaget. |
| Opgave 5.5. Goldbachs Formodning | Goldbachs formodning udtrykker en påstand om at alle lige heltal større end to er summen af to primtal. Denne formodning er hverken bevist eller modbevist. I denne opgave vil vi beskæftige os med følgende variation af påstanden:
Skriv et program der beviser denne formodning for alle lige heltal mellem to givne grænser. Eksempelvis for alle lige heltal mellem 7 og 2.000.000. Hvis du er i stand til at finde et modeksempel, er berømmelsen måske lige om hjørnet... Det foreslås at funktionen is_prime fra en tidligere opgave bruges ved løsningen af denne opgave. Det er for stor en mundfuld at løse dette problem uden opdeling i mindre delproblemer. Det foreslås derfor at I skriver en funktion, som undersøger påstanden for et bestemt lige heltal, n. Denne funktion kan så kaldes for alle lige heltal n mellem f.eks. 7 og 2.000.000. Hint: Når I skal bevise påstanden for et tal, n, anbefales det at gennemløbe alle mulige summer (n-i) + i, og dermed undersøge om I kan finde et i så både n-i og i er ulige primtal. Hvis I bliver hurtigt færdige med denne opgave bedes I se på den variant, der på Wikipedia beskrives som Goldbach's weak conjecture. Som en anden udfordring, kan det være interessant at se alle mulige summer- ikke kun den første. Eller denne variant: Hvilket af de testede tal har det største antal opløsninger? Denne opgave stammer fra bogen C by Dissection - anvendt med tilladelse fra forlaget. |
| Opgave 5.5. RGB Pixels | I en tidligere opgave har vi arbejdet med PPM grafik, hvor vi med tre kald af fputc skrev én pixel bestående af tre bytes (rød, grøn, blå) på en fil. Denne opgave forbereder vores fremtidige programmering af PPM grafik med en eksplict og relativ kompakt repræsentation af farverne i én pixel. I denne opgave vil vi repræsentere en pixel i en unsigned int, som antages at fylde 4 bytes, på følgende måde:
Skriv en funktion unsigned int make_pixel(int red, int green, int blue); som indsætter tre heltal (som hver forudsættes at være mellem 0 og 255) i en unsigned int, og returnerer den resulterende pixels (som en unsigned int). Skriv endvidere tre funktioner, som udtrækker hhv. den røde grønne og blå komponent af en pixel: int get_red(unsigned int p); int get_green(unsigned int p); int get_blue(unsigned int p); Det skal naturligvis være således at
Check at dette er tilfældet gennem en række eksempler (såkaldte test - eller 'unit tests'). Organiser de fire funktioner ovenfor i filen pixels.c, og lav en tilsvarende header fil pixels.h. Vær sikker på at du kan oversætte (compilere) filen pixels.c separat. Det er attraktivt - men ikke strengt nødvendigt - at anvende de bitvise operatorer (eksempelvis <<, >> og &). Disse er beskrevet i appendix C, side C-3 i lærebogen (7. udgave). Du kan også overveje at se videoen De Bitvise Operatorer. |
| Regler for overførsel af værdiparametre i C Slide Indhold Stikord Referencer |
|
|
| Begrebet formel parameter: En parameter, som optræder i en funktionsdefinition, kaldes en formel parameter. En formel parameter er et navn. | ||
| Begrebet aktuel parameter: En parameter, som optræder i et kald af en funktion, kaldes en aktuel parameter. En aktuel parameter er et udtryk, som beregnes inden det overføres. |
|
| Eksempel: Rodsøgning (1) Slide Indhold Stikord Referencer |
|
| Figur. En kontinuert funktion f med en rod mellem l og u | 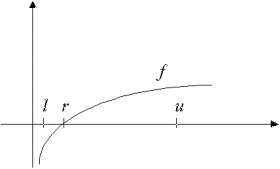 |
|
| Eksempel: Rodsøgning (2) Slide Indhold Stikord Referencer |
| Program: Rodsøgningsfunktionen. |
|
| Program: Funktionerne sameSign, middleOf og isSmallNumber. |
|
| Program: Hele rodsøgningsprogrammet. |
|
|
| Forskellige problemer med input parametre og returværdi Slide Indhold Stikord Referencer |
|
| Program: En double funktion som glemmer at bruge return. |
|
| Program: En void funktion som printer - burde returnere sit resultat. |
|
| Program: En funktion hypotenuse kan ikke se en anden funktions lokale variable. |
|
| Program: Brug af globale variable til input i stedet for parametre. |
|
| Program: Brug af globale variable til input og output. |
|
| Program: Det gode program. |
|
| Programmer og Algoritmer |
| Programmer og Algoritmer Slide Indhold Stikord Referencer |
| Begrebet algoritme: En algoritme er endelig liste af instruktioner til løsning af problem, som karakteriseres af nul, en eller flere input og ét output. Hver instruktion skal være klar, utvetydig, og praktisk gennemførbar for en person som ønsker at følge algoritmen. |
|
|
| Program: Algoritme for løsning af andengradsligning. |
|
| Program: Algoritme som finder største fælles divisor af to ikke-negative heltal - Euclids algoritme. |
|
| Programbeskrivelse og programudførelse Slide Indhold Stikord Referencer |
|
|
| Ekstra Opgaver Slide Indhold Stikord Referencer |
| Opgave 5.8. Skudårsfunktionen | Vi har tidligere i denne lektion mødt skudårsfunktionen int isLeapYear(int year){
int res;
if (year % 400 == 0)
res = 1;
else if (year % 100 == 0)
res = 0;
else if (year % 4 == 0)
res = 1;
else res = 0;
return res;
}
Programmer en ny skudårsfunktion med brug af && og ||, og uden brug af if-else og uden brug af betingede udtryk. Kald begge skudårsfunktioner for alle årstal mellem år 1900 og år 2100. Giver de to funktioner samme resultat på alle årstal? |
| Opgave 5.8. Programmering af en kvadratrodsfunktion | Bibliotektet math.h indholder som bekendt funktionen sqrt, som beregner kvadratroden af et tal i typen double. Programmer din egen kvadratrodsfunktion my_sqrt med brug af Newtons metode. Newtons metode gør det muligt for os at finde denne rod. Se f.eks. denne video (lavet Oscar Veliz) om hvordan dette virker. (Se formlen for rækkeudviklingen ved tid 2:23). Bemærk venligst at forfatteren af videoen laver en fejl i den nederste formel ved tid 2:26. Den korrekte formel er xn+1 = 1/2(xn + a/xn). Regn selv efter. Vær sikker på at du programmerer en funktion, som tager en double som parameter, og som returnerer en double som resultat. Hvordan vil du håndtere en situation, hvor der overføres et negativt input? Udskriv en table over a, my_sqrt(a) og sqrt(a) for alle heltal a mellem 0.0 og 25.0, og check dermed om din nye funktion leverer gode resultater. |
| Opgave 5.8. Nye funktioner i gamle opgaver | I lektionen om iterative kontrolstrukturer arbejdede vi med to opgaver, som vi nu vil tage op igen med det formål at indføre abstraktion med funktioner. I opgave programmeringsopgave 1 side 267 (i Problem Solving and Program Design in C, eighth edition) summerede vi alle heltal fra 1 til n, og vi sammenlignede værdien af denne sum med (n + 1)* n / 2. Skriv nu følgende to funktioner:
I skal kalde disse to funktioner på passende input og sammenligne deres resultater (ligesom i den oprindelige opgave). I lektionen om iterative kontrolstrukturer arbejdede vi også med opgave 1 side 181 i bogen. Vi har en befolkning på 9870 personer som vokser med 10% per år. Spørgsmålet var hvor mange år der går inden befolkningstallet er mere end 30000. Skriv nu en funktion som generaliserer denne opgave. Mere specifikt:
Kald derefter funktionen så den løser opgaven fra side 181 i bogen (med de tre givne tal 9870, 10% og 30000). |
Kapitel 5: Funktioner
Kursets hjemmeside Forfatteren's hjemmeside Om frembringelsen af disse sider Forrige lektion (top) Næste lektion (top) Forrige lektion (bund) Næste lektion (bund)
Genereret: 9. maj 2022, 13:58:59