Probablistic Timed Automata

Kim G. Larsen

In many situations it is useful to refine non-deterministic choice to a probabilistic choice in order to provide more informative model and allow for performance analysis.

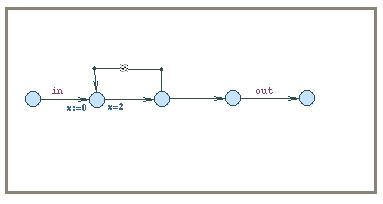
Consider the example to the left. Here a communication medium receive a messeage (in) and after 2 seconds non-deterministically chooses to either go to a state where the message is delivered (out) or to let another 2 seconds pass after which .....  In this model delivery of messages is certainly not guaranteed and it is completely impossible to say anything meaningful about how long time it will take before a message will successfully get through (except that it will take at least 2 seconds).

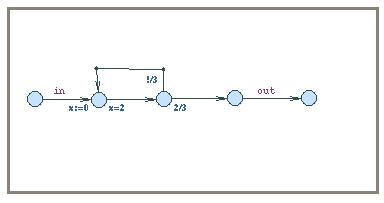A probabilistic refinement of the non-deterministic timed automata could be as shown to the right.  Here a message will be succesfully delivered with probability 2/3 and will require an additional 2 seconds with probability 1/3.  Obviously with this refined model it is meaningful to talk about the expected time before a message gets throuhg (??) and also what the probability is that a message gets through within a given time bound.  Model checking of stochastic models (e.g. Markov Chains) is a hot topic as witnessed by two prominent tools PRISM and RAPTURE.  Stochastic extensions of timed automata is a much need formalism and  the project will involve a variety of topics ranging from formal definition of the model, suitable probabilistic notions of  bisimulation, probabilistic logics, necessary extension of the symbolic techniques existing for timed automata, possible connection to PRISM and/or RAPTURE.  There will here be ample possibility of interacting with collaborators at Twente and Achen University.