Clock-Synchronization and Logical Time

We consider the problem of agreeing on time in a distributed system. Since a distributed systems is defined as one where processes communicate by message passing, we cannot have a single global clock every process refer to in order to tell what time it is. It turns out, that is impossible to have a global notion of time in a distributed systems, so the only thing we can hope for, is to get the processes to agree on the time within a specific bound. However, if we are interested in knowing if some event a happens before some other event b, an approximate agreement on what the time is, is not good enough, and we have to resort to another notion of time, called logical time, which allows us to order causally related events

[DS] Chapter 11.1-11.4

1. [DS] 11.3, 11.4
2. Assign Lamport timestamps to the events in the diagram below. For the given pair of events below, describe wheter the events are related by the
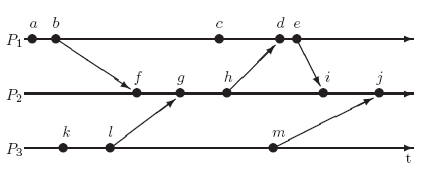
   following relations; →,←, "concurrent" . Do the same using vector clocks.
   (i) f and j
   (ii) a and m
   (iii) c and j
   (iv) k and e
   (v) j and k
   
   
3. Consider a collection of processes that contend for a shared resource (such as a file, printer, etc.). It is important that only one process access the resource at a time, or bad things may happen (inconsistent data in the file, garbled printer output, etc.). Therefore, the processes cooperate by running a mutual exclusion protocol to ensure that at most one process has access to the resource at a given time. There are many different approaches to this problem, but the following one exploits the logical clocks you have just considered.

    

   • Let each process have a unique identifier. (Assume eg that these will be given at the command line on start up.)
   • Let each process maintain a request queue, not seen by any other process. Each queue entry contains the unique identifier of a requesting process and the logical time of the request. The queue is kept in increasing logical time order (i.e., the entry at the head of the queue has the least logical time).
   • To request the resource, a process broadcasts a request message to all other processes.
   • Whenever a process receives a request, it puts the request in its queue and sends an acknowledgement message to the requesting process.
   • A process P can use the resource whenever the following conditions are satisfied:
     1. Process P's own request is at the head of P's request queue.
     2. Process P has received a message (could be an acknowledgement or any other message) from every other process with a logical timestamp (send event time) greater than P's request time.
   • When a process finishes using the resource, it sends a release message to every other process.
   • Whenever a process receives a release message, it removes the sender's request from its request queue.

    

   Convince yourself that the algorithm satisfies the following properties:

    

   Mutual Exclusion (safety):

   No two processes access the resource simultaneoulsy.

   No Starvation (liveness):

   Provided that any process holding the resource will eventually release it, a process that requests the resource will eventually get it. (Furthermore, it can be bypassed at most once by each other process.)

4. 11.7